
উপপাদ্যের প্রয়োগ ও সমাধান
Geometry Theorem Applications
Upapadyer prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
Upapadyer prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications | Upapadyer prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications |Upapadyer prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
প্রশ্নমালা
1 একটি বৃত্তে AC এবং BD দুটি জ্যা M বিন্দুতে ছেদ করে। A ও B এবং C ও D বিন্দুতে স্পর্শকগুলি যথাক্রমে P এবং Q বিন্দুতে ছেদ করে। প্রমাণ কর যে, ∠AMD = 12(∠P + ∠Q).
2 P এবং R কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে বহিঃস্থভাবে O বিন্দুতে ছেদ করে। O বিন্দুগামী একটি সরলরেখা বৃত্তদুটিকে যথাক্রমে T এবং S বিন্দুতে ছেদ করে। প্রমাণ কর যে, PT || RS.
3 দুটি বৃত্ত পরস্পরকে P এবং R বিন্দুতে ছেদ করে। P এবং R বিন্দুগামী APB এবং DRC দুটি সরলরেখা যথাক্রমে প্রথম বৃত্তটিকে A ও D বিন্দুতে এবং দ্বিতীয় বৃত্তটিকে B এবং C বিন্দুতে ছেদ করে। প্রমাণ কর যে, AD || BC.
4 প্রমাণ কর যে কোনো বৃত্তস্থ ত্রিভুজের বহিঃস্থ বৃত্তাংশের তিনটি কোণের সমষ্টি 4 সমকোণের সমান।
5 দুটি সমান বৃত্ত পরস্পরকে A এবং B বিন্দুতে ছেদ করে। B বিন্দুগামী একটি সরলরেখা বড় বৃত্তটিকে যথাক্রমে T এবং R বিন্দুতে ছেদ করে। প্রমাণ কর যে, AT = AR.
6 ABCD একটি বৃত্তস্থ চতুর্ভুজ। বৃত্তের উপর E এমন একটি বিন্দু যে ∠ABC-এর অন্তঃসমদ্বিখণ্ডক BE। প্রমাণ কর যে, ∠ADC-কে DE বহিঃস্থভাবে সমদ্বিখণ্ডিত করে।
7. দুটি বৃত্ত পরস্পরকে A এবং B বিন্দুতে ছেদ করে, এবং একটি বৃত্ত অপরটির কেন্দ্র দিয়ে যায়। প্রথম বৃত্তের উপর P একটি বিন্দু এবং PAQ সরলরেখা অপর বৃত্তটিকে Q বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, PB = PQ।
8 ABCD একটি বৃত্তস্থ চতুর্ভুজ। AB এবং DC-কে বর্ধিত করলে P বিন্দুতে ছেদ করে, আবার, AD এবং BC-কে বর্ধিত করলে R বিন্দুতে ছেদ করে। BCP এবং CDR ত্রিভুজগুলোর বহির্বৃত্ত পরস্পর T বিন্দুতে ছেদ করে। প্রমাণ কর যে, P, T, R বিন্দুগুলি সমরেখ।
9. O কেন্দ্র বিশিষ্ট একটি বৃত্তের QR একটি জ্যা। Q এবং R বিন্দুতে অঙ্কিত স্পর্শকদ্বয় পরস্পরকে P বিন্দুতে ছেদ করে। QM একটি ব্যাস। প্রমাণ কর যে, ∠QPR = 2∠RQM.
10 দুটি বৃত্ত পরস্পরকে P এবং R বিন্দুতে ছেদ করে। P বিন্দু দিয়ে একটি সরলরেখা অঙ্কন করা হল যা বৃত্ত দুটিকে A এবং B বিন্দুতে ছেদ করে। R বিন্দু দিয়ে AB-এর সমান্তরাল একটি সরলরেখা অঙ্কন করা হল, যা বৃত্ত দুটিকে C এবং D বিন্দুতে ছেদ করে। প্রমাণ কর যে, AB = CD.
11. প্রমাণ কর যে কোন ত্রিভুজের বাহুগুলির মধ্যবিন্দুগুলি এবং যেকোনো শীর্ষবিন্দু থেকে বিপরীত বাহুর উপরে লম্বের ছেদবিন্দু সমবৃত্তীয়।
12. A এবং B কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে X এবং Y বিন্দুতে ছেদ করে। AB-এর সমান্তরাল O-এর গামে X বিন্দু যুক্ত করা হলো। XOY রেখা XO-এর অংশ এবং বড় বৃত্তটিকে P এবং Q বিন্দুতে ছেদ করে। প্রমাণ কর যে, PX = XQ.
13. একই বৃত্তের AB এবং AC দুটি সমান জ্যা । প্রমাণ কর যে BAC কোণের সমদ্বিখণ্ডক কেন্দ্রের উপর দিয়ে যায়।
14. ΔABC বৃত্তে অন্তর্লিখিত একটি ত্রিভুজ। A, B এবং C-এর অন্তসমদ্বিখণ্ডকত্রয় AX, BY এবং CZ বৃত্তটির সাথে যথাক্রমে X, Y এবং Z বিন্দুতে মিলিত হয়। প্রমাণ কর যে AX ⊥ YZ, BY ⊥ XZ, CZ ⊥ XY.
15. যে কোনো ত্রিভুজ ABC-এর পরিকেন্দ্র S এবং A বিন্দু থেকে BC বাহুর উপরে AD লম্ব। প্রমাণ কর যে ∠BAS = ∠CAD.
16. প্রমাণ কর যে, কোনো বৃত্তস্থ চতুর্ভুজের বিপরীত বাহুগুলি বর্ধিত করলে যে দুটি কোণ উৎপন্ন হয়, তার সমদ্বিখণ্ডকদ্বয় পরস্পর লম্ব।
17. A এবং B বিন্দুতে ছেদ করে এমন দুটি বৃত্তের দুটি সরল স্পর্শক PQ এবং RS। AB-কে উভাদিকে বর্ধিত করলে তা স্পর্শক PQ এবং RS-কে যথাক্রমে X এবং Y বিন্দুতে ছেদ করে। প্রমাণ কর যে, XY² – AB² = PQ².
18. AB এর AC কোন বৃত্তের উপর অঙ্কিত স্পর্শক। ∆ABC-এর বাইরে বৃত্তের উপর D যে কোন একটি বিন্দু। দেখাও যে, ∠ABD + ∠ACD = ধ্রুবক
19. O কেন্দ্রীয় একটি বৃত্তের PQ একটি জ্যা এবং AB ব্যাস।প্রমাণ কর যে AB-এর যে কোন অবস্থানে A এবং B থেকে PQ-এর উপর অঙ্কিত লম্বের সমষ্টি সর্বদা ধ্রুবক।
20. ABC যে কোন একটি ত্রিভুজ। BQ এবং CP যথাক্রমে AC এবং AB-এর উপরে লম্ব। ABC ত্রিভুজের পরিবৃত্তে A বিন্দুতে AT একটি স্পর্শক। প্রমাণ কর যে, PQ ∥ AT
21. ΔABC বৃত্তে অন্তর্লিখিত একটি সমবাহু ত্রিভুজ। BC বৃত্তচাপের উপর P একটি বিন্দু। প্রমাণ কর যে PA = PB + PC
22. প্রমাণ কর যে কোনো বৃত্তস্থ চতুর্ভুজের কর্ণদ্বয়ের গুণফল বিপরীত বাহুগুলির গুণফলের সমষ্টির সমান।
23 P কেন্দ্রবিশিষ্ট বৃত্তের একটি ব্যাস AB এবং C পরিধিস্থ যে কোনো একটি বিন্দু। C বিন্দুতে বৃত্তটির স্পর্শক, A এবং B বিন্দুতে অঙ্কিত স্পর্শক দুটিকে যথাক্রমে Q এবং R বিন্দুতে ছেদ করে। প্রমাণ কর যে, ∠QPR = 90°
24. P এবং Q কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে বহিস্থঃভাবে A বিন্দুতে স্পর্শ করে। RS বৃত্তদুটির সরল সাধারণ স্পর্শক R এবং S যথাক্রমে বৃত্তদুটির পরিধিস্থ বিন্দু। প্রমাণ কর যে
(i) A বিন্দুতে অঙ্কিত তির্যক স্পর্শক RS-কে সমদ্বিখণ্ডিত করে।
(ii) ∠PTQ = 90° (iii) ∠RAS = 90°
25. প্রমাণ কর যে, বহিঃস্থভাবে স্পর্শ করে এমন দুটি বৃত্তের সরল সাধারণ স্পর্শকের দৈর্ঘ্যের বর্গ বৃত্তদুটির ব্যাসার্ধের গুণফলের চার গুণ।
26. O কেন্দ্রবিশিষ্ট একটি বৃত্তের দুটি জ্যা AC এবং BD পরস্পরকে P বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, ∠APB = 12(∠AOB +∠COD)
27. কোনো বৃত্তের পরিলিখিত চতুর্ভুজের যে কোনো দুটি বিপরীত বাহুর সমষ্টি অপর দুটি বিপরীত বাহুর সমষ্টির সমান।
28. CD সরলরেখা একটি বৃত্তকে A এবং B বিন্দুতে এমনভাবে ছেদ করে যে, AC = BD হয়। C এবং D বিন্দু দিয়ে বৃত্তটির দুটি স্পর্শক অঙ্কন করলে বৃত্তটিকে E এবং F বিন্দুতে স্পর্শ করে। প্রমাণ কর যে, AB জ্যাকে EF সমদ্বিখণ্ডিত করে।
29. কোনো বৃত্তের দুটি ব্যাস AB ও CD পরস্পরের উপর লম্ব। AC বৃত্তচাপের উপর P একটি যে কোনো বিন্দু। প্রমাণ কর যে PB2 – PA2 = 4 PCD
30 ABC ত্রিভুজের শীর্ষবিন্দু G। AC-কে বর্ধিত করা হলো যা BC-কে O বিন্দুতে ছেদ করে। ত্রিভুজটির বহিঃবৃত্তকে D বিন্দুতে ছেদ করে। প্রমাণ কর যে, GO = DO
31 ABC ত্রিভুজের ∠A-এর সমদ্বিখন্ডক BC-কে D বিন্দুতে ছেদ করে এবং ত্রিভুজটির বহিঃবৃত্তকে E বিন্দুতে ছেদ করে। প্রমাণ কর যে, AB.AC = AD.AE
32 ABCD একটি বৃত্তস্থ চতুর্ভুজ। BD কর্ণ AC কর্ণকে সমদ্বিখন্ডিত করে। দেখাও যে, AB.AD = CB.CD
33 যে ট্রাপিজিয়ামের সমান্তরাল বাহুগুলির অনুপাত 1 : 2, প্রমাণ কর যে তার কর্ণগুলি পরস্পরকে এক-তৃতীয়াংশে বিভক্ত করে।
34 একটি বৃত্তের দুটি সমান জ্যা CA এবং CB। BA-কে যেকোনো বিন্দু P পর্যন্ত বর্ধিত করা হল। CP যুক্ত করা হলে, বৃত্তের T বিন্দুতে ছেদ করে। প্রমাণ কর যে, (i) ∠CAT = ∠TPA (ii) CA.CB = CP.CT
35 ABC যেকোনো একটি ত্রিভুজের BC বাহুর উপর D যেকোনো একটি বিন্দু। AD যুক্ত করা হল। B এবং C বিন্দুতে AD-এর সমান্তরাল BR এবং CT অঙ্কন করা হল, BA এবং CA-কে বর্ধিত করা হল, যা সমান্তরাল বাহুদ্বয়কে যথাক্রমে T এবং R বিন্দুতে ছেদ করে। প্রমাণ কর যে, 1AD = 1RB + 1TC
36 ABC ত্রিভুজের ভূমি BC-এর মধ্যবিন্দু M দিয়ে DME একটি সরলরেখা এমনভাবে অঙ্কন করা হল, যাতে তা AB এবং বর্ধিত AC থেকে দুটি সমান অংশ AD এবং AE কেটে নেয়। প্রমাণ কর যে, BD = CE
37 ABCD একটি ট্রাপিজিয়াম এর AC এবং BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে। তির্যক বাহুদ্বয় DA এবং CB কে বর্ধিত করলে P বিন্দুতে ছেদ করে। প্রমাণ কর যে, AB-কে PO সমদ্বিখন্ডিত করে।
38 ABCD এবং AECF দুটি সামান্তরিক এবং EF ও AD পরস্পর সমান্তরাল। যদি AF ও DE ছেদ করে G বিন্দুতে এবং BF ও CE ছেদ করে H বিন্দুতে, তবে প্রমাণ কর যে, GH || AB.
39 PQR ত্রিভুজে PQ = PR। PQ-এর মধ্যবিন্দু S এবং PQ-এর লম্ব সমদ্বিখন্ডক ভূমি QR-এর বর্ধিতাংশকে T বিন্দুতে ছেদ করে। প্রমাণ কর যে, PQ² = QR.QT.
40 ABCD একটি রম্বস। C বিন্দু দিয়ে অঙ্কিত সরলরেখা AD-কে P বিন্দুতে এবং বর্ধিত AB-কে Q বিন্দুতে ছেদ করে। যদি DP = 12 AB হয়, দেখাও যে, BQ = 2AB.
41 ABCD একটি সামান্তরিকের BC এবং CD বাহুর মধ্যবিন্দু P এবং Q। AP এবং AQ রেখাংশ কর্ণ BD-কে যথাক্রমে K এবং L বিন্দুতে ছেদ করে। প্রমাণ কর যে BK = KL = LD = 13 BD
42 একটি সমকোণী ত্রিভুজের বাহুগুলি ক্রমিক সমানুপাতী হলে এবং তার সমকোণ থেকে অতিভুজের উপর লম্ব অঙ্কন করা হলে, দেখাও যে অতিভুজের বৃহত্তম অংশটি ত্রিভুজের ক্ষুদ্রতম বাহুর সমান।
43 ABCD একটি সামান্তরিক, AD-এর সামান্তরাল সরলরেখার উপর E এবং F দুটি বিন্দু। AE, DF-কে বর্ধিত করলে
তা P বিন্দুতে এবং BE, CF-কে বর্ধিত করলে তা Q বিন্দুতে ছেদ করে। প্রমাণ কর যে, PQ || AB.
44 ABC সমকোণী ত্রিভুজের ∠A সমকোণ, BC অতিভুজের উপর AD লম্ব প্রমাণ কর যে, ΔABCΔACD = BC2AC2
45 প্রমাণ কর যে, কোন ত্রিভুজের শীর্ষবিন্দু থেকে লম্ববিন্দুর দৈর্ঘ্য শীর্ষবিন্দুর বিপরীত বাহু থেকে পরিকেন্দ্রের দৈর্ঘ্যের দ্বিগুণ।
46 APB বৃত্তের P বিন্দু থেকে অঙ্কিত লম্ব ব্যাস AB কে N বিন্দুতে ছেদ করে। প্রমাণ কর যে, PB² = AB.NB.
47 একটি বৃত্তের ব্যাস AB, AP এবং AQ জ্যা দুটির বর্ধিত করলে B বিন্দুতে অঙ্কিত স্পর্শককে তারা যথাক্রমে X এবং Y বিন্দুতে ছেদ করে, দেখাও যে,
(i) APQ এবং AXY ত্রিভুজদ্বয় অনুরূপ (ii) P, Q, Y, X বিন্দু চারটি সমবৃত্তস্থ
Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
সমাধান
1 একটি বৃত্তে AC এবং BD দুটি জ্যা M বিন্দুতে ছেদ করে। A ও B এবং C ও D বিন্দুতে স্পর্শকগুলি যথাক্রমে P এবং Q বিন্দুতে ছেদ করে। প্রমাণ কর যে, ∠AMD = 12(∠P + ∠Q).
অঙ্কনঃ বৃত্তের কেন্দ্র O থেকে OA, OB, OC, OD অঙ্কন করা হল এবং CD যুক্ত করা হল।
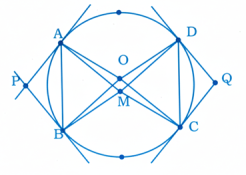 প্রমাণঃ MCD ত্রিভুজে, বহিস্থ ∠AMD অন্তঃস্থ বিপরীত কোণ দুটির সমষ্টির সমান।
প্রমাণঃ MCD ত্রিভুজে, বহিস্থ ∠AMD অন্তঃস্থ বিপরীত কোণ দুটির সমষ্টির সমান।
∴ ∠AMD = ∠MDC + ∠MCD
= ½ ∠BOC + ½ ∠AOD [∵ একই চাপের উপর কেন্দ্রস্থ কোণ পরিধিস্ত কোণের দ্বিগুণ]
= ½ [∠BOC + ∠AOD]
= ½ [360° – ∠AOB – ∠COD]
= ½ [360° – (180° – ∠APB) – (180° – ∠CQD)]
[যেহেতু APBO চতুর্ভুজ, ∠OAP = ∠OBP = 90° যেহেতু ব্যাসার্ধ স্পর্শকের উপর লম্ববিন্দুতে লম্ব হয়।
∴ ∠AOB + ∠APB = 180° অনুরূপভাবে, ODQC চতুর্ভুজে, ∠COD + ∠CQD = 180°]
= ½ [360° – 180° + ∠APB – 180° + ∠CQD]
= ½ [∠APB + ∠CQD] (প্রমাণিত)
2 P এবং R কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে বহিঃস্থভাবে O বিন্দুতে ছেদ করে। O বিন্দুগামী একটি সরলরেখা বৃত্তদুটিকে যথাক্রমে T এবং S বিন্দুতে ছেদ করে। প্রমাণ কর যে, PT || RS.
প্রমাণঃ POT ত্রিভুজে, PO = OT (একই বৃত্তের ব্যাসার্ধ)
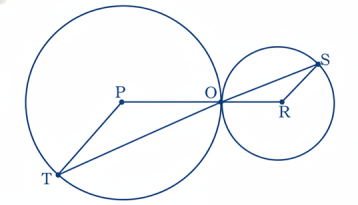 ∴ ∠POT = ∠PTO
∴ ∠POT = ∠PTO
আবার, ROS ত্রিভুজে, RO = RS (একই বৃত্তের ব্যাসার্ধ)
∴ ∠ROS = ∠RSO
কিন্তু ∠POT = ∠ROS (∵বিপ্রতীপ কোণ)
∴ ∠PTO = ∠RSO
কিন্তু এরা একান্তর কোণ
∴ PT || RS (প্রমাণিত)
3 দুটি বৃত্ত পরস্পরকে P এবং R বিন্দুতে ছেদ করে। P এবং R বিন্দুগামী APB এবং DRC দুটি সরলরেখা যথাক্রমে প্রথম বৃত্তটিকে A ও D বিন্দুতে এবং দ্বিতীয় বৃত্তটিকে B এবং C বিন্দুতে ছেদ করে। প্রমাণ কর যে, AD || BC.
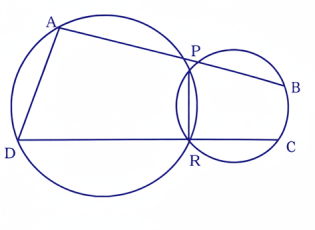 অঙ্কনঃ AD, BC এবং PR যুক্ত করা হল।
অঙ্কনঃ AD, BC এবং PR যুক্ত করা হল।
প্রমাণঃ APRD একটি বৃত্তস্থ চতুর্ভুজ।
∴ ∠DAP + ∠DRP = 2 সমকোণ
আবার, BPRC একটি বৃত্তস্থ চতুর্ভুজ
∴ ∠PBC + ∠PRC = 2 সমকোণ
∴ যোগ করে,
∠DAP + ∠DRP + ∠PBC + ∠PRC = 4 সমকোণ
∴ ∠DAP + ∠PBC + (∠DRP + ∠PRC) = 4 সমকোণ
∴ ∠DAP + ∠PBC + (2 সমকোণ) = 4 সমকোণ
[∵ ∠DRP + ∠PRC = সরল ∠DRC = 2 সমকোণ]
∴ ∠DAP + ∠PBC = 2 সমকোণ
অর্থাৎ, ∠DAB + ∠ABC = 2 সমকোণ
∴ AD || BC (প্রমাণিত)
4 প্রমাণ কর যে কোনো বৃত্তস্থ ত্রিভুজের বহিঃস্থ বৃত্তাংশের তিনটি কোণের সমষ্টি 4 সমকোণের সমান।
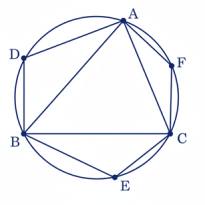
কল্পনাঃ বৃত্তস্থ একটি ত্রিভুজ ABC
ABC ত্রিভুজের বহিঃস্থ তিনটি বৃত্তাংশে তিনটি কোণ
∠ADB, ∠BEC এবং ∠CFA
প্রমাণ করতে হবে
∠ADB + ∠BEC + ∠CFA = 4 সমকোণ
প্রমাণঃ যেহেতু বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলির সমষ্টি 2 সমকোণ।
∠ADB + ∠ACB = 2 সমকোণ
অনুরূপভাবে, ∠BAC + ∠BEC = 2 সমকোণ [∵ABEC একটি বৃত্তস্থ চতুর্ভুজ]
এবং ∠CFA + ∠ABC = 2 সমকোণ
∴যোগ করে,
∠ADB + ∠ACB + ∠BEC + ∠BAC + ∠CFA + ∠ABC = 6 সমকোণ
অর্থাৎ, (∠ADB + ∠BEC + ∠CFA) + (∠ACB + ∠BAC + ∠ABC) = 6 সমকোণ
কিন্তু ABC ত্রিভুজে, ∠ACB + ∠BAC + ∠ABC = 2 সমকোণ
∴ ∠ADB + ∠BEC + ∠CFA = 4 সমকোণ (প্রমাণিত)
5 দুটি সমান বৃত্ত পরস্পরকে A এবং B বিন্দুতে ছেদ করে। B বিন্দুগামী একটি সরলরেখা বড় বৃত্তটিকে যথাক্রমে T এবং R বিন্দুতে ছেদ করে। প্রমাণ কর যে, AT = AR.
অঙ্কনঃ A এবং B কেন্দ্র দুটি যথাক্রমে P এবং Q। PA, PB, QA, QB যুক্ত করা হল।
প্রমাণঃ PA = PB (∵ একই বৃত্তের ব্যাসার্ধ)
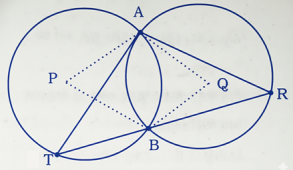 QA = QB (∵ একই বৃত্তের ব্যাসার্ধ)
QA = QB (∵ একই বৃত্তের ব্যাসার্ধ)
∴ PA = PB = QA = QB (∵ দুটি বৃত্ত সমান)
∴ □APBQ একটি রম্বস (∵ চারটি বাহুই সমান)
∴ ∠APB = ∠AQB (∵ রম্বসের বিপরীত কোণগুলি সমান)
এখন, যেহেতু কোনো বৃত্তে একই চাপ দ্বারা গঠিত বৃত্তস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ
∴ ∠APB = 2∠ATB এবং ∠AQB = 2∠ARB
∴ ∠ATB = ∠ARB
∴ AT = AR [∵ ART ত্রিভুজে, দুটি কোণ সমান] (প্রমাণিত)
6 ABCD একটি বৃত্তস্থ চতুর্ভুজ। বৃত্তের উপর E এমন একটি বিন্দু যে ∠ABC-এর অন্তঃসমদ্বিখণ্ডক BE। প্রমাণ কর যে, ∠ADC-কে DE বহিঃস্থভাবে সমদ্বিখণ্ডিত করে।
অঙ্কনঃ CD-কে F পর্যন্ত বর্ধিত করা হল।
প্রমাণঃ যেহেতু ABCD বৃত্তস্থ চতুর্ভুজ।
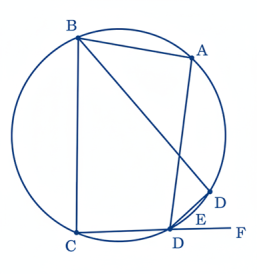
∴ ∠ABC + ∠ADC = 2 সমকোণ
আবার, ∠ADF + ∠ADC = 2 সমকোণ
∴ ∠ABC + ∠ADC = ∠ADF + ∠ADC
∴∠ABC = ∠ADF
কিন্তু ∠ABC = 2 ∠ABE [∵ ∠ABC-এর অন্তরসমদ্বিখণ্ডক BE]
∴ 2 ∠ABE = ∠ADF
এখন, ∠ABE = ∠ADE
∴ 2∠ADE = ∠ADF
অর্থাৎ, ∠ADF-এর সমদ্বিখণ্ডক DE
অতএব, ∠ADC-এর বহিঃসমদ্বিখণ্ডক DE (প্রমাণিত)
7. দুটি বৃত্ত পরস্পরকে A এবং B বিন্দুতে ছেদ করে, এবং একটি বৃত্ত অপরটির কেন্দ্র দিয়ে যায়। প্রথম বৃত্তের উপর P একটি বিন্দু এবং PAQ সরলরেখা অপর বৃত্তটিকে Q বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, PB = PQ।
অঙ্কনঃOA, OB, PB এবং QB যুক্ত করা হল।
প্রমাণঃপ্রথম বৃত্তটি দ্বিতীয় বৃত্তের কেন্দ্র O দিয়ে যায়।
এখন, দ্বিতীয় বৃত্তে, ∠AOB = 2∠AQB অর্থাৎ, 2∠PQB
[∵ একই চাপ দ্বারা গঠিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ]
আবার, যেহেতু PAOB একটি বৃত্তস্থ চতুর্ভুজ
∴ ∠BPA + ∠AOB = 180° ……… (i)
কিন্তু PBQ ত্রিভুজে,
∠PBQ + ∠PQB + ∠BPQ = 180° ……… (ii)
∴ (i) এবং (ii) তুলনা করে,
∠PBQ + ∠PQB + ∠BPQ = ∠BPA + ∠AOB
বা, ∠PBQ + ∠PQB + ∠BPQ = ∠BPQ + 2∠PQB
∴ ∠PBQ = ∠PQB
∴ PB = PQ (প্রমাণিত)
8 ABCD একটি বৃত্তস্থ চতুর্ভুজ। AB এবং DC-কে বর্ধিত করলে P বিন্দুতে ছেদ করে, আবার, AD এবং BC-কে বর্ধিত করলে R বিন্দুতে ছেদ করে। BCP এবং CDR ত্রিভুজগুলোর বহির্বৃত্ত পরস্পর T বিন্দুতে ছেদ করে। প্রমাণ কর যে, P, T, R বিন্দুগুলি সমরেখ।
অঙ্কনঃ CT যুক্ত করা হল।
প্রমাণঃ যেহেতু BCTP একটি বৃত্তস্থ চতুর্ভুজ।
∴ ∠PTC + ∠PBC = 180°
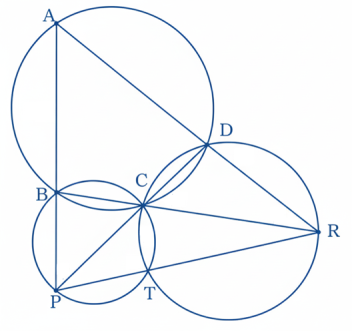 [∵ ∠ABC + ∠PBC = 180°]
[∵ ∠ABC + ∠PBC = 180°]
∴ ∠PTC = 180° – ∠PBC = ∠ABC
আবার, DRTC একটি বৃত্তস্থ চতুর্ভুজ।
∴ ∠CTR + ∠CDR = 180°
∴ ∠CTR = 180° – ∠CDR = ∠ADC
[∵∠ADC + ∠CDR = 180°
অতএব, যোগ করে,
∠PTC + ∠CTR = ∠ABC + ∠ADC
কিন্তু ∠ABC + ∠ADC = 180° [∵ ABCD একটি বৃত্তস্থ চতুর্ভুজ]
∴ ∠PTC + ∠CTR = ∠PTR = 180°, অর্থাৎ, সরল কোণ
∴ P, T, R বিন্দুগুলি সমরেখ। (প্রমাণিত)
9. O কেন্দ্র বিশিষ্ট একটি বৃত্তের QR একটি জ্যা। Q এবং R বিন্দুতে অঙ্কিত স্পর্শকদ্বয় পরস্পরকে P বিন্দুতে ছেদ করে। QM একটি ব্যাস। প্রমাণ কর যে, ∠QPR = 2∠RQM.
পদ্ধতি 1
প্রমাণঃ যেহেতু O কেন্দ্রবিশিষ্ট বৃত্তের বহিস্থ P বিন্দু থেকে PQ এবং PR দুটি স্পর্শক
∴ স্পর্শক দুটির দৈর্ঘ্য সমান।
∴ PQ = PR
∴ ∠PQR = ∠PRQ
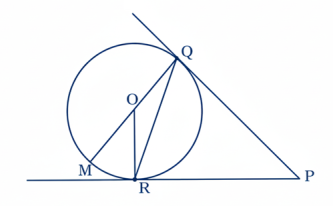 অতএব, PQR ত্রিভুজে,
অতএব, PQR ত্রিভুজে,
∠QPR + ∠PQR + ∠PRQ = 180°
∴ ∠QPR + ∠PQR+ ∠PQR = 180°
∴ ∠QPR + 2∠PQR = 180° ………. (i)
আবার, QM ⊥ QP, যেহেতু স্পর্শকের ছেদবিন্দুতে ব্যাস লম্ব হয়।
∴∠MQP = 90°
∴ 2∠PQR + 2∠RQM = 180° ……… (ii)
অতএব (i) এবং (ii) থেকে,
∠QPR + 2∠PQR = 2∠PQR + 2∠RQM
∴ ∠QPR = 2∠RQM (প্রমাণিত)
পদ্ধতি 2
অঙ্কনঃ OR যুক্ত করা হল।
প্রমাণঃ ∴ ∠OQP = 1 সমকোণ এবং ∠ORP = 1 সমকোণ
[যেহেতু, স্পর্শকের ছেদবিন্দুতে ব্যাসার্ধ লম্ব হয়।]
∴ ∠OQP + ∠ORP = 2 সমকোণ
∴ ∠QOR + ∠QPR = 2 সমকোণ ………. (i)
কিন্তু ∠MOR + ∠QOR = 2 সমকোণ ………. (ii)
∴ ∠QPR + ∠QOR = ∠MOR + ∠QOR
∴ ∠QPR = ∠MOR
কিন্তু ∠MOR = ∠RQM [∵ একই চাপ দ্বারা গঠিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ]
অতএব, ∠QPR = ∠MOR = 2∠RQM (প্রমাণিত)
Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
10 দুটি বৃত্ত পরস্পরকে P এবং R বিন্দুতে ছেদ করে। P বিন্দু দিয়ে একটি সরলরেখা অঙ্কন করা হল যা বৃত্ত দুটিকে A এবং B বিন্দুতে ছেদ করে। R বিন্দু দিয়ে AB-এর সমান্তরাল একটি সরলরেখা অঙ্কন করা হল, যা বৃত্ত দুটিকে C এবং D বিন্দুতে ছেদ করে। প্রমাণ কর যে, AB = CD.
অঙ্কনঃ X এবং Y কেন্দ্র দুটি দিয়ে LM এবং ST দুটি সরলরেখা অঙ্কন করা হল, যে দুটি AB এবং CD সমান্তরাল সরলরেখার উপর লম্ব।
প্রমাণঃ যেহেতু AB || CD (কল্পনা অনুসারে)
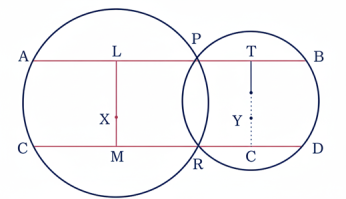 বৃত্তটির কেন্দ্র X দিয়ে AB এবং CD-এর উপরে LM লম্ব। যেহেতু বৃত্তের কেন্দ্র দিয়ে জ্যা-এর উপরে অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে।
বৃত্তটির কেন্দ্র X দিয়ে AB এবং CD-এর উপরে LM লম্ব। যেহেতু বৃত্তের কেন্দ্র দিয়ে জ্যা-এর উপরে অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে।
∴ AP কে XL, সমদ্বিখণ্ডিত করে। অর্থাৎ, LP = ½ AP
এবং CR-কে XM সমদ্বিখণ্ডিত করে। অর্থাৎ, MR = ½ CR
অনুরূপভাবে PT = ½ PB এবং RS = ½ RD
অতএব, LP + PT = ½ AP + ½ PB = ½ (AP + PB)
∴ LT = ½ AB
এবং MR + RS = ½ CR + ½ RD
= ½ (CR + RD)
∴ MS = ½ CD
কিন্তু LT = MS [∵ MLTS আয়তক্ষেত্রের বিপরীত বাহু]
∴ ½ AB = ½ CD
∴ AB = CD (প্রমাণিত)
11. প্রমাণ কর যে কোন ত্রিভুজের বাহুগুলির মধ্যবিন্দুগুলি এবং যেকোনো শীর্ষবিন্দু থেকে বিপরীত বাহুর উপরে লম্বের ছেদবিন্দু সমবৃত্তীয়।
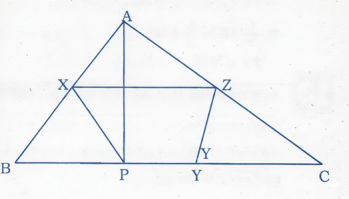 কল্পনাঃ ABC একটি ত্রিভুজ। AB, BC, CA বাহুর মধ্যবিন্দু যথাক্রমে X, Y, Z। A থেকে BC-এর উপরে লম্বের পাদবিন্দু P। প্রমাণ করতে হবে যে X, P, Y, Z সমবৃত্তস্থ।
কল্পনাঃ ABC একটি ত্রিভুজ। AB, BC, CA বাহুর মধ্যবিন্দু যথাক্রমে X, Y, Z। A থেকে BC-এর উপরে লম্বের পাদবিন্দু P। প্রমাণ করতে হবে যে X, P, Y, Z সমবৃত্তস্থ।
অঙ্কনঃ XP এবং YZ যুক্ত করা হল। XZ || BC
[∵ AB- এবং AC-এর মধ্যবিন্দু এর মধ্যবিন্দু X এবং Z]
ZY || AB [∵ AC-এর মধ্যবিন্দু Z এবং BC-এর মধ্যবিন্দু Y]
প্রমাণঃ ত্রিভুজ ZBYX একটি সামান্তরিক
(∵ বিপরীত বাহুগুলি সমান্তরাল)
∴ ∠XBY = ∠XZY (সামান্তরিকের বিপরীত কোণ) …….. (i)
এখন, ABP ত্রিভুজে, AB-এর মধ্যবিন্দু X এবং ∠APB = 90°
∴ PX = ½ AB (∵ সমকোণ হতে, মধ্যমা অতিভুজের অর্ধেক)
অর্থাৎ, PX = XB ∴ ∠XBP = ∠XPB ………. (ii)
(i) এবং (ii) থেকে
∠XZY = ∠XPB
∴ ∠XZY + ∠XPY = ∠XPB + ∠XPY = 180°
∴ ∠XPYZ চতুর্ভুজের বিপরীত কোণগুলির সমষ্টি 180°
∴ চতুর্ভুজটি বৃত্তস্থ অর্থাৎ, X, P, Y, Z বিন্দুগুলি সমবৃত্তস্থ (প্রমাণিত)
12. A এবং B কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে X এবং Y বিন্দুতে ছেদ করে। AB-এর সমান্তরাল O-এর গামে X বিন্দু যুক্ত করা হলো। XOY রেখা XO-এর অংশ এবং বড় বৃত্তটিকে P এবং Q বিন্দুতে ছেদ করে। প্রমাণ কর যে, PX = XQ.
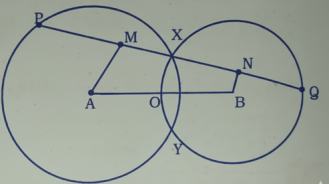 অঙ্কনঃ OX এবং OY যোগ করা হল। AB এবং O-এর সমান্তরাল AM এবং BN অঙ্কন করা হল PQ কে যথাক্রমে M এবং N বিন্দুতে ছেদ করে।
অঙ্কনঃ OX এবং OY যোগ করা হল। AB এবং O-এর সমান্তরাল AM এবং BN অঙ্কন করা হল PQ কে যথাক্রমে M এবং N বিন্দুতে ছেদ করে।
প্রমাণঃ যেহেতু AM || OX || BN (অঙ্কন অনুসারে) এবং AB ও MN ছেদক এবং যেহেতু OA=OB
∴ MX = XN
আবার, PQ –এর উপর AM এবং BN লম্ব
[∵ AM || BN || OX এবং OX ⊥ PQ]
অর্থাৎ, AM ⊥ BN এবং BN ⊥ XQ
[∵ PX এবং XQ একই সরলরেখা PQ এর অংশ]
এখন যেহেতু কেন্দ্র দিয়ে জ্যা-এর উপর অঙ্কিত লম্ব জ্যাকে সমদ্বিখণ্ডিত করে। অতএব PX কে AM এবং XQ কে BN সমদ্বিখণ্ডিত করে।
অর্থাৎ, MX = ½ PX এবং XN = ½ XQ
যেহেতু আগেই প্রমাণিত MX = XN
∴ ½ PX = ½ XQ
∴ PX = XQ (প্রমাণিত)
13. একই বৃত্তের AB এবং AC দুটি সমান জ্যা । প্রমাণ কর যে BAC কোণের সমদ্বিখণ্ডক কেন্দ্রের উপর দিয়ে যায়।
কল্পনাঃ ধরা যাক, ∠BAC-কে AP সমদ্বিখণ্ডিত করে এবং P পরিধির উপর একটি বিন্দু।
BP এবং CP যুক্ত করা হল।
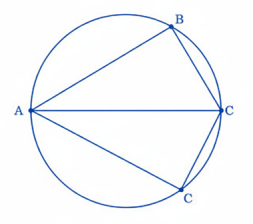 প্রমাণঃ ABP এবং ACP ত্রিভুজের
প্রমাণঃ ABP এবং ACP ত্রিভুজের
AB = AC (কল্পনা অনুসারে) AP সাধারণ বাহু
∠BAP = ∠CAP (∵ ∠BAC-এর সমদ্বিখণ্ডক AP)
∴ ∠ABP = ∠ACP ∴ ত্রিভুজদ্বয় সর্বসম
যেহেতু বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি সম্পূরক
∴ ∠ABP + ∠ACP = 180°
এখন যেহেতু ∠ABP পরিধিস্থ কোণ
∴ AP ব্যাস
∴ AP কেন্দ্রের উপর দিয়ে যায় (প্রমাণিত)
14. ΔABC বৃত্তে অন্তর্লিখিত একটি ত্রিভুজ। A, B এবং C-এর অন্তসমদ্বিখণ্ডকত্রয় AX, BY এবং CZ বৃত্তটির সাথে যথাক্রমে X, Y এবং Z বিন্দুতে মিলিত হয়। প্রমাণ কর যে AX ⊥ YZ, BY ⊥ XZ, CZ ⊥ XY.
প্রমাণঃ XOY ত্রিভুজে,
∠XOY + ∠OYX + ∠OXY = 180°
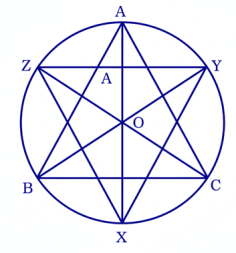 বা, ∠XOY + ∠OYB + ∠BYX + ∠ABY = 180°
বা, ∠XOY + ∠OYB + ∠BYX + ∠ABY = 180°
বা, ∠XOY + ∠ZCB + ∠BAX + ∠ABY = 180°
বা, ∠XOY + ∠C2 + ∠A2 + ∠B2 = 180°
বা, ∠XOY + ∠A + ∠B + ∠C2 = 180°
বা, ∠XOY + 90° = 180°
বা, ∠XOY = 90° অর্থাৎ AX ⊥ YZ
আনুরুপভাবে, BY ⊥ XZ এবং CZ ⊥ XY (প্রমাণিত)
15. যে কোনো ত্রিভুজ ABC-এর পরিকেন্দ্র S এবং A বিন্দু থেকে BC বাহুর উপরে AD লম্ব। প্রমাণ কর যে ∠BAS = ∠CAD.
অঙ্কনঃ AS-কে বৃত্তের উপরিস্থিত P বিন্দু পর্যন্ত বর্ধিত করে BP যুক্ত করা হল।
প্রমাণঃ AP যেহেতু পরিবৃত্তের কেন্দ্র S বিন্দুগামী, অতএব AP বৃত্তের ব্যাস।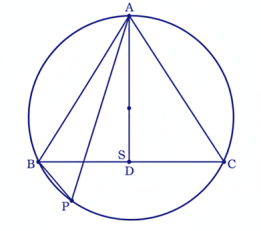
এখন ABP এবং ACD ত্রিভুজদ্বয়ের মধ্যে,
∠ABP = ∠ADC (= 90°)
∠APB = ∠ACD (একই বৃত্তাংশস্থিত কোণ)
অবশিষ্ট ∠BAP = ∠CAD
অর্থাৎ ∠BAS = ∠CAD (প্রমাণিত)
16. প্রমাণ কর যে, কোনো বৃত্তস্থ চতুর্ভুজের বিপরীত বাহুগুলি বর্ধিত করলে যে দুটি কোণ উৎপন্ন হয়, তার সমদ্বিখণ্ডকদ্বয় পরস্পর লম্ব।
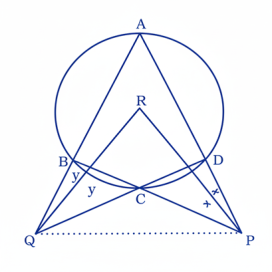 ABCD একটি বৃত্তস্থ চতুর্ভুজ। AD এবং BC-কে বর্ধিত করা হলে তারা P বিন্দুতে ছেদ করে। আবার, AB এবং DC-কে বর্ধিত করলে তারা Q বিন্দুতে ছেদ করে। ∠CPD এবং ∠BQC কোণের সমদ্বিখণ্ডকদ্বয় R বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে ∠PRQ = 90°
ABCD একটি বৃত্তস্থ চতুর্ভুজ। AD এবং BC-কে বর্ধিত করা হলে তারা P বিন্দুতে ছেদ করে। আবার, AB এবং DC-কে বর্ধিত করলে তারা Q বিন্দুতে ছেদ করে। ∠CPD এবং ∠BQC কোণের সমদ্বিখণ্ডকদ্বয় R বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে ∠PRQ = 90°
এখন, ধরা যাক ∠CPQ = w, ∠CQP = z, ∠APR = ∠CPR = x, ∠BQR = ∠CQR = y. PQ যুক্ত করা হল।
প্রমাণঃ ∵ ABCD একটি বৃত্তস্থ চতুর্ভুজ।
∠BAD + ∠BCD = 180°
বা, ∠BCD = 180° – ∠BAD
∴ ∠PCQ = বিপ্রতিপ ∠BCD = 180° – ∠BAD
PCQ ত্রিভুজে, ∠PCQ + ∠CPQ + ∠CQP = 180°
∴ 180° – ∠BAD + ∠CPQ + ∠CQP = 180°
বা, ∠BAQ = ∠CPQ + ∠CQP = w + z
APQ ত্রিভুজে, ∠A + (2y + z) + (2x + w) = 180°
∴ (w + z) + (2y + z) + (2x + w) = 180°
∴ 2x + 2y + 2z + 2w = 180°
∴ x + y + z + w = 90°
∴ ∠A = 90° (প্রমাণিত)
Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
17. A এবং B বিন্দুতে ছেদ করে এমন দুটি বৃত্তের দুটি সরল স্পর্শক PQ এবং RS। AB-কে উভাদিকে বর্ধিত করলে তা স্পর্শক PQ এবং RS-কে যথাক্রমে X এবং Y বিন্দুতে ছেদ করে। প্রমাণ কর যে, XY² – AB² = PQ².
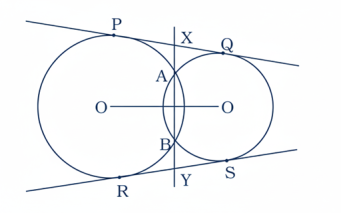 প্রমাণঃ এখানে এটি পরিষ্কার যে, PQ = RS
প্রমাণঃ এখানে এটি পরিষ্কার যে, PQ = RS
PX = XQ = RY = YS
AX = BY
∴ AX + AB = BY + AB
অর্থাৎ, AY = BX
এখন, XY² – AB²
= (AY + AY)² – (BX – AX)² = (AX + BX)² – (BX – AX)²
= (AX² + BX² + 2AX.BX) – (BX² + AX² – 2AX.BX)
= 4AX.BX
= 4.PX² [∵ PX স্পর্শক এবং BX রেখাংশ বৃত্তকে A এবং B বিন্দুতে ছেদ করে]
= (2PX) ²
= PQ² (প্রমাণিত)
18. AB এর AC কোন বৃত্তের উপর অঙ্কিত স্পর্শক। ∆ABC-এর বাইরে বৃত্তের উপর D যে কোন একটি বিন্দু। দেখাও যে, ∠ABD + ∠ACD = ধ্রুবক
প্রমাণঃ ধরা যাক, ∆ABC-এর বাইরে বৃত্তের উপর D-এর আর একটি অবস্থান D’
∴∠BDC = ∠BD’C [∵একই চাপ দ্বারা একই অংশে গঠিত কোণ]
∠BDC + ∠BAC = ∠BD’C + ∠BAC = ধ্রুবক
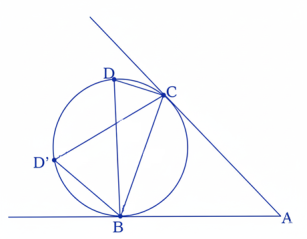
[অর্থাৎ D-এর যে কোন অবস্থানের জন্য সমান]
এখন ABCD চতুর্ভুজে
∠BDC + ∠BAC + ∠ABD + ∠ACD = ধ্রুবক
[∵ চতুর্ভুজের চারটি কোণের সমষ্টি 360°]
∴ ∠ABD + ∠ACD = ধ্রুবক
[∵∠BDC + ∠BAC = ধ্রুবক ]
19. O কেন্দ্রীয় একটি বৃত্তের PQ একটি জ্যা এবং AB ব্যাস।প্রমাণ কর যে AB-এর যে কোন অবস্থানে A এবং B থেকে PQ-এর উপর অঙ্কিত লম্বের সমষ্টি সর্বদা ধ্রুবক।
A এবং B বিন্দু থেকে PQ-এর উপর লম্ব যথাক্রমে AR এবং BS। O থেকে PQ-এর উপর OT লম্ব অঙ্কন করা হলো। যেহেতু, AR, BS, OT রেখাগুলি PQ সরলরেখার উপর লম্ব।
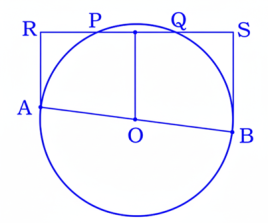
∴ AR ∥ BS ∥ OT.
∴ ABSR একটি ট্রাপিজিয়াম এবং AB ও RS-এর মধ্যবিন্দু যথাক্রমে O ও T
∴ OT = 12(AR + BS)
অর্থাৎ, AR + BS = 2OT
এখন যেহেতু O বিন্দু নির্দিষ্ট (যেহেতু এটি বৃত্তের কেন্দ্র) এবং PQ জ্যা নির্দিষ্ট অতএব, OT-এর দৈর্ঘ্য ধ্রুবক।
∴ AB-এর যে কোনো অবস্থানের জন্য (AR + BS) একটি ধ্রুবক। (প্রমাণিত)
20. ABC যে কোন একটি ত্রিভুজ। BQ এবং CP যথাক্রমে AC এবং AB-এর উপরে লম্ব। ABC ত্রিভুজের পরিবৃত্তে A বিন্দুতে AT একটি স্পর্শক। প্রমাণ কর যে, PQ ∥ AT
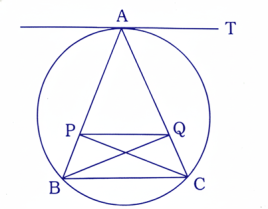
প্রমাণঃ PBCQ একটি বৃত্তস্থ চতুর্ভুজ। [∵∠BQC = ∠BPC = 90°]
∴ বহিঃস্থ ∠AQP = বিপরীত অন্তঃস্থ ∠PBC অর্থাৎ ∠ABC …… (i)
আবার, A বিন্দুতে AT বৃত্তের একটি স্পর্শক এবং A স্পর্শবিন্দু AC বৃত্তের একটি জ্যা।
∴ ∠TAC = ∠ABC …… (ii)
[AT স্পর্শকের সঙ্গে AC জ্যা দ্বারা নির্মিত কোণ বিপরীত বৃত্তাংশে অবস্থিত কোণের সমান]
∴ (i) এবং (ii) থেকে,
∠TAC = ∠AQP
কিন্তু যেহেতু এরা একান্তর কোণ ∴ PQ ∥ AT (প্রমাণিত)
21. ΔABC বৃত্তে অন্তর্লিখিত একটি সমবাহু ত্রিভুজ। BC বৃত্তচাপের উপর P একটি বিন্দু। প্রমাণ কর যে PA = PB + PC
অঙ্কনঃ AP থেকে PC-এর সমান করে AX কেটে নেওয়া হল। BX যুক্ত করা হল।
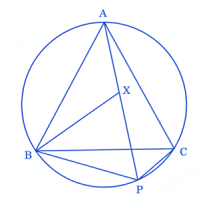 প্রমাণঃ ABX এবং BPC ত্রিভুজে
প্রমাণঃ ABX এবং BPC ত্রিভুজে
AB = BC [∵ ΔABC একটি সমবাহু ত্রিভুজ]AX = PC (অঙ্কন অনুযায়ী)
∠BAX = ∠BCP (একই বৃত্তেচাপ BP এর উপরে পরিধিস্থ কোণ)
∴ ΔABX ≅ ΔBPC (বাহু, কোণ, বাহু)
∴ BX = BP
∴ ∆BPX একটি সমদ্বিবাহু ত্রিভুজ।
∴ ∠BXP = ∠BPX
কিন্তু ∠BPX = ∠BCA = 60°, একই বৃত্তচাপ AB-এর উপরে পরিধিস্ত কোণ।
∴ ∆BPX একটি সমবাহু ত্রিভুজ [∵ সমদ্বিবাহু ত্রিভুজের একটি কোণ 60°]
∴ BX = BP = XP
∴ PA = PX + XA = BP + PC (প্রমাণিত)
22. প্রমাণ কর যে কোনো বৃত্তস্থ চতুর্ভুজের কর্ণদ্বয়ের গুণফল বিপরীত বাহুগুলির গুণফলের সমষ্টির সমান।
কল্পনাঃ ABCD একটি বৃত্তস্থ চতুর্ভুজ।
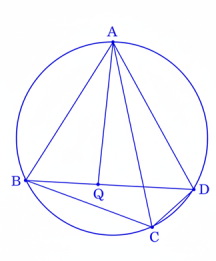 প্রমাণ করতে হবেঃ AC.BD = AB.DC = AD.BC
প্রমাণ করতে হবেঃ AC.BD = AB.DC = AD.BC
অঙ্কনঃ BD-এর উপরে Q এমন একটি বিন্দু নেওয়া হল, যাতে ∠DAQ = ∠CAB হয়।
প্রমাণঃ DAQ এবং CAB ত্রিভুজের মধ্যে,
∠DAQ = ∠CAB (অঙ্কন অনুযায়ী)
∠ADQ = ∠ACB (একই চাপের উপর কোণ)
∴ অবশিষ্ট কোণগুলিও সমান, অর্থাৎ ∠AQD = ∠ABC
∴ ত্রিভুজদ্বয় সদৃশকোণী
∴ADAC = QDBC
∴ AC.QD = AD.BC …… (i)
আবার, BAQ এবং CAD ত্রিভুজে,
∠BAQ = ∠CAD
[∵ ∠DAQ = ∠CAB ∴ ∠DAQ – ∠CAQ = ∠CAB – ∠CAQ]
∠ABQ = ∠ACD [একই চাপের উপর কোণ]
∴ ত্রিভুজদ্বয় সদৃশকোণী।
∴ ABAC = BQDC
AC.BQ = AB.DC …… (ii)
(i) এবং (ii) যোগ করে,
AC.BQ + AC.QD = AB.DC + AD.BC
বা, AC(BQ + QD) = AB.DC + AD.BC
বা, AC.BD = AB.DC + AD.BC (প্রমাণিত)
23 P কেন্দ্রবিশিষ্ট বৃত্তের একটি ব্যাস AB এবং C পরিধিস্থ যে কোনো একটি বিন্দু। C বিন্দুতে বৃত্তটির স্পর্শক, A এবং B বিন্দুতে অঙ্কিত স্পর্শক দুটিকে যথাক্রমে Q এবং R বিন্দুতে ছেদ করে। প্রমাণ কর যে, ∠QPR = 90°
অঙ্কনঃ PC যুক্ত করা হল।
প্রমাণঃ বহিস্থ বিন্দু Q থেকে QA এবং QC দুটি স্পর্শক।
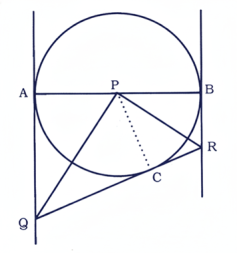 ∴ ∠APQ = ∠CPQ
∴ ∠APQ = ∠CPQ
অর্থাৎ ∴ ∠CPQ = 12 ∠APC
অনুরূপভাবে, ∠CPR =12 BPC [∵ বহিস্থ বিন্দু R থেকে RB এবং RC যথাক্রমে B এবং C বিন্দুতে বৃত্তটির দুটি স্পর্শক]
∴ ∠QPR = ∠CPQ + ∠CPR
= 12 ∠APC + 12 ∠BPC
= 12 (∠APC + ∠BPC)
= 12 ∠APB
= 12 x 180°
= 90° (প্রমাণিত)
Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
24. P এবং Q কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে বহিস্থঃভাবে A বিন্দুতে স্পর্শ করে। RS বৃত্তদুটির সরল সাধারণ স্পর্শক R এবং S যথাক্রমে বৃত্তদুটির পরিধিস্থ বিন্দু। প্রমাণ কর যে
(i) A বিন্দুতে অঙ্কিত তির্যক স্পর্শক RS-কে সমদ্বিখণ্ডিত করে।
(ii) ∠PTQ = 90° (iii) ∠RAS = 90°
প্রমাণঃ ধরা যাক, A বিন্দুতে অঙ্কিত স্পর্শক RS-কে T বিন্দুতে ছেদ করে। এখন, বহিস্থ বিন্দু T থেকে Q কেন্দ্রীয় বৃত্তে TA এবং TS দুটি স্পর্শক।
∴ TA = TS এবং TQ রেখা ∠ATS-কে সমদ্বিখণ্ডিত করে।
আবার, বহিস্থ বিন্দু T থেকে P কেন্দ্রীয় বৃত্তের TA এবং TR দুটি স্পর্শক।
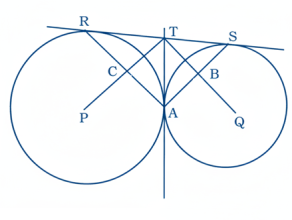 ∴ TA = TR এবং TP রেখা ∠ATR-কে সমদ্বিখণ্ডিত করে।
∴ TA = TR এবং TP রেখা ∠ATR-কে সমদ্বিখণ্ডিত করে।
সুতরাং বলা যায়, TS = TR
অর্থাৎ T হল RS-এর মধ্যবিন্দু।…… (i)
আবার, ∠PTQ = ∠PTA + ∠QTA
= 12∠ATR + 12∠ATS
= 12 (∠ATR + ∠ATS)
= 12 (∠RTS)
= 12 x 180° = 90° …… (ii)
আবার, ATR ত্রিভুজে, TA = TR, অতএব ∠TRA = ∠TAR
এবং ATS ত্রিভুজে TA = TS, অতএব ∠TSA = ∠TAS
∴ যোগ করে,
∠TRA + ∠TSA = ∠TAR + ∠TAS = ∠RAS
অর্থাৎ RAS ত্রিভুজে
∠RAS = ∠SRA + ∠RSA = 90° [∵ ত্রিভুজের একটি কোণ অপর দুই কোণের যোগফলের সমান।
25. প্রমাণ কর যে, বহিঃস্থভাবে স্পর্শ করে এমন দুটি বৃত্তের সরল সাধারণ স্পর্শকের দৈর্ঘ্যের বর্গ বৃত্তদুটির ব্যাসার্ধের গুণফলের চার গুণ।
কল্পনাঃ r1এবং r2 ব্যাসার্ধবিশিষ্ট দুটি বৃত্ত পরস্পরকে বহিঃস্থভাবে A বিন্দুতে স্পর্শ করে এবং PQ তাদের সরল সাধারণ স্পর্শক।
অঙ্কনঃ A বিন্দুতে একটি সাধারণ স্পর্শক অঙ্কন করা হল, যা PQ-কে B বিন্দুতে ছেদ করে। AR, AS, BR, BS যুক্ত করা হল।
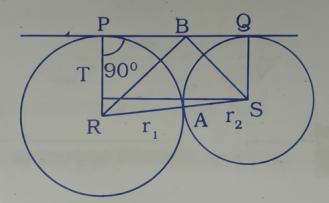 প্রমাণ করতে হবেঃ PQ2= 4r1r2
প্রমাণ করতে হবেঃ PQ2= 4r1r2
প্রথম পদ্ধতি:
PQ-এর সমান্তরাল ST অঙ্কন করা হলো।
∴ TR = PR – PT =r1 – r2
∴ RST ত্রিভুজে, পিথাগোরাসের উপপাদ্য অনুযায়ী,
TR2 + TS2 = RS2
(r1−r2)2 + PQ2 = (r1+r2)2
∴ PQ2 = (r1+r2)2 − (r1−r2)2
= 4r1r2 (প্রমাণিত)
দ্বিতীয় পদ্ধতি:
R কেন্দ্রীয় বৃত্তের দুটি স্পর্শক BP এবং BA
∴ BP = BA এবং PBA – কে BR সমদ্বিখণ্ডিত করে।
আবার S কেন্দ্রীয় বৃত্তের দুটি স্পর্শক BQ এবং BA.
∴ BQ = BA এবং ∠QBA-কে BS সমদ্বিখণ্ডিত করে।
∴∠RBS = ∠RBA + ∠ABS
=12∠PBA + 12∠QBA
=∠PBQ
= 12 x 180° = 90°
এখন, R, A, S সমরেখ এবং AB⟂RS
RBS সমকোণী ত্রিভুজে, সমকোণ B থেকে অতিভুজ RS-এর উপর BA লম্ব।
∴ ABR এবং ABS ত্রিভুজদ্বয় সদৃশকোণী।
∴ ABAS = ARAB
বা, AB2 = AR.AS = r1.r2
বা, 4AB2 = 4 r1.r2
বা, (2AB)2 = 4 r1.r2
বা, PQ2= 4 r1.r2 [∵ PQ = PB + BQ = AB + AB = 2AB] (প্রমাণিত)
26. O কেন্দ্রবিশিষ্ট একটি বৃত্তের দুটি জ্যা AC এবং BD পরস্পরকে P বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, ∠APB = 12(∠AOB +∠COD)
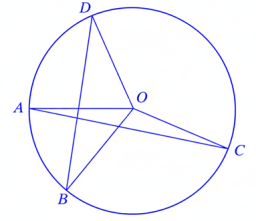
অঙ্কন:BC যুক্ত করা হল।
প্রমাণ: ∠ACB = 12∠AOB [∵ একই বৃত্তচাপ AB-এর উপরে অবস্থিত ∠AOB কেন্দ্রস্থ কোণ এবং ∠ACBপরিধিস্থ কোণ]
আবার, ∠CBD = ½ ∠COD [∵ একই বৃত্তচাপ CD-এর উপরে অবস্থিত ∠COD কেন্দ্রস্থ কোণ এবং ∠CBD পরিধিস্থ কোণ]
∴ যোগ করে
½ ∠AOB + ½ ∠COD
=∠ACB + ∠CBD
=∠PCB + ∠CBD
=∠ABP [∵ PBC ত্রিভুজ বহিঃস্থ কোণ অন্তঃস্থ বিপরীত কোণদ্বয়ের সমস্থির সমান ] (প্রমাণিত)
Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
27. কোনো বৃত্তের পরিলিখিত চতুর্ভুজের যে কোনো দুটি বিপরীত বাহুর সমষ্টি অপর দুটি বিপরীত বাহুর সমষ্টির সমান।
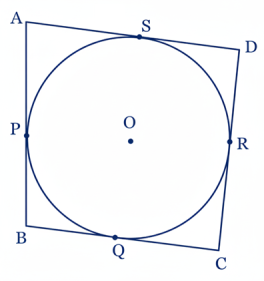 কল্পনাঃ O কেন্দ্রীয় বৃত্তের ABCD একটি পরিলিখিত চতুর্ভুজ।
কল্পনাঃ O কেন্দ্রীয় বৃত্তের ABCD একটি পরিলিখিত চতুর্ভুজ।
প্রমাণ করতে হবেঃ AB + DC = AD + BC
অঙ্কনঃ ABCD চতুর্ভুজের বাহুগুলি AB, BC, CD এবং DA বৃত্তটিকে যথাক্রমে P, Q, R এবং S বিন্দুতে স্পর্শ করে অর্থাৎ চতুর্ভুজের বাহুগুলি O কেন্দ্রীয় বৃত্তের স্পর্শক।
প্রমাণঃ এখন, যেহেতু বৃত্তের বহিঃস্থ বিন্দু থেকে অঙ্কিত স্পর্শকদ্বয়ের দৈর্ঘ্য সমান।
∴ AP = AS, BP = BQ, CQ = CR, DR = DS
∴ AB + DC = (AP + BP) + (DR + CR)
= (AS + BQ) + (DS + CQ)
= (AS + DS) + (BQ + CQ)
= AD + BC (প্রমাণিত)
28. CD সরলরেখা একটি বৃত্তকে A এবং B বিন্দুতে এমনভাবে ছেদ করে যে, AC = BD হয়। C এবং D বিন্দু দিয়ে বৃত্তটির দুটি স্পর্শক অঙ্কন করলে বৃত্তটিকে E এবং F বিন্দুতে স্পর্শ করে। প্রমাণ কর যে, AB জ্যাকে EF সমদ্বিখণ্ডিত করে।
 অঙ্কনঃ DF এবং EC –কে বর্ধিত করা হল, যারা O বিন্দুতে ছেদ করে এবং CG ∥ EFঅঙ্কন করা হল।
অঙ্কনঃ DF এবং EC –কে বর্ধিত করা হল, যারা O বিন্দুতে ছেদ করে এবং CG ∥ EFঅঙ্কন করা হল।
প্রমাণঃ OE = EF
∴ OC = OG
∴ OE-OC = OF -OG
CE = GF
এখন, CE2 = CA.CB
DF2 = DB.DA = CA.BD
∴ CE = DF
∴ GF = DF CH = HD
বা, CA + AH = HB + BD
∴ AH = HB (প্রমাণিত)
29. কোনো বৃত্তের দুটি ব্যাস AB ও CD পরস্পরের উপর লম্ব। AC বৃত্তচাপের উপর P একটি যে কোনো বিন্দু। প্রমাণ কর যে PB2 – PA2 = 4 PCD
অঙ্কনঃ PX এবং PY যথাক্রমে AB এবং DC-এর উপরে লম্ব।
PB এবং PA যথাক্রমে PBX এবং PAX ত্রিভুজের অতিভুজ। অতএব, পিথাগোরাসের উপপাদ্য অনুযায়ী,
PB2 = PX2 + BX2
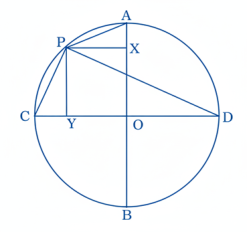 এবং PA2 = PX2 + AX2
এবং PA2 = PX2 + AX2
∴ PB2 − PA2
=(PX2 + BX2) – (PX2 + AX2)
= BX2 − AX2
= (BO + OX)2 – (AO − OX)2
= (BO2 + OX 2+ 2BO.OX) – (AO2 + OX2 -2AO.OX)
= 2 BO.OX + 2 AO.OX
=2.OX.(BO+AO)
=2.OX.AB
=2.PY.CD
=4 . 12 . PY.CD
=4△PCD
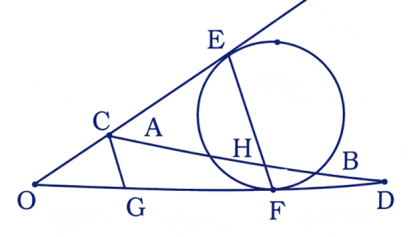
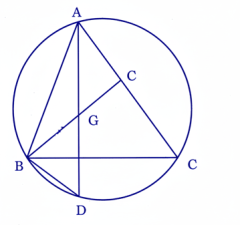 30 ABC ত্রিভুজের শীর্ষবিন্দু G। AC-কে বর্ধিত করা হলো যা BC-কে O বিন্দুতে ছেদ করে। ত্রিভুজটির বহিঃবৃত্তকে D বিন্দুতে ছেদ করে। প্রমাণ কর যে, GO = DO
30 ABC ত্রিভুজের শীর্ষবিন্দু G। AC-কে বর্ধিত করা হলো যা BC-কে O বিন্দুতে ছেদ করে। ত্রিভুজটির বহিঃবৃত্তকে D বিন্দুতে ছেদ করে। প্রমাণ কর যে, GO = DO
অঙ্কনঃ BG যুক্ত করা হলো এবং এই রেখাকে বর্ধিত করলে AC-কে X বিন্দুতে ছেদ করল। BD যুক্ত করা হলো।
প্রমাণঃ BCX এবং ACO ত্রিভুজের মধ্যে,
∠ACO = ∠BCX (সাধারণ কোণ)
∠AOC = ∠BXC (=90°) [∵ শীর্ষবিন্দু থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বের ছেদবিন্দু লম্ববিন্দু]
∴ অবশিষ্ট ∠OAC = অবশিষ্ট ∠CBX অর্থাৎ ∠CAD = ∠OBG
আবার, ∠CAD = ∠CBD [∵একই চাপ দ্বারা পরিধিস্থ কোণ]
31 ABC ত্রিভুজের ∠A-এর সমদ্বিখন্ডক BC-কে D বিন্দুতে ছেদ করে এবং ত্রিভুজটির বহিঃবৃত্তকে E বিন্দুতে ছেদ করে। প্রমাণ কর যে, AB.AC = AD.AE
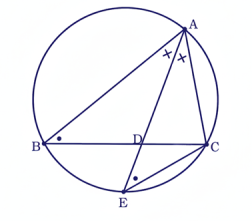 অঙ্কনঃ CE যুক্ত করা হলো।
অঙ্কনঃ CE যুক্ত করা হলো।
প্রমাণঃ ABD এবং ACE ত্রিভুজদ্বয়ে,
∠BAD = ∠CAE [কল্পনা অনুসারে ∠BAC-এর সমদ্বিখন্ডক AE]
∠ABD = ∠AEC [একই চাপের উপর কোণ]
∴ অবশিষ্ট ∠ADB = অবশিষ্ট ∠ACE
অর্থাৎ ত্রিভুজ দুটি সদৃশকোণী
∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ ADAC = ABAE
∴ বজ্রগুণন করে,
AB.AC = AD.AE (প্রমাণিত)
32 ABCD একটি বৃত্তস্থ চতুর্ভুজ। BD কর্ণ AC কর্ণকে সমদ্বিখন্ডিত করে। দেখাও যে, AB.AD = CB.CD
কল্পনা: AC এবং BD কর্ণদ্বয়ের ছেদবিন্দু P, AP = CP
প্রমাণ: APD এবং BPC ত্রিভুজদ্বয়ে,
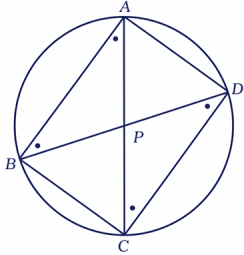 ∠APD = ∠BPC [∵বিপ্রতীপ কোণ]
∠APD = ∠BPC [∵বিপ্রতীপ কোণ]
∠ADP = ∠PCB [∵ ∠ADB এবং ∠ACB একই চাপের উপর কোণ]
∴ অবশিষ্ট ∠PAD = ∠PBC
∴ ত্রিভুজদ্বয় সদৃশকোণী
∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ ADBC = APBP …… (i)
অনুরূপভাবে, ABCD = BPCP …… (ii)
(i) এবং (ii) গুণ করে,
ADBC. ABCD = APBP . BPCP = APCP = 1 [∵ AP = CP, কল্পনা অনুসারে]
∴ AB.AD = CB.CD (প্রমাণিত)
33 যে ট্রাপিজিয়ামের সমান্তরাল বাহুগুলির অনুপাত 1 : 2, প্রমাণ কর যে তার কর্ণগুলি পরস্পরকে এক-তৃতীয়াংশে বিভক্ত করে।
ABCD ট্রাপিজিয়ামে, AD || BC, AD = 12 BC.
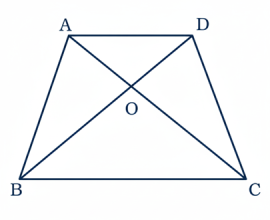 AC এবং BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে।
AC এবং BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে: AO = 13 AC
প্রমাণ: AOD এবং BOC ত্রিভুজদ্বয়ে,
∠ADO = একান্তর ∠OBC (∵ AD || BC)
∠AOD = বিপ্রতীপ ∠BOC
∴ অবশিষ্ট ∠DAO = অবশিষ্ট ∠OCB
∴ ত্রিভুজদ্বয় সদৃশকোণী
∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ AOOC = ADBC = 12 (কল্পনা অনুসারে)
∴ 2AO = OC
∴ 3AO = AO + OC = AC
∴ AO = 13 AC (প্রমাণিত)
Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
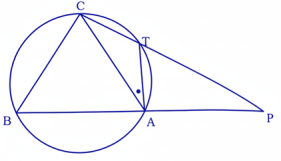
34 একটি বৃত্তের দুটি সমান জ্যা CA এবং CB। BA-কে যেকোনো বিন্দু P পর্যন্ত বর্ধিত করা হল। CP যুক্ত করা হলে, বৃত্তের T বিন্দুতে ছেদ করে। প্রমাণ কর যে, (i) ∠CAT = ∠TPA (ii) CA.CB = CP.CT
প্রমাণ: ∠CBA + ∠CTA = 180° [ ∵ ABCT একটি বৃত্তস্থ চতুর্ভুজ]
∴ ∠CAB + ∠CTA = 180° [ ∵ CB = CA ∴∠CBA = ∠CAB]
আবার, ∠CAB + ∠CAP= 180° [ ∵ BAP একটি সরলরেখা]
 ∴ ∠CAB + ∠CTA = ∠CAB + ∠CAP
∴ ∠CAB + ∠CTA = ∠CAB + ∠CAP
∴ ∠CTA = ∠CAP
এখন, CTA এবং CPA ত্রিভুজদ্বয়ে,
∠CTA = ∠CAP (আগেই প্রমাণিত)
∠ACT = ∠ACP (সাধারণ কোণ)
অবশিষ্ট ∠CAT = অবশিষ্ট ∠CPA
∴ ∠CAT = ∠TPA
এখন যেহেতু CTA এবং CPA ত্রিভুজদ্বয় সদৃশকোণী,
অতএব তাদের অনুরূপ বাহুগুলিও সমানুপাতী
∴ CTCA = CACP বা CTCB = CACP [ ∵ CA = CB ]
∴ CA.CB = CP.CT] (প্রমাণিত)
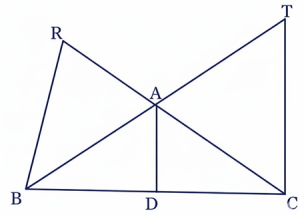
35 ABC যেকোনো একটি ত্রিভুজের BC বাহুর উপর D যেকোনো একটি বিন্দু। AD যুক্ত করা হল। B এবং C বিন্দুতে AD-এর সমান্তরাল BR এবং CT অঙ্কন করা হল, BA এবং CA-কে বর্ধিত করা হল, যা সমান্তরাল বাহুদ্বয়কে যথাক্রমে T এবং R বিন্দুতে ছেদ করে। প্রমাণ কর যে, 1AD = 1RB + 1TC
প্রমাণ: BAD এবং BTC ত্রিভুজদ্বয়ে, ∠ABD = ∠TBC (সাধারণ কোণ) ∠ADB = ∠TCB (∵ AD || TC)
∴ অবশিষ্ট কোণদ্বয় সমান অর্থাৎ, ত্রিভুজদ্বয় সদৃশকোণী
 ∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ ADTC = BDBC …… (i)
অনুরূপভাবে, RBC এবং ADC ত্রিভুজদ্বয় সদৃশকোণী,
অতএব অনুরূপ বাহুগুলি সমানুপাতী
∴ ADRB = DCBC …… (ii)
(i) এবং (ii) যোগ করে,
ADTC + ADRB = BDBC + DCBC
AD (1TC + 1RB) = BDBC + DCBC = BD+CDBC = BCBC = 1
∴ 1AD = 1RB + 1TC (প্রমাণিত)
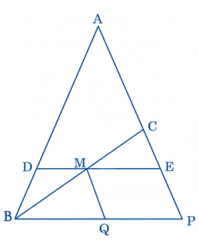
36 ABC ত্রিভুজের ভূমি BC-এর মধ্যবিন্দু M দিয়ে DME একটি সরলরেখা এমনভাবে অঙ্কন করা হল, যাতে তা AB এবং বর্ধিত AC থেকে দুটি সমান অংশ AD এবং AE কেটে নেয়। প্রমাণ কর যে, BD = CE
অঙ্কনঃ B বিন্দু দিয়ে DME-এর সমান্তরাল BP অঙ্কন করা হল, যা বর্ধিত AE-কে P বিন্দুতে ছেদ করে এবং AP-এর সমান্তরাল MQ অঙ্কন করা হল।
প্রমাণঃ এখন ABP ত্রিভুজে, যেহেতু DE || BP এবং AD = AE∴ DB = EP …… (i)
BPC ত্রিভুজে, MQ || CP
 ∴ MQCP = BMBC বা, MQCP = BM2BM = 12
∴ MQCP = BMBC বা, MQCP = BM2BM = 12
∴ CP = 2MQ
বা, CE + EP = 2EP [∵ MQ = EP, MQPE সামান্তরিক হওয়ায়]
বা, CE = EP …… (ii)
(i) এবং (ii) থেকে
BD = CE (প্রমাণিত)
37 ABCD একটি ট্রাপিজিয়াম এর AC এবং BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করে। তির্যক বাহুদ্বয় DA এবং CB কে বর্ধিত করলে P বিন্দুতে ছেদ করে। প্রমাণ কর যে, AB-কে PO সমদ্বিখন্ডিত করে।
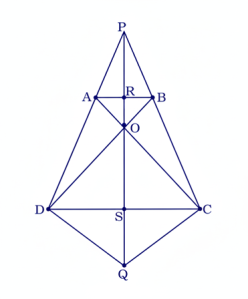 অঙ্কনঃ D বিন্দু দিয়ে AC-এর সমান্তরাল সরলরেখা অঙ্কন করা হল, এবং PO-কে বর্ধিত করা হল, যারা Q বিন্দুতে ছেদ
অঙ্কনঃ D বিন্দু দিয়ে AC-এর সমান্তরাল সরলরেখা অঙ্কন করা হল, এবং PO-কে বর্ধিত করা হল, যারা Q বিন্দুতে ছেদ
করল। QC যুক্ত করা হল। PQ, AB-কে R বিন্দুতে ছেদ করে।
প্রমাণঃএখন PDQ ত্রিভুজে, AC || DQ অর্থাৎ OC || DQ
∴ PAAD = POOQ
এবং PDC ত্রিভুজে, AB || DC
∴ PAAD = PBBC
∴ POOQ = PBBC
∴ OB || BC অর্থাৎ DO || QC
∴ OCQD একটি সামান্তরিক
∴ DC এবং OQ কর্ণদ্বয় পরস্পরকে S বিন্দুতে সমদ্বিখন্ডিত করে অর্থাৎ, DC-এর মধ্যবিন্দু।
অর্থাৎ, DS = SC অর্থাৎ, DS = 12DC অর্থাৎ, DSDC = 12
এখন, PDS ত্রিভুজে, PAPD = ARDS
এবং PDC ত্রিভুজে, PAPD = ABDC
∴ ARDS = ABDC অর্থাৎ, ARAB = DSDC = 12
∴ AB-এর মধ্যবিন্দু R।
38 ABCD এবং AECF দুটি সামান্তরিক এবং EF ও AD পরস্পর সমান্তরাল। যদি AF ও DE ছেদ করে G বিন্দুতে এবং BF ও CE ছেদ করে H বিন্দুতে, তবে প্রমাণ কর যে, GH || AB.
প্রমাণ: DGA এবং EGF ত্রিভুজদ্বয়ে,
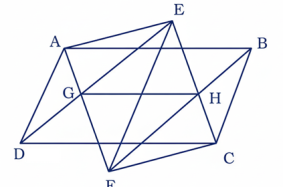 ∠ADG = একান্তর ∠PEF (∵ AD || EF)
∠ADG = একান্তর ∠PEF (∵ AD || EF)
∠GAD = একান্তর ∠GFE (∵ AD || EF)
∠DGA = বিপ্রতীপ ∠EGF
∴ ত্রিভুজদ্বয় সদৃশকোণী
∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ FGGA =EFAD…… (i)
অনুরূপভাবে, EHF এবং BCH ত্রিভুজদ্বয় সদৃশকোণী
অর্থাৎ, FHHB =EFBC…… (ii)
(i) এবং (ii) থেকে
FGGA =EFAD=EFBC =FHHB [ ∵ AD = BC]
∴FAB ত্রিভুজে, FGGA = FHHB ∴ GH || AB (প্রমাণিত)
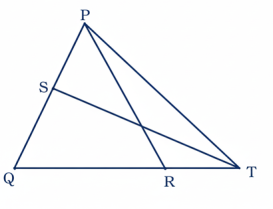
39 PQR ত্রিভুজে PQ = PR। PQ-এর মধ্যবিন্দু S এবং PQ–এর লম্ব সমদ্বিখন্ডক ভূমি QR-এর বর্ধিতাংশকে T বিন্দুতে ছেদ করে। প্রমাণ কর যে, PQ² = QR.QT.
অঙ্কন: PT যুক্ত করা হল।
প্রমাণ: এখন PTS এবং QTS ত্রিভুজদ্বয়ে,
PS = SQ (∵ PQ-এর মধ্যবিন্দু S)
 ST সাধারণ বাহু
ST সাধারণ বাহু
∠PST = ∠QST (=90°)
∴ ত্রিভুজদ্বয় সর্বসম
∴ ∠TPS = ∠TQS অর্থাৎ ∠TPQ = ∠RQP
আবার, PQR এবং PQT ত্রিভুজদ্বয়ে,
∠PQT = ∠PRQ [ ∵ ∆PQR সমদ্বিবাহু]
= ∠TPQ [ (i) থেকে]
∠Q সাধারণ
∴ অবশিষ্ট ∠PTQ = ∠QPR
∴ ত্রিভুজদ্বয় সদৃশকোণী অতএব অনুরূপ
∴ QRPQ = PQQT
∴ PQ² = QR.QT (প্রমাণিত)
40 ABCD একটি রম্বস। C বিন্দু দিয়ে অঙ্কিত সরলরেখা AD-কে P বিন্দুতে এবং বর্ধিত AB-কে Q বিন্দুতে ছেদ করে। যদি DP = 12 AB হয়, দেখাও যে, BQ = 2AB.
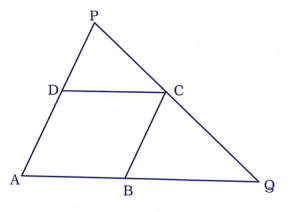 প্রমাণ: ধরা যাক, AB = BC = CD = DA = x, ∴ DP = 12 x
প্রমাণ: ধরা যাক, AB = BC = CD = DA = x, ∴ DP = 12 x
এখন, PDC এবং CBQ ত্রিভুজদ্বয়ে,
∠PDC = ∠CQB [ ∵ DC || AQ এবং PQ ছেদক]
∠DPC = ∠BCQ [ ∵ BC || AD এবং PQ ছেদক]
∴ অবশিষ্ট কোণদ্বয় সমান
∴ ত্রিভুজদ্বয় সদৃশকোণী অতএব অনুরূপ
অর্থাৎ অনুরূপ বাহুগুলি সমানুপাতী
∴ DPBC = DCBQ
∴ 12xx = xBQ ∴ 12 = ABBQ
∴ BQ = 2AB (প্রমাণিত)
41 ABCD একটি সামান্তরিকের BC এবং CD বাহুর মধ্যবিন্দু P এবং Q। AP এবং AQ রেখাংশ কর্ণ BD-কে যথাক্রমে K এবং L বিন্দুতে ছেদ করে। প্রমাণ কর যে BK = KL = LD = 13 BD
প্রমাণ: AKD এবং BKP ত্রিভুজদ্বয়ে,
∠AKD = ∠BKP (বিপ্রতীপ কোণ)
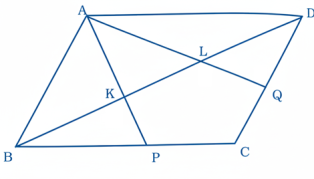 ∠ADK = একান্তর ∠KBP (∵ AD || BP)
∠ADK = একান্তর ∠KBP (∵ AD || BP)
∴ অবশিষ্ট ∠DAK = ∠KPB
∴ ত্রিভুজদ্বয় সদৃশকোণী
∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ KDBK=ADBP=(2BPBP=21)
∴ 1 + KDBK = 1 + 21 = 3
∴ BK + KDBK 31
∴ BDBK = 31 ∴ BD = 3BK ∴ BK = 13BD
অনুরূপভাবে ABL এবং LDQ ত্রিভুজদ্বয় অনুরূপ, অতএব, LD = 13BD
∴ BK = KL = LD = 13 BD (প্রমাণিত)
42 একটি সমকোণী ত্রিভুজের বাহুগুলি ক্রমিক সমানুপাতী হলে এবং তার সমকোণ থেকে অতিভুজের উপর লম্ব অঙ্কন করা হলে, দেখাও যে অতিভুজের বৃহত্তম অংশটি ত্রিভুজের ক্ষুদ্রতম বাহুর সমান।
কল্পনা: ABC ত্রিভুজের ∠BAC = 90° এবং AD ⊥ BC, (CD > BD)
প্রমাণ করতে হবে যে, CD = AB
AB ক্ষুদ্রতম বাহু। AB, AC, BC ক্রমিক সমানুপাতিক।
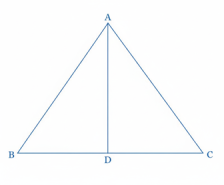 অর্থাৎ, AB : AC = AC : BC অর্থাৎ, AC² = AB.BC. ……(i)
অর্থাৎ, AB : AC = AC : BC অর্থাৎ, AC² = AB.BC. ……(i)
প্রমাণ: ACD এবং ABC ত্রিভুজদ্বয়ে, ∠ADC = ∠BAC = 90°
∠C সাধারণ
∴ অবশিষ্ট ∠DAC = ∠ABC
∴ ত্রিভুজদ্বয় সদৃশকোণী
∴ অনুরূপ বাহুগুলি সমানুপাতী
CDAC = ACBC ∴ AC² = CD. BC ……(ii)
(i) এবং (ii) তুলনা করে,
AB.BC = CD.BC
∴ AB = CD (প্রমাণিত)
43 ABCD একটি সামান্তরিক, AD-এর সামান্তরাল সরলরেখার উপর E এবং F দুটি বিন্দু। AE, DF-কে বর্ধিত করলে তা P বিন্দুতে এবং BE, CF-কে বর্ধিত করলে তা Q বিন্দুতে ছেদ করে। প্রমাণ কর যে, PQ || AB.
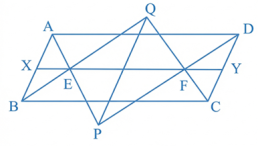 প্রমাণ : APD এবং EPF ত্রিভুজদ্বয়ে,
প্রমাণ : APD এবং EPF ত্রিভুজদ্বয়ে,
∠PDA = ∠PFE (∵ EF || AD)
∠P সাধারণ কোণ
এবং অবশিষ্ট ∠PAD = ∠PEF
∴ ত্রিভুজদ্বয় সদৃশকোণী
∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ PAPE = PDPF = ADEF
অনুরূপভাবে, QBC এবং QEF সদৃশকোণী
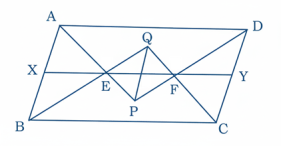 ∴ QBQE = QCQF = BCEF
∴ QBQE = QCQF = BCEF
কিন্তু, ADEF = BCEF (∵ AD = BC)
∴ PAPE= QBQE বা, PAPE − 1 = QBQE − 1 বাAEPE= BEQE
এখন, AEB এবং PEQ ত্রিভুজদ্বয়ে,
∠AEB = বিপ্রতীপ ∠PEQ এবং AE:PE = BE:QE
∴ ত্রিভুজদ্বয় অনুরূপ
∴ ∠EAB = ∠EPQ
কিন্তু এরা একান্তর কোণ
∴ PQ || AB (প্রমাণিত)
Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications
44 ABC সমকোণী ত্রিভুজের ∠A সমকোণ, BC অতিভুজের উপর AD লম্ব প্রমাণ কর যে, ΔABCΔACD = BC2AC2
প্রমাণ : ∆ABC = 12 BC.AD∆ADC = 12 DC.AD
∴ ΔABCΔACD = 12BC.AD12DC.AD
এখন, যেহেতু ∆ADC এবং ∆BAC সদৃশকোণী
অনুরূপ বাহুগুলি সমানুপাতী
∴DC AC = AC BC
বা DC= AC BC . AC
বা, 1DC= BCAC2
∴ ΔABCΔACD =BCDC =BC.1DC=BC.BCAC2= BC2AC2 (প্রমাণিত)
45 প্রমাণ কর যে, কোন ত্রিভুজের শীর্ষবিন্দু থেকে লম্ববিন্দুর দৈর্ঘ্য শীর্ষবিন্দুর বিপরীত বাহু থেকে পরিকেন্দ্রের দৈর্ঘ্যের দ্বিগুণ।
কল্পনা
ABC ত্রিভুজে, বাহু BC এবং CA-এর উপরে যথাক্রমে AX এবং BY উচ্চতা, তারা পরস্পর O বিন্দুতে ছেদ করে,
অর্থাত্ O লম্ববিন্দু।
আবার, BC এবং CA বাহুদ্বয়ের লম্ব সমদ্বিখন্ডক PR এবং QR,
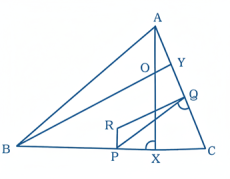 তারা পরস্পর R বিন্দুতে ছেদ করে, অর্থাৎ R পরিকেন্দ্র।
তারা পরস্পর R বিন্দুতে ছেদ করে, অর্থাৎ R পরিকেন্দ্র।
প্রমাণ করতে হবে যে,
AO = 2PR বা BO = 2RQ
অঙ্কন
P ও Q যুক্ত করা হল।
প্রমাণ
এখন, RQ || BY (∵ তারা একই সরলরেখা AC-এর উপর লম্ব)
এবং RP || AX, (∵ তারা একই সরলরেখা BC-এর উপর লম্ব)
আবার, PQ || AB এবং PQ = 12 AB (∵ ABC ত্রিভুজের BC এর CA বাহুর মধ্যবিন্দু P এবং Q)
∴ ∆ABO-এর তিনটি বাহু AO, BO, AB ত্রিভুজ PQR-এর যথাক্রমে PR, PQ এবং PQ-এর সঙ্গে সমান্তরাল।
∴ ABO এবং PQR ত্রিভুজদ্বয় সদৃশকোণী।
অনুরূপ বাহুগুলি সমানুপাতী
∴ AQ PR= BO RQ = AQ PQ = 2 1
কিন্তু AB = 2PQ
∴ AO = 2PR এবং BO = 2RQ (প্রমাণিত)
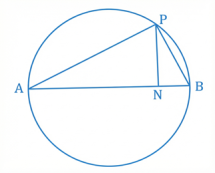
46 APB বৃত্তের P বিন্দু থেকে অঙ্কিত লম্ব ব্যাস AB কে N বিন্দুতে ছেদ করে। প্রমাণ কর যে, PB² = AB.NB.
প্রমাণ: AB ব্যাস
∴ ∠APB = 90° (∵ অর্ধবৃত্তস্থ কোণ)
এখন, PAB এবং PNB ত্রিভুজদ্বয়ে,
∠APB = ∠PNB (= 90°)
 ∠B সাধারণ কোণ
∠B সাধারণ কোণ
∴ অবশিষ্ট ∠PAB = ∠NPB
∴ ত্রিভুজদ্বয় সদৃশকোণী
∴ অনুরূপ বাহুগুলি সমানুপাতী
∴ AB:PB = PB:NB
∴ PB² = AB. NB. (প্রমাণিত)
47 একটি বৃত্তের ব্যাস AB, AP এবং AQ জ্যা দুটির বর্ধিত করলে B বিন্দুতে অঙ্কিত স্পর্শককে তারা যথাক্রমে X এবং Y বিন্দুতে ছেদ করে, দেখাও যে,
(i) APQ এবং AXY ত্রিভুজদ্বয় অনুরূপ (ii) P, Q, Y, X বিন্দু চারটি সমবৃত্তস্থ
অঙ্কন: PQ এবং BQ যুক্ত করা হল
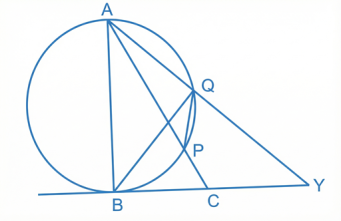 প্রমাণ: ∠AQB = 90° (∵∠A অর্ধবৃত্তস্থ কোণ)
প্রমাণ: ∠AQB = 90° (∵∠A অর্ধবৃত্তস্থ কোণ)
∠ABY = 90° (∵ AB ব্যাস স্পর্শক BY এর ছেদবিন্দুতে লম্ব)
এবং ∠APQ = ∠ABQ (∵একই চাপের উপরস্থ কোণ)
= 90° – ∠BAQ [ ∵ ∆ABQ-এ, ∠ABQ + ∠BAQ + 90°]
= ∠AYB [∵ ∆ABY-এ, ∠BAO + ∠AYB = 90°]
এখন APQ এবং AXY ত্রিভুজদ্বয়
∠APQ = ∠AYX (আগেই প্রমাণিত)
∠A সাধারণ কোণ
∴অবশিষ্ট ∠AQP = ∠AXY (প্রমাণিত)
∴ত্রিভুজদ্বয় সদৃশকোণী অতএব আনুরূপ (প্রমাণিত)
আবার, ∠QPX + ∠QYX = ∠QPX + ∠APQ [∵∠AYB = ∠APQ আগেই প্রমাণিত]
= 2 সমকোণ
∵ PQYX একটি বৃত্তস্থ চতুর্ভুজ।
অর্থাৎ P, Q, Y, X বিন্দুগুলি সমবৃত্তস্থ (প্রমাণিত)
Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications Upapadyera prayoga o samadhan|Application and solution of the theorem|উপপাদ্যের প্রয়োগ ও সমাধান|Geometry theorem applications



