
Trigonometry

Assertion Reason Questions-
Assertion: The value of each of the trigonometric ratios of an angle does not depend on the size of the triangle. It only depends on the angle.
Reason: In right ![]() as hypotenuse is the longest side.
as hypotenuse is the longest side.
Assertion: Sin 60o = Cos 30o
Reason: Sin 2θ = Sin θ where θ is an acute angle.
Answer Key-
Multiple Choice questions-
Very Short Answer :
∵ sec θ is in the denominator
∴ The min. value of sec θ will return max. value for 1secθ.
But the min. value of sec θ is sec 0° = 1.
Hence, the max. value of 1secθ∘ = 11 = 1
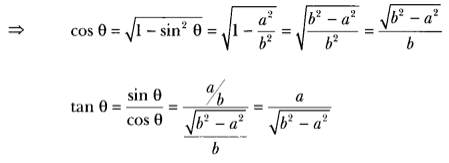
It means value of θ = 45°
Now, 2 tan θ + cos2 θ = 2 tan 45° + cos2 45°
⇒ cos [90° – (x – 20)°] = cos (3x – 10)°
By comparing the coefficient
90° – x° + 20° = 3x° – 10° = 110° + 10° = 3x° + x°
120° = 4x°
⇒120∘4 = 30°
⇒ sin2A = 12 (1)2 [∵ tan 45° = 1]
= sin2 A = 12
⇒ sin A = 1√2
Hence, ∠A = 45°
b2x2 + a2y2 – a2b2 = b2(acos θ)2 + a2(b sin θ)2 – a2b2
= a2b2 cos2θ + a2b2 sin2 θ – a2b2 = a2b2 (sin2 θ + cos2 θ) – a2b2
= a2b2 – a2b2 = θ (∵ sin2 θ + cos2 θ = 1)
tan A = cot B
⇒ tan A = tan (90° – B)
A = 90° – B
[∵ Both A and B are acute angles]
⇒ A + B = 90°
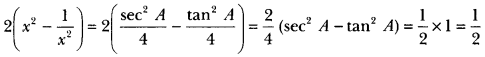
∴ ∠A + ∠B = 180° – ∠C = 90°
Now, sin2 A + sin2 B = sin2 A + sin2 (90° – A) = sin2 A + cos2 A = 1
sec 4 A = cosec (A – 20°)
⇒ cosec (90° – 4 A) = cosec (A – 20°)
∴ 90° – 4 A = A – 20°
⇒ 90° + 20° = A + 4 A
⇒ 110° = 5 A
∴ A = 1105 = 22°
Short Answer :
Now, we know that
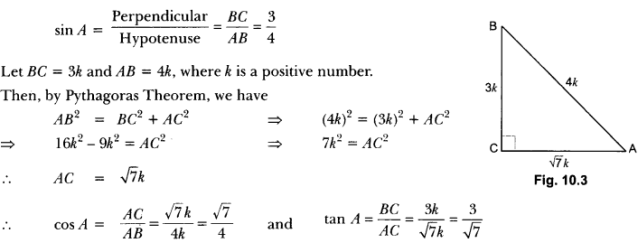
Now, we have, 15 cot A = 8

PR2 = PO2 + QR2
⇒ (13)2 = (12)2 + QR2
⇒ 169 = 144 + QR2
⇒ QR2 = 169 – 144 = 25
⇒ QR = 5 cm
Now, tan P = QRPQ =512 and cot R =QRPQ =512
tan P – cot R = 512 – 512 = 0
⇒ (sin θ + cos θ)2 = 3
⇒ sin2 θ + cos2 θ + 2 sin θ cos θ = 3
⇒ 2 sin cos θ = 2 (∵ sin2 θ + cos2 θ = 1)
⇒ sin θ. cos θ = 1 = sin2 θ + cos2 θ
![]()
⇒ 1 = tan θ + cot θ = 1
Therefore tan θ + cot θ = 1

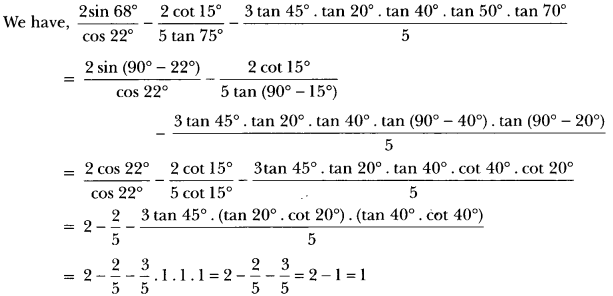
= sin (90° – 65°). cos 65° + cos (90° – 65°). sin 65°
= cos 65° . cos 65° + sin 65°. sin 65°
= cos2 65° + sin2 65° = 1.
3 cos 68°. cosec 22° – 12 tan 43°. tan 47°. tan 12°. tan 60°. tan 78°.
= 3 cos (90° – 22°). cosec 22° – 12 . {tan 43° . tan (90° – 43°)}. {tan 12°. tan (90° – 12°). tan 60°}
= 3 sin 22°. cosec 22° – 12 (tan 43° . cot 43°). (tan 12°. cot 12°). tan 60°
= 3 × 1 – × 1 × 1 × √3 = 3 –3√2 = 6−√3√2.
Long Answer :
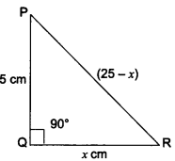
We have a right-angled ∆PQR in which ∠Q = 90°.
Let QR = x cm
Therefore, PR = (25 – x) cm
By Pythagoras Theorem, we have
PR2 = PQ2 + QR2
(25 – x)2 = 52 + x2
= (25 – x)2 – x2 = 25
(25 – x – x) (25 – x + x) = 25
(25 – 2x) 25 = 25
25 – 2x = 1
25 – 1 = 2x
= 24 = 2x
∴ x = 12 cm
Hence, QR = 12 cm
PR = (25 – x) cm = 25 – 12 = 13 cm
PQ = 5 cm
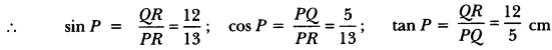

We have a right-angled ∆ABC in which ∠B = 90°.
and, tan A =1√3
Now, tan A = 1√3 = BCAB
Let BC = k and AB = √3k
∴ By Pythagoras Theorem, we have
⇒ AC2 = AB2 + BC2
⇒ AC2 = (√3k)2 + (k)2 = 3k2 + k2
⇒ AC2 = 4k2


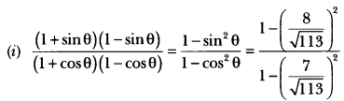
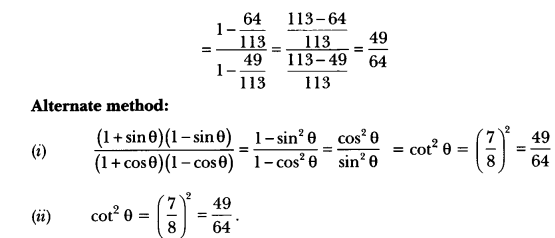
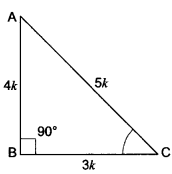
Let us consider a right triangle ABC in which ∠B = 90°
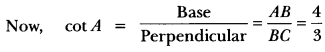
Let AB = 4k and BC = 3k
∴ By Pythagoras Theorem
AC2 = AB2 + BC2
AC = (4k)2 + (3k)2 = 16k2 + 9k2
AC2 = 25k2
∴ AC = 5k


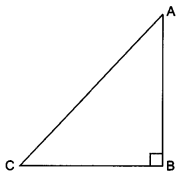
Let us consider a right-angled ∆ABC in which ∠B = 90°.
For ∠A we have
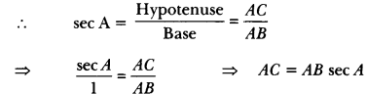
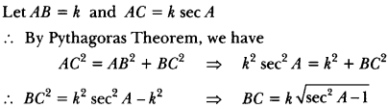
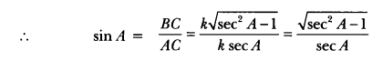
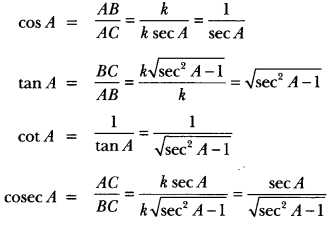
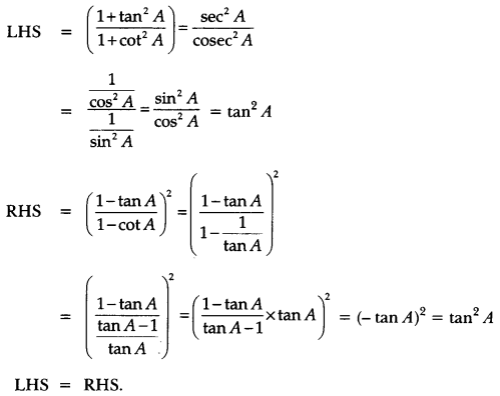
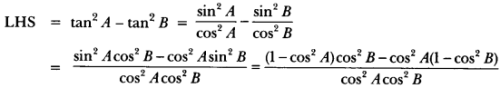
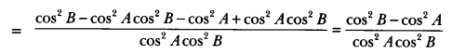
![]()
![]()
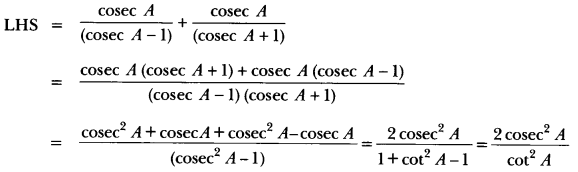
= 2 cosec2 A tan2 A = 2(1 + cot2 A). tan2 A
= 2 tan2 A + 2 tan2 A. cot2 A (∵ tan A cot A = 1)
= 2 + 2 tan2 A = 2(1 + tan2 A) = 2 sec2 A = RHS.
LHS = (sin θ + sec θ)2 + (cos θ + cosec θ)2
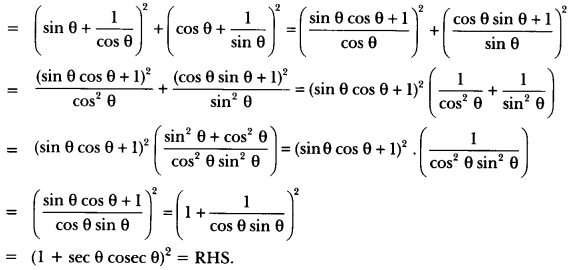
= (1 + sec θ cosec θ)2 = RHS.
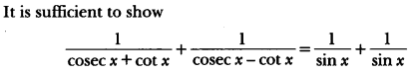
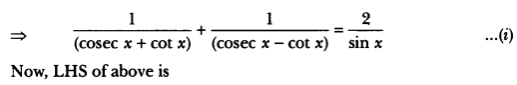

Case Study Answers:

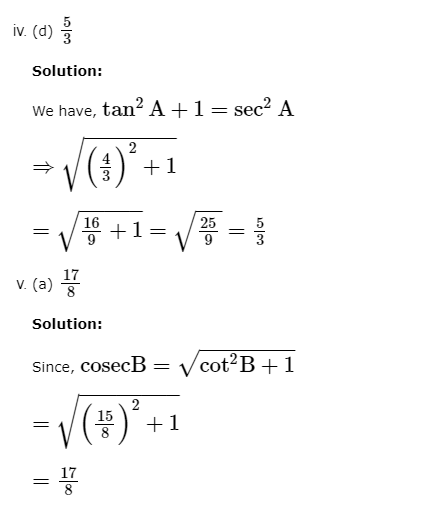
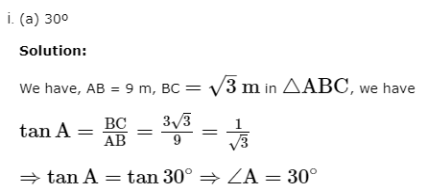
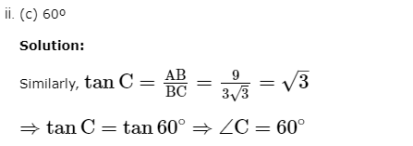
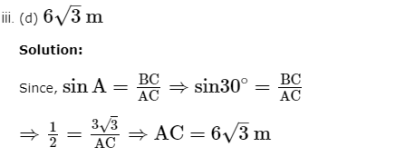
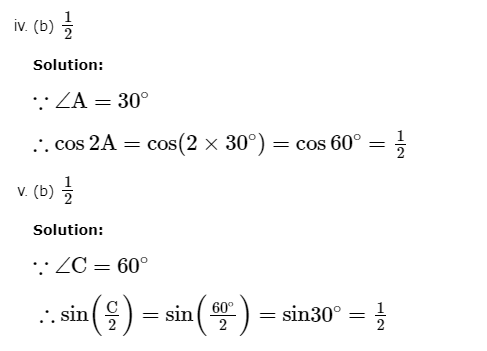
Assertion Reason Answer-





