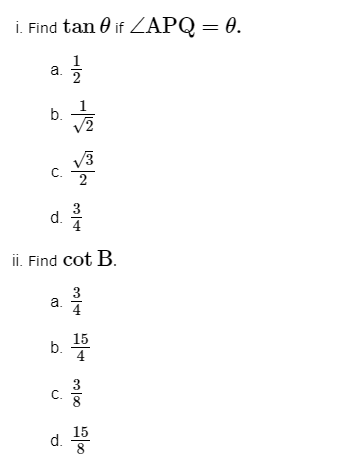Important Questions
Multiple Choice questions-
1. If cos (α + β) = 0, then sin (α – β) can be reduced to
(a) cos β
(b) cos 2β
(c) sin α
(d) sin 2α
2. If cos (40° + A) = sin 30°, the value of A is:?
(a) 60°
(b) 20°
(c) 40°
(d) 30°
3. If sin x + cosec x = 2, then sin 19 x + cosec 20 x =
(a) 2 19
(b) 2 20
(c) 2
(d) 2 39
4. If cos 9a = sin a and 9a < 90°, then the value of tan 5a is
(a) 1 √ 3 . .
(b) √ 3
(c) 1
(d) 0
5. (1 + tanθ + secθ ) (1 + cotθ – cosecθ ) is equal to
(a) 0
(b) 1
(c) 2
(d) -1
6. Ratios of sides of a right triangle with respect to its acute angles are known as
(a) trigonometric identities
(b) trigonometry
(c) trigonometric ratios of the angles
(d) none of these
7. The value of cos θ cos( 90° – θ) – sin θ sin (90° – θ) is:
(a) 1
(b) 0
(c) -1
(d) 2
8. If x = a cos θ and y = b sin θ, then b 2 x 2 + a 2 y 2 =
(a) ab
(b) b 2 + a 2
(c) a 2 b 2
(d) a 4 b 4
9. If x and y are complementary angles, then
(a) sin x = sin y
(b) tan x = tan y
(c) cos x = cos y
(d) sec x = cosec y
10. sin (45° + θ) – cos (45° – θ) is equal to
(a) 2 cos θ
(b) 0
(c) 2 sin θ
(d) 1
Very Short Questions:
1. Find maximum value of 1 s e c θ . . , 0°≤ θ ≤ 90°.
2. Given that sin θ = a b . . , find the value of tan θ.
3. If sin θ = cos θ, then find the value of 2 tan θ + cos 2 θ.
4. If sin (x – 20)° = cos (3x – 10)°, then find the value of x.
5. If sin 2 A = 1 2 . . tan 2 45°, where A is an acute angle, then find the value of A.
6. If x = a cos θ, y = b sin θ, then find the value of b 2 x 2 + a 2 y 2 – a 2 b 2 .
7. If tan A = cot B, prove that A + B = 90°.
8. If sec A = 2x and tan A = 2x, find the value of 2(x 2 − 1 x 2 . . ) .
9. In a ∆ABC, if ∠ C = 90 ° , prove that sin 2 A + sin 2 B = 1.
10. If sec 4A = cosec (A – 20°) where 4 A is an acute angle, find the value of A.
Short Questions :
1. If sin A = 3 4 . . , calculate cos A and tan A.
2. Given 15 cot A = 8, find sin A and sec A.
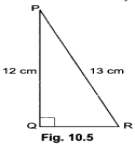
3. In Fig. 10.5, find tan P – cot R.
4. If sin θ + cos θ = √ 3 , then prove that tan θ + cot θ = 1.
5. Prove that 1 − s i n θ 1 + s i n θ . . = (sec θ – tan θ) 2
6.
7.
8.
9. Evaluate: sin 25° cos 65° + cos 25° sin 65°.
10. Without using tables, evaluate the following:
3 cos 68°. cosec 22° – 1 2 . . tan 43°. tan 47°. tan 12°. tan 60°. tan 78°
Long Questions :
1. In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
2. In triangle ABC right-angled at B, if tan A = 1 √ 3 . . find the value of:
( i ) sin A cos C + cos A sin C (ii) cos A cos C – sin A sin C.
3. If cot θ = 7 8 . . , evaluate:
( i )
(ii) cot 2 θ
4. If 3 cot A = 4, check whether 1 − tan 2 . A 1 + tan 2 . A . . = cos 2 A – sin 2 A or not.
5. Write all the other trigonometric ratios of ∠ A in terms of sec A.
6. Prove that
7. Prove that:
8. Prove that:
9. Prove that: (sin θ + sec θ) 2 + (cos θ + cosec θ) 2 = (1 + sec θ cosec θ) 2 .
10. Prove that:
Assertion Reason Questions-
1. Two aeroplanes leave an airport, one after the other. After moving on runway, one flies due North and other flies due South. The speed of two aeroplanes is 400km/ hr and 500km/ hr respectively. Considering PQ as runway and A and B are any two points in the path followed by two planes, then answer the following questions.
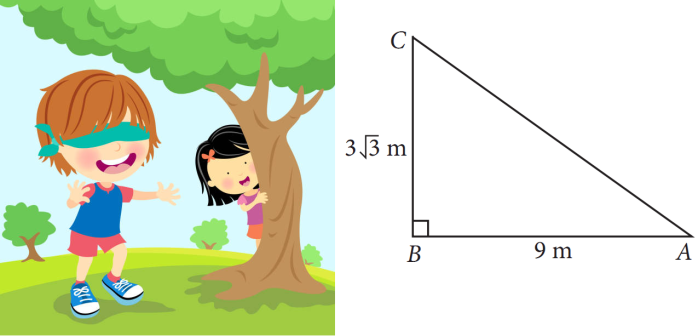
2. Three friends – Anshu, Vijay and Vishal are playing hide and seek in a park. Anshu and Vijay hide in the shrubs and Vishal have to find both of them. If the positions of three friends are at A, B and C respectively as shown in the figure and forms a right angled triangle such that AB = 9 m, BC = √ 3 M and then answer the following questions.
Post navigation

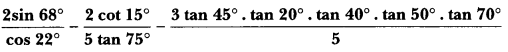
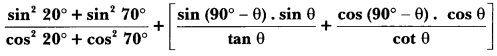
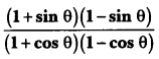
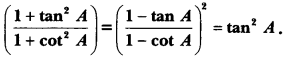
![]()
![]()