
Trigonometry
Introduction to Trigonometry
The word trigonometry is derived from the Greek words ‘tri’ meaning three, ‘gon’ meaning sides and ‘metron’ meaning measure.
Trigonometry is the study of relationships between the sides and the angles of the triangle.
Angle measured in anticlockwise direction is taken as positive angle whereas the angle measured in clockwise direction is taken as negative angle.
Ratio of the sides of a right triangle with respect to the acute angles is called the trigonometric ratios
of the angle.
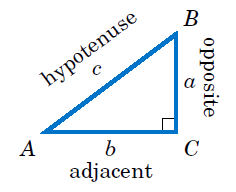
Trigonometric ratios of the acute angle A in right triangle ABC are given as follows:
It states that “in a right triangle, square of the hypotenuse is equal to the sum of the squar es of the other two sides”.
Pythagoras theorem can be used to obtain the length of the side of a right angled triangle when the other two sides are already given.
The ratios cosec A, sec A and cot A are the reciprocals of the ratios sin A, cos A and tan A respectively as given:
Two angles are said to complementary angles if their sum is equal to 90o. Based on this relation, the trigonometric ratios of complementary angles are given as follows:
Note: tan 0o = 0 = cot 90o, sec 0o = 1 = cosec 90o, sec 90o, cosec 0o, tan 90o and cot 0o are not defined.
An equation involving trigonometric ratios of an angle, say θ, is termed as a trigonometric identity if it is satisfied by all values of θ.
In the ΔABC right-angled at B, BC is the side opposite to ∠A, AC is the hypotenuse and AB is the side adjacent to ∠A.
For the right ΔABC, right-angled at ∠B, the trigonometric ratios of the ∠A are as follows:
sin A = opposite side/hypotenuse = BC/AC
cos A = adjacent side/hypotenuse = AB/AC
tan A = opposite side/adjacent side = BC/AB
cosec A = hypotenuse/opposite side = AC/BC
sec A = hypotenuse/adjacent side = AC/AB
cot A = adjacent side/opposite side = AB/BC
Draw a circle of the unit radius with the origin as the centre. Consider a line segment OP joining a point P on the circle to the centre which makes an angle θ with the x-axis. Draw a perpendicular from P to the x-axis to cut it at Q.
Sinθ = PQ/OP=PQ/1=PQ
cosθ = OQ/OP=OQ/1=OQ
tanθ = PQ/OQ=sinθ/cosθ
cosecθ = OP/PQ=1/PQ
secθ = OP/OQ=1/OQ
cotθ = OQ/PQ=cosθ/sinθ

cosec θ = 1/sin θ
sec θ = 1/cos θ
tan θ = sin θ/cos θ
cot θ = cos θ/sin θ = 1/tan θ

tanθ and secθ are not defined at 90∘.
cotθ and cosecθ are not defined at 0∘.
As θ increases from 0∘ to 90∘
sin θ increases from 0 to 1
cos θ decreases from 1 to 0
tan θ increases from 0 to ∞
cosec θ decreases from ∞ to 1
sec θ increases from 1 to ∞
cot θ decreases from ∞ to 0
In Mathematics, the complementary angles are the set of two angles such that their sum is equal to 90°. For example, 30° and 60° are complementary to each other as their sum is equal to 90°. In this article, let us discuss in detail about the complementary angles and the trigonometric ratios of complementary angles with examples in a detailed way.
If θ is an acute angle, its complementary angle is 90∘ − θ. The following relations hold true for trigonometric ratios of complementary angles.
sin (90∘ − θ) = cos θ
cos (90∘ − θ) = sin θ
tan (90∘ − θ) = cot θ
cot (90∘ − θ) = tan θ
cosec (90∘ − θ) = sec θ
sec (90∘ − θ) = cosec θ
Finding Trigonometric Ratios of Complementary Angles
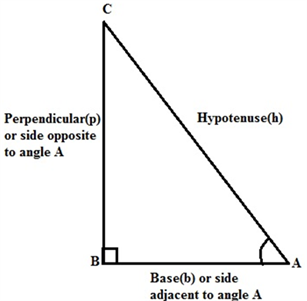
∠A and ∠C form a complementary pair.
⇒ ∠A + ∠C = 90°
The relationship between the acute angle and the lengths of sides of a right-angle triangle is expressed by trigonometric ratios. For the given right angle triangle, the trigonometric ratios of ∠A is given as follows:
sin A = BC/AC
cos A = AB/AC
tan A =BC/AB
csc A = 1/sin A = AC/BC
sec A =1/cos A = AC/AB
cot A = 1/tan A = AB/BC
The trigonometric ratio of the complement of ∠A. It means that the ∠C can be given as 90° – ∠A
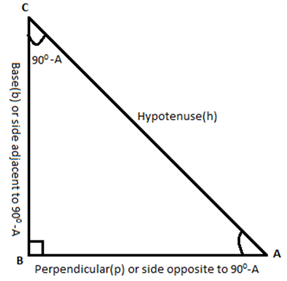
As ∠C = 90°- A (A is used for convenience instead of ∠A ), and the side opposite to 90° – A is AB and the side adjacent to the angle 90°- A is BC as shown in the figure given above.
Therefore,
sin (90°- A) = AB/AC
cos (90°- A) = BC/AC
tan (90°- A) = AB/BC
csc (90°- A) =1/sin (90°- A) = AC/AB
sec (90°- A) = 1/cos (90°- A) = AC/BC
cot (90°- A) = 1/tan (90°- A) = BC/AB
Comparing the above set of ratios with the ratios mentioned earlier, it can be seen that;
sin (90°- A) = cos A ; cos (90°- A) = sin A
tan (90°- A) = cot A; cot (90°- A) = tan A
sec (90°- A) = csc A; csc (90°- A) = sec A
These relations are valid for all the values of A that lies between 0° and 90°.
Trigonometric Identities are useful whenever trigonometric functions are involved in an expression or an equation. Trigonometric Identities are true for every value of variables occurring on both sides of an equation. Geometrically, these identities involve certain trigonometric functions (such as sine, cosine, tangent) of one or more angles.
Sine, cosine and tangent are the primary trigonometry functions whereas cotangent, secant and cosecant are the other three functions. The trigonometric identities are based on all the six trig functions. Check Trigonometry Formulas to get formulas related to trigonometry.
Trigonometric Identities are useful whenever trigonometric functions are involved in an expression or an equation. Trigonometric Identities are true for every value of variables occurring on both sides of an equation. Geometrically, these identities involve certain trigonometric functions (such as sine, cosine, tangent) of one or more angles.
Sine, cosine and tangent are the primary trigonometry functions whereas cotangent, secant and cosecant are the other three functions. The trigonometric identities are based on all the six trig functions. Check Trigonometry Formulas to get formulas related to trigonometry.

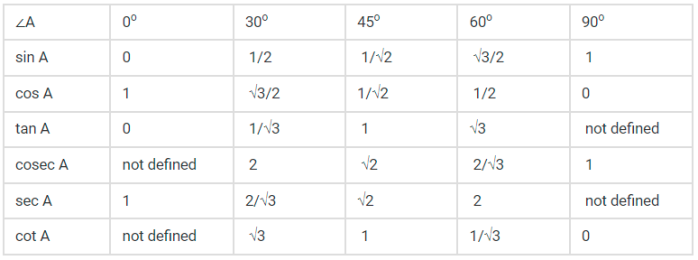
|
∠A |
0° |
30° |
45° |
60° |
90° |
|
sin A |
0 |
12 |
1√2 |
√32 |
1 |
|
cos A |
1 |
√32 |
1√2 |
12 |
0 |
|
tan A |
0 |
1√3 |
1 |
√3 |
Not defined |
|
cosec A |
Not defined |
2 |
√2 |
2√3 |
1 |
|
sec A |
1 |
2√3 |
√2 |
2 |
Not defined |
|
cot A |
Not defined |
√3 |
1 |
1√3 |
0 |






