Triangles
Answer Key-
Multiple Choice questions-
Very Short Answer :
∴ The third side is proportional to the corresponding third side.
i.e., The two triangles will be similar by SSS criterion.

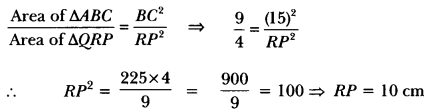
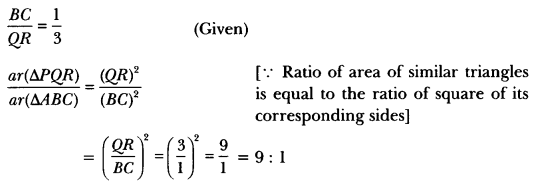

∴ The given triangle is not a right triangle.
= 180° – (55° + 25°) = 100° = ∠M
∠Q = ∠S = 25° (Given)
∆QPR ~ ∆STM
i.e., . ∆QPR is not similar to ∆TSM.
∴ ∠A = ∠D = 47°
∠B = ∠E = 63°
∴ ∠C = 180° – (∠A + ∠B) = 180° – (47° + 63°) = 70°
∴ Given statement is true.
∴ AB2 = AC2 + BC2 [By Pythagoras theorem]
⇒ AB2 = AC2 + AC2
[∵ AC = BC]
⇒ AB2 = 2AC2
Short Answer :
DE || BC,
∴ ADDB=AEEC [By Basic Proportionality Theorem]
⇒xx−2 = x+2x−1
⇒ x(x – 1) = (x – 2) (x + 2)
⇒ x2 – x = x2 – 4
⇒ x = 4
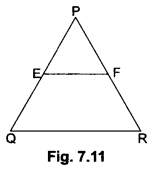
We have, PQ = 1.28 cm, PR = 2.56 cm
PE = 0.18 cm, PF = 0.36 cm
Now, EQ = PQ-PE = 1.28 – 0.18 = 1.10 cm and
FR = PR – PF = 2.56 – 0.36 = 2.20 cm
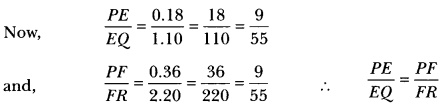
Therefore, EF || QR [By the converse of Basic Proportionality Theorem]
Now, in ∆ABC and ∆DEF, we have

h = 42 Hence, height of tower, DE = 42m
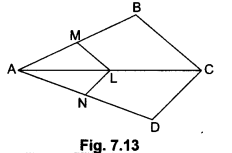
Firstly, in ∆ABC, we have
LM || CB (Given)
Therefore, by Basic Proportionality Theorem, we have


DE || OQ (Given)

[Applying the converse of Basic Proportionality Theorem in ∆PQR]
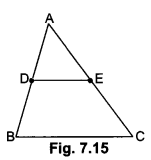
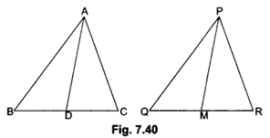
Given: ∆ABC in which D and E are the mid-points of sides AB and AC respectively.
To prove: DE || BC
Proof: Since D and E are the mid-points of AB and AC respectively
∴ AD = DB and AE = EC
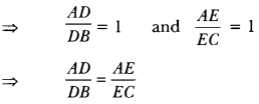
DB EC Therefore, DE || BC (By the converse of Basic Proportionality Theorem)


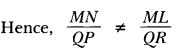
∆NML is not similar to ∆PQR.

⇒ DC = 10 cm.

In ∆ABE and ∆CFB, we have
∠AEB = ∠CBF (Alternate angles)
∠A = ∠C (Opposite angles of a parallelogram)
∴ ∆ABE ~ ∆CFB (By AA criterion of similarity)
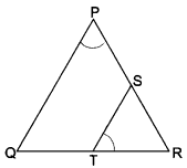
In ∆RPQ and ∆RTS, we have
∠RPQ = ∠RTS (Given)
∠PRQ = ∠TRS = ∠R (Common)
∴ ∆RPQ ~ ∆RTS (By AA criterion of similarity)
Long Answer :
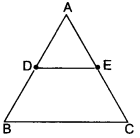
Given: A ∆ABC in which D is the mid-point of AB and DE is drawn parallel to BC, which meets AC at E.
To prove: AE = EC
Proof: In ∆ABC, DE || BC
∴ By Basic Proportionality Theorem, we have
ADDB =AANDANDC … (i)
Now, since D is the mid-point of AB
⇒ AD = BD … (ii)
From (i) and (ii), we have
ADDB = AANDANDC
⇒ 1 =AANDANDC
Hence, E is the mid-point of AC.

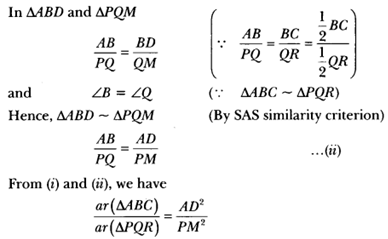
∠B = ∠Q (∵ ∆ABC ~ ∆PQR) … (i)
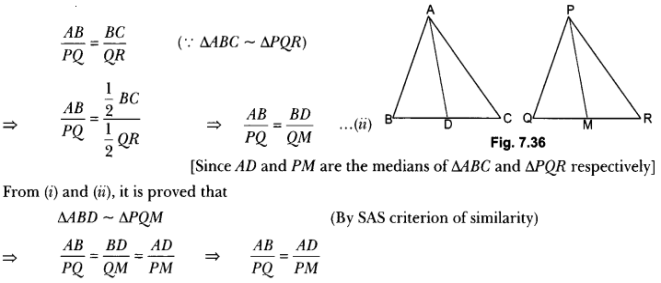
∠1 = ∠2 [Alternate angles]
∠3 = ∠4 [Alternate angles]
∠CED = ∠AEB [Vertically opposite angles]
∴ ∆EDC ~ ∆EBA [By AA criterion of similarity]
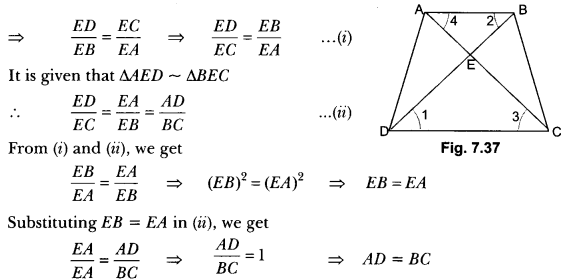
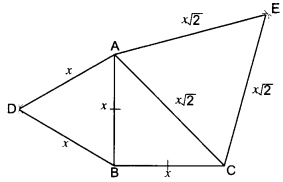
Given: A ∆ABC in which ∠ABC = 90° and AB = BC.
∆ABD and ΔCAE are equilateral triangles.
To Prove: ar(∆ABD) = 12 × ar(∆CAE)
Proof: Let AB = BC = x units.
∴ hyp. CA = √x2 + √x2 = x√2 units.
Each of the ABD and ∆CAE being equilateral has each angle equal to 60°.
∴ ∆АВD ~ ∆CAE
But, the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
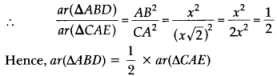
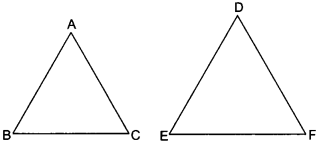
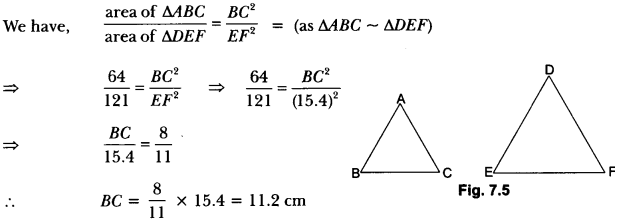
Given: Two triangles ABC and DEF, such that
∆ABC ~ ∆DEF and area (∆ABC) = area (∆DEF)
To prove: ∆ABC ≅ ∆DEF
Proof: ∆ABC ~ ∆DEF
⇒ ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
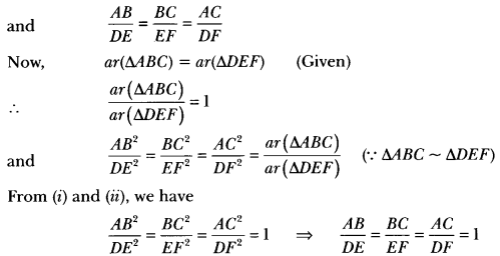
AB = DE, BC = EF, AC = DF
∆ABC ≅ ∆DEF (By SSS criterion of congruency)
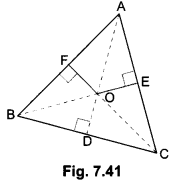
Join OA, OB and OC.
(i) In right ∆’s OFA, ODB and OEC, we have
OA2 = AF2 + OF2 … (i)
WHETHER2 = BD2 + FROM2 … (ii)
and C2 = EC2 + OE2
Adding (i), (ii) and (iii), we have
⇒ 0A2 + OB2 + OC2 = AF2 + BD2 + EC2 + OF2 + FROM2 + OE2
⇒ 0A2 + OB2 + OC2 – IP2 – OE2 – OF2 = AF2 + BD2 + EC2
(ii) We have, OA2 + OB2 + OC2 – IP2 – OE2 – OF2 = AF2 + BD2 + EC2
⇒ (OA2 – OE2) + (OB2 – OF2) – (OC2 – IP2) = AF2 + BD2 + EC2
⇒ AE2 + CD2 + BF2 = AP2 + BD2 + EC2
[Using Pythagoras Theorem in ∆AOE, ∆BOF and ∆COD]
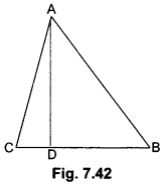
We have, DB = 3CD
Now,
BC = BD + CD
⇒ BC = 3CD + CD = 4CD (Given DB = 3CD)
∴ CD = 14 BC
and DB = 3CD = 14BC
Now, in right-angled triangle ABD using Pythagoras Theorem we have
AB2 = AD2 + DB2 … (i)
Again, in right-angled triangle ∆ADC, we have
AC2 = AD2 + CD2 … (ii)
Subtracting (ii) from (i), we have
AB2 – AM2 = DB2 – CD2
∴ 2AB2 – 2AM2 = BC2
⇒ 2AB2 = 2AM2 + BC2
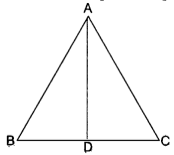
Let ABC be an equilateral triangle and let AD ⊥ BC.
∴ BD = DC
Now, in right-angled triangle ADB, we have
AB2 = AD2 + BD2 [Using Pythagoras Theorem]
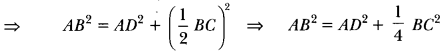
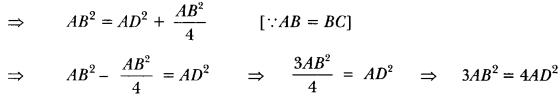
Case Study Answers:
|
i |
c |
90º |
|
ii |
b |
SAS |
|
iii |
b |
4 : 9 |
|
iv |
d |
The converse of Pythagoras theorem |
|
v |
a |
48 cm2 |
|
i |
b |
AB, AC |
|
ii |
d |
AB2 = BC2 + CA2 |
|
iii |
c |
6.5m |
|
iv |
b |
10m |
|
v |
a |
6.7m (approx) |
Assertion Reason Answer-






