Triangles

Two geometrical figures are called congruent if they superpose exactly on each other, that is, they are of the same shape and size.

Two figures are similar, if they are of the same shape but not necessarily of the same size.

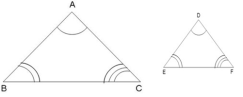
Two triangles are equiangular if their corresponding angles are equal. The ratio of any two corresponding sides in such triangles is always the same.

If a line is drawn parallel to one side of a triangle to intersect other two sides in distinct points, the other two sides are divided in the same ratio.

If a line divides any two sides of a triangle in the same ratio then the line is parallel to the third side.

If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.

If two angles of a triangle are respectively equal to two angles of another triangle, then by the angle sum property of a triangle their third angles will also be equal.

Thus, AAA similarity criterion changes to AA similarity criterion which can be stated as follows:

If two angles of one triangle are respectively equal to two angles of other triangle, then the two triangles are similar.

If two triangles are similar, then their corresponding angles are equal.

If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar.

If two triangles are similar, then their corresponding sides are in constant proportion.

If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.

If two triangles are similar, then one of the angles of one triangle is equal to the corresponding angle of the other triangle and the sides including these angles are in constant proportion.

If in two right triangles, hypotenuse and one side of one triangle are proportional to the hypotenuse and one side of another triangle, then the two triangles are similar. This criteria is referred as the RHS similarity criterion

In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Thus, in triangle ABC right angled at B, AB² + BC² = AC²

If in a triangle, square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

Thus, if Δ ABC Δ PQR, then${\frac{ar\Delta ABC}{ar\Delta PQR}=\left(\frac{AB}{PQ}\right)}^2{=\left(\frac{BC}{QR}\right)}^2{=\left(\frac{CA}{RP}\right)}^2$

Also, the ration of the areas of two similar triangles is equal to the ration of the squares of the corresponding medians.

In an equilateral or an isosceles triangle, the altitude divides the base into two equal parts.

If a perpendicular is drawn from the vertex of the right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.

The area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonal.

Sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

In an equilateral triangle, three times the square of one side is equal to four times the square of one of its altitudes.

To find whether the given two triangles are similar or not, it has four criteria. They are:

Side-Side- Side (SSS) Similarity Criterion – When the corresponding sides of any two triangles are in the same ratio, then their corresponding angles will be equal and the triangle will be considered as similar triangles.

Angle Angle Angle (AAA) Similarity Criterion – When the corresponding angles of any two triangles are equal, then their corresponding side will be in the same ratio and the triangles are considered to be similar.

Angle-Angle (AA) Similarity Criterion – When two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are considered as similar.

Side-Angle-Side (SAS) Similarity Criterion – When one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportional), then the triangles are said to be similar.

Statement: As per Pythagoras theorem, “In a right-angled triangle, the sum of squares of two sides of a right triangle is equal to the square of the hypotenuse of the triangle.”

Proof –

Consider the right triangle, right-angled at B.

Construction-

Draw BD ⊥ AC

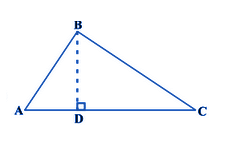
Now, △ADB ~ △ABC

So, AD/AB = AB/AC

or AD. AC = AB² ……………(i)

Also, △BDC ~ △ ABC

So, CD/BC = BC/AC

or, CD. AC = BC² ……………(ii)

Adding (i) and (ii),

AD. AC + CD. AC = AB² + BC²

AC (AD + DC) = AB² + BC²

AC (AC) = AB² + BC²

⇒ AC² = AB² + BC²

Hence, proved.

A girl having a height of 90 cm is walking away from a lamp-post’s base at a speed of 1.2 m/s. Calculate the length of that girl’s shadow after 4 seconds if the lamp is 3.6 m above the ground.

S and T are points on sides PR and QR of triangle PQR such that angle P = angle RTS. Now, prove that triangle RPQ and triangle RTS are similar.

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD

at F. Show that triangles ABE and CFB are similar.

Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90°. The sides of a right triangle (say a, b and c) which have positive integer values, when squared, are put into an equation, also called a Pythagorean triple.

History

The theorem is named after a greek Mathematician called Pythagoras.

Pythagoras Theorem Formula

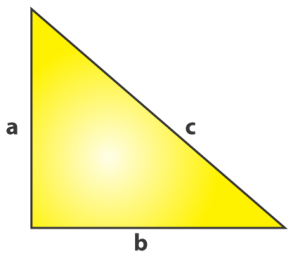
Consider the triangle given above:

Where “a” is the perpendicular,

“b” is the base,

“c” is the hypotenuse.

According to the definition, the Pythagoras Theorem formula is given as:

Hypotenuse² = Perpendicular² + Base²

c² = a² + b²

The side opposite to the right angle (90°) is the longest side (known as Hypotenuse) because the side opposite to the greatest angle is the longest.

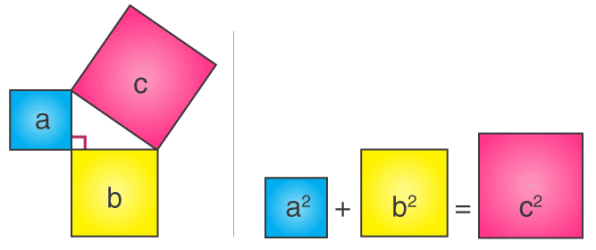
Consider three squares of sides a, b, c mounted on the three sides of a triangle having the same sides as shown.

By Pythagoras Theorem –

Area of square “a” + Area of square “b” = Area of square “c”

Pythagoras Theorem Proof

Given: A right-angled triangle ABC, right-angled at B.

To Prove- AC² = AB² + BC²

Construction: Draw a perpendicular BD meeting AC at D.

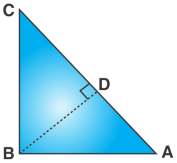
Proof:

We know, △ADB ~ △ABC

Therefore,

$\begin{array}{c}\frac{AD}{AB}=\frac{AB}{AC}\end{array}$

(corresponding sides of similar triangles)

Or, AB² = AD × AC ……………………………..……..(1)

Also, △BDC ~△ABC

Therefore,

$\begin{array}{c}\frac{CD}{BC}=\frac{BC}{AC}\end{array}$

(corresponding sides of similar triangles)

Or, BC²= CD × AC ……………………………………..(2)

Adding the equations (1) and (2) we get,

AB² + BC² = AD × AC + CD × AC

AB² + BC² = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC² = AB² + BC²

Hence, the Pythagorean theorem is proved.