
Surface Areas and Volumes
Surface Areas and Volumes
Total surface area = 2(ℓb + bh + hℓ) Volume = ℓ × b × h
Diagonal of a cuboid =
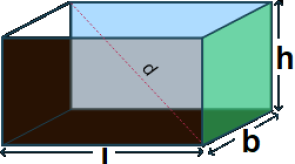
Surface Area and Volume of Cuboid
A cuboid is the region covered by its six rectangular faces. The surface area of a cuboid is equal to the sum of the areas of its six rectangular faces.
Surface area of the cuboid
Consider a cuboid whose dimensions are l × b × h, respectively.
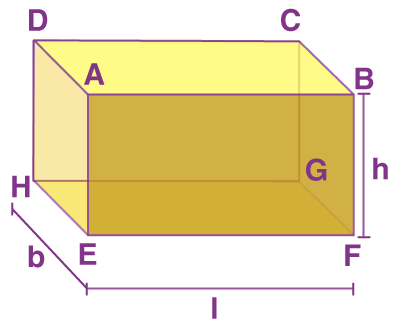
Cuboid with length l, breadth b and height h
The total surface area of the cuboid (TSA) = Sum of the areas of all its six faces
TSA (cuboid) = 2(l × b) + 2(b × h) + 2(l × h) = 2(lb + bh + lh)
Lateral surface area (LSA) is the area of all the sides apart from the top and bottom faces.
The lateral surface area of the cuboid = Area of face AEHD + Area of face BFGC + Area of face ABFE + Area of face DHGC
LSA (cuboid) = 2(b × h) + 2(l × h) = 2h(l + b)
Length of diagonal of a cuboid =√(l2 + b2 + h2)
Lateral surface area = 4 × (edge)2
Total surface area = 6 × (edge)2
Volume = (edge)3
Diagonal of a cube =√3×edge
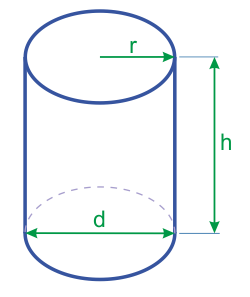
Surface Area and Volume of Cylinder
A cylinder is a solid shape that has two circular bases, connected with each other, through a lateral surface. Thus, there are three faces, two circular and one lateral, of a cylinder. Based on these dimensions, we can find the surface area and volume of a cylinder.
Surface Area of Cylinder
Take a cylinder of base radius r and height h units. The curved surface of this cylinder, if opened along the diameter (d = 2r) of the circular base can be transformed into a rectangle of length 2πr and height h units. Thus,

Transformation of a Cylinder into a rectangle.
CSA of a cylinder of base radius r and height h = 2π × r × h
TSA of a cylinder of base radius r and height h = 2π × r × h + area of two circular bases
=2π × r × h + 2πr2
=2πr (h + r)
Volume of a Cylinder
Volume of a cylinder = Base area × height = (πr2) × h = πr2h
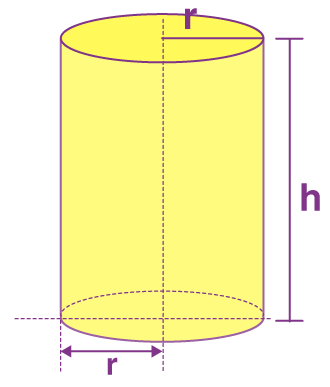
Cylinder with height h and base radius r
Area of curved surface or lateral surface area = perimeter of the base x height =2πrh
Total surface area (including both ends) =2πrh+πr2+2πr (h+r)
Volume = Area of the base × height = πr2h
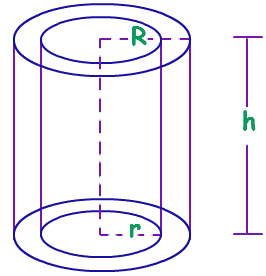
Area of each end =πR2−πr2
Area of curved surface =2π (R+r)h
Total surface area = (Area of curved surface) + 2(Area of each end)
=2π (R+r)h+(πR2−πr2)
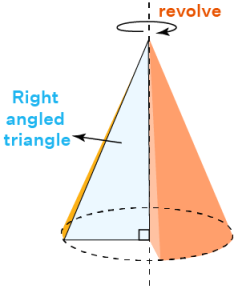
Slant height (ℓ) =√h2+r2
Area of curved surface =πrl= πr√h2+r2
Total surface area = Area of curved surface + Area of base =πrl+πr2=πr(l+r)
Volume =13πr2h
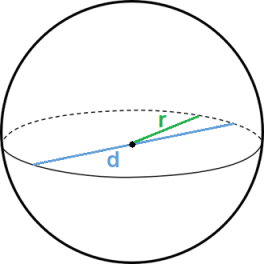
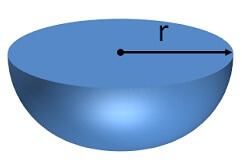
Surface area =πr2
Volume =43πr3
Area of curved surface =2πr2
Total surface Area = Area of curved surface + Area of base
=2πr2+πr2=3πr2
Volume =23πr3
Surface Area of Combined Figures
Areas of complex figures can be broken down and analysed as simpler known shapes. By finding the areas of these known shapes, we can find out the required area of the unknown figure.
Example: 2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Length of each cube = 64(1/3) = 4cm
Since these cubes are joined adjacently, they form a cuboid whose length l = 8 cm. But height and breadth will remain the same = 4 cm.
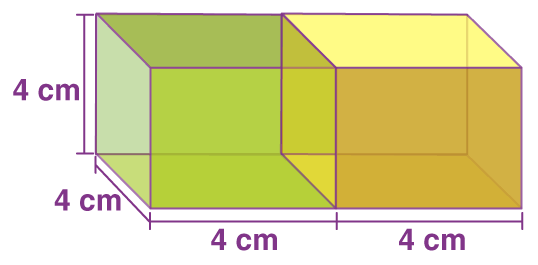
Combination of 2 equal cubes
∴ The new surface area, TSA = 2(lb + bh + lh)
TSA = 2 (8 x 4 + 4 x 4 + 8 x 4)
= 2(32 + 16 + 32)
= 2 (80)
TSA = 160 cm2
Volume of Combined Solids
The volume of complex objects can be simplified by visualising them as a combination of shapes of known solids.
Example: A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 3 cm and the height of the cone is equal to 5 cm.
This can be visualised as follows:
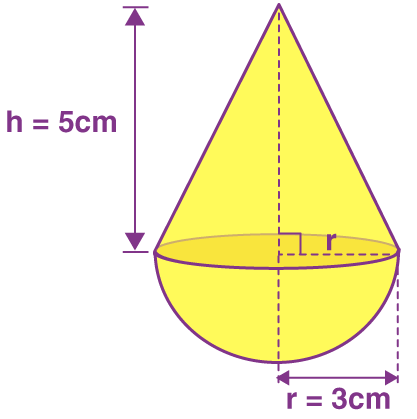
Volume of combined solids
V(solid) = V(Cone) + V(hemisphere)
V(solid) = (1/3)πr2h + (2/3)πr3
V(solid) = (1/3)π(9)(5) + (2/3)π(27)
V(solid) = 33π cm3
Surface area and volume of Frustum of a cone
When a solid is cut by a plane, then another form of solids is formed. One such form of solid is the frustum of a cone, which is formed when a plane cuts a cone parallelly to the base of the cone. Let us discuss its surface area and volume here.
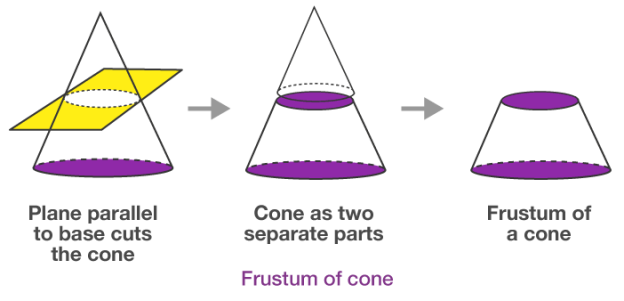
If a right circular cone is sliced by a plane parallel to its base, then the part with the two circular bases is called a Frustum.
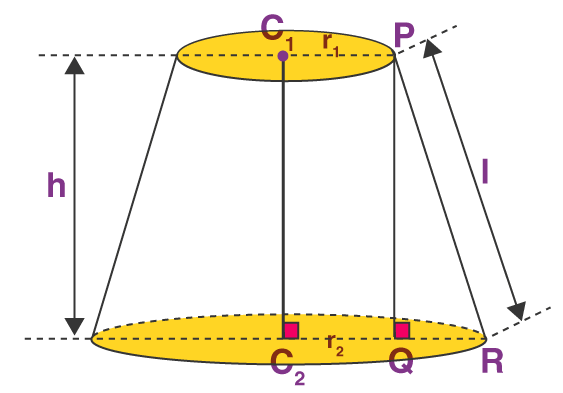
Frustum with radius r1 and r2 and height h
CSA of frustum = π(r1 + r2)l, where l = √[h2 + (r2 – r1)2]
TSA of the frustum is the CSA + the areas of the two circular faces = π(r1 + r2)l + π(r12 + r22)
Volume of a Frustum
The volume of a frustum of a cone =(1/3)πh(r12 + r22 + r1r2)
Important Questions
Multiple Choice questions-
1. If the surface areas of two spheres are in ratio 16 : 9, then their volumes will be in the ratio:
(a) 27 : 64
(b) 64 : 27
(c) 4 : 3
(d) 3 : 4
2. A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes?
(a) 3 : 1 : 2
(b) 3 : 2 : 1
(c) 1 : 2 : 3
(d) 1 : 3 : 2
3. If the area of three adjacent faces of cuboid are X, Y and Z respectively, then the volume of cuboid is:
(a) XYZ
(b) 3XYZ
(c) √xyz
(d) √3xyz
4. The volumes of two spheres are in the ratio 27 : 8. The ratio of their curved surface is:
(a) 9 : 4
(b) 4 : 9
(c) 3 : 2
(d) 2 : 3
5. The ratio of the volumes of two spheres is 8 : 27. If r and R are the radii of spheres respectively, then (R – r): r is:
(a) 1 : 2
(b) 1 : 3
(c) 2 : 3
(d) 4 : 9
6. The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is:
(a) 27 : 20
(b) 20 : 27
(c) 9 : 4
(d) 4 : 9
7. If the radius of base of a right circular cylinder is halved, keeping the height same, the ratio of the volume of the reduced cylinder to that of the original cylinder is:
(a) 2 : 3
(b) 3 : 4
(c) 1 : 4
(d) 4 : 1
8. If the volumes of a cube is 1728 cm³, the length of its edge is equal to:
(a) 7 cm
(b) 12 cm
(c) 18 cm
(d) 19 cm
9. The volume (in cm³) of the largest right circular cone that can be cut off from a cube of edge 4.2 cm is: .
(a) 9.7
(b) 72.6
(c) 58.2
(d) 19.4
10. The circumference of the edge of hemispherical bowl is 132 cm. When π is taken as 227, the capacity of bowl in cm³ is:
(a) 2772
(b) 924
(c) 19404
(d) 9702
Very Short Questions:
Short Questions :
OR
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Long Questions :
Case Study Questions:
190.93cm3
75cm3
77cm3
83.5cm3
4.75cm3
8.18cm3
2.76cm3
75cm3
17.5cm2
7.9cm2
19.64cm2
15.5cm2
175.50cm3
182.75cm3
76.85cm3
96cm3

Assertion Reason Questions-
Assertion: If diameter of a sphere is decreased by 25%, then its curved surface area is decreased by 43.75%.
Reason: Curved surface area is increased when diameter decreases
Assertion: The external dimensions of a wooden box are 18 cm, 10 cm and 6 cm respectively and thickness of the wood is 15 mm, then the internal volume is 765 cm3.
Reason: If external dimensions of a rectangular box be l, b and h and the thickness of its sides be x , then its internal volume is (l – 2x) (b – 2x) (h – 2x).
Answer Key-
Multiple Choice questions-
Very Short Answer :
Capacity of the given vessel
= capacity of cylinder – capacity of hemisphere
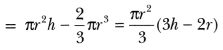
= curved surface area of cone + curved surface area of cylinder + area of the base.
![]()
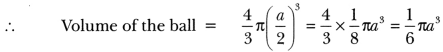
Breadth (b) = 5 cm, Height (h) = 5 cm
Surface Area = 2 (lb + bh + lh)
= 2(10 × 5 + 5 × 5 + 5 × 10) = 2 × 125 = 250 cm2
= 49 × 33 × 24 = 43 πr2
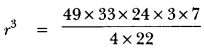
r = 21 cm
= 78 × 270 × 300 × 350
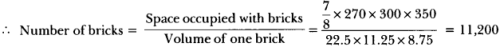
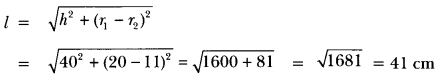
Volume of hemisphere = Surface area of hemisphere
= 23πr2 = 3πr2 = , units r = 92 units.
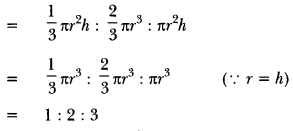
Short Answer :
Then, diameter of the sphere that will fit inside the given cube = a
∴ Volume of the cube : Volume of the sphere.
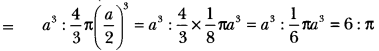
Then, R – r = 4, l = 5
We know, l2 = (R – r)2 + h2
⇒ 52 = 42 + h2 or h2 = 25 – 16 = 9
⇒ h = 3 cm
Then, 2πr = 18 and 2πR = 28

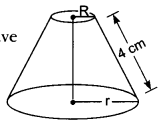
We have, slant height, l = 4 cm
Let R and r be the radii of two circular ends respectively. Therefore, we have
⇒ 2πR = 18 = πR = 9
⇒ 2πr = 6 = πr = 3
∴ Curved surface area of the frustum = (πR + πr)l
= (9 + 3) × 4 = 12 × 4 = 48 cm2
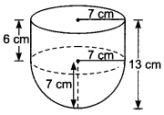
Here, radius of hemisphere = radius of cylinder = r cm = 7 cm
and height of cylinder, h = (13 – 7) cm = 6 cm
Now, inner surface area of the vessel
= Curved surface area of the cylindrical part + Curved surface area of hemispherical part = (2πrh + 2πr2) = 2πr (h + r)
= 2 × 227 × 7 (6 + 7)
= 2 × 22 × 13 = 572 cm2
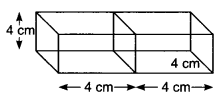
Let the length of each edge of the cube of volume 64 cm3 be x cm.
Then, Volume = 64 cm3
⇒ x2 = 64
⇒ x2 = 43
⇒ x = 4 cm
4 cm The dimensions of cuboid so formed are
l = Length = (4 + 4) cm = 8 cm
b = Breadth = 4 cm and h = Height = 4 cm
∴ Surface area of the cuboid = 2 (lb + bh + lh)
= 2 (8 × 4 + 4 × 4 + 8 × 4)
= 2 (32 + 16 + 32)
= 160 cm2
Radius of the hemisphere (R) = 72 cm
∴ Surface area of the solid after surmounting hemisphere
= 6l2 – πR2 + 2πR2 = 6l2 + πR2
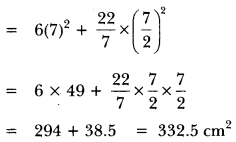
Volume of cuboid = 4.4 × 2.6 × 1 m2
Inner and outer radii of cylindrical pipe are 30 cm, (30 + 5) cm = 35 cm
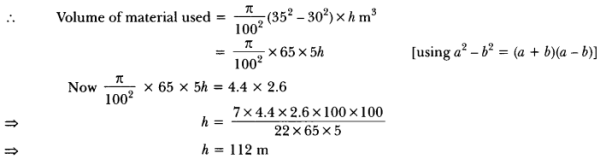
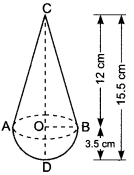
We have,
CD = 15.5 cm and OB = OD = 3.5 cm
Let r be the radius of the base of cone and h be the height of conical part of the toy.
Then, r = OB = 3.5 cm
h = OC = CD – OD = (15.5 – 3.5) cm = 12 cm

Edge of the cube = l = Diameter of the hemisphere
Therefore, radius of the hemisphere = l2
∴ Surface area of the remaining solid after cutting out the hemispherical
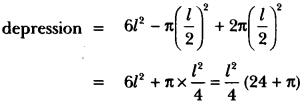
Long Answer :
Height of cone, h = 2(7) = 14 cm
Volume of solid = Vol. of hemisphere + Volume of cone
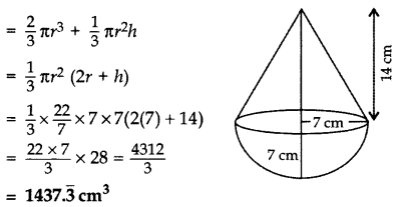

Internal radius of cylindrical pipe, r2 = 22 = 1 cm
Let the height of rises water, h1 = ?
Length of water flow in 1 second = 0.4 m
= 410 × 100 = 40 cm
∴ Length of water flow in 30 minutes, h2
= 40 × 60 × 30 = 72,000 cm
Volume of water in cylinder tank
= Volume of water flow from cylindrical pipe in half an hour
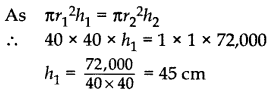
∴ Level of water in cylinder tank rises in half an hour, h1 = 45 cm


Case Study Answer:

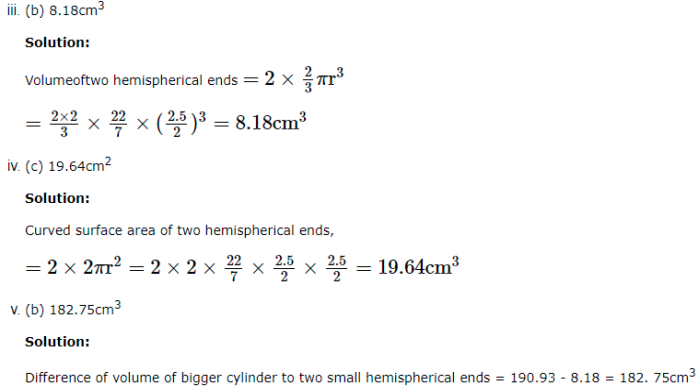


Assertion Reason Answer-
(c) A is true but R is false.
(a) Both A and R are true and R is the correct explanation of A.






