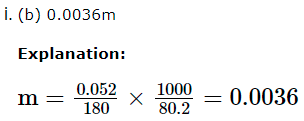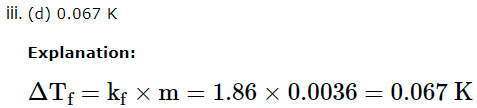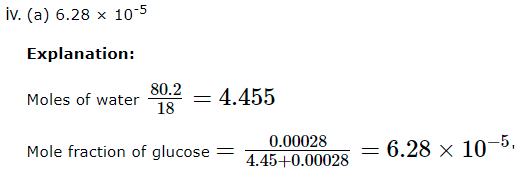SOLUTIONS

Introduction:

.

In this chapter, we will discuss about liquid solutions and their formation. This will be followed by studying the properties of solutions, like vapour pressure and colligative properties. We will begin with types of solutions and expressions for concentration of solutions in different units.

Thereafter, we will state and explain Henry’s law and Raoult’s law, distinguish between ideal and non-ideal solution and deviation of real solutions from Raoult’s law. We will also discuss abnormal colligative properties alongwith association and dissociation of solute.

Types of Solutions

.

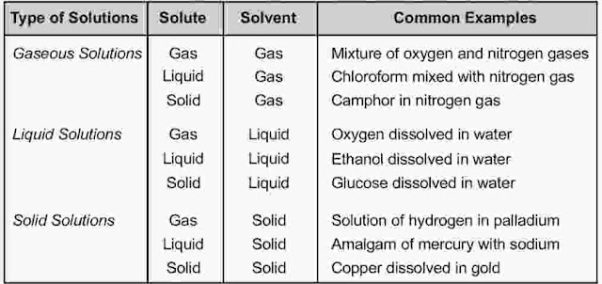
All the three states of matter (solid, liquid and gas) may behave either as solvent or solute. When a solution is composed of only two chemical substances, it is termed as binary solution. Depending upon the state of solute or solvent, binary solutions can be classified as

Some Important Definitions

.

Example– In a sugar syrup (liquid solution) containing 60% sugar (solid) and 40% water (liquid), water is termed as solvent, due to same physical state as that of solution.

Expressing the Strength of Solution

.

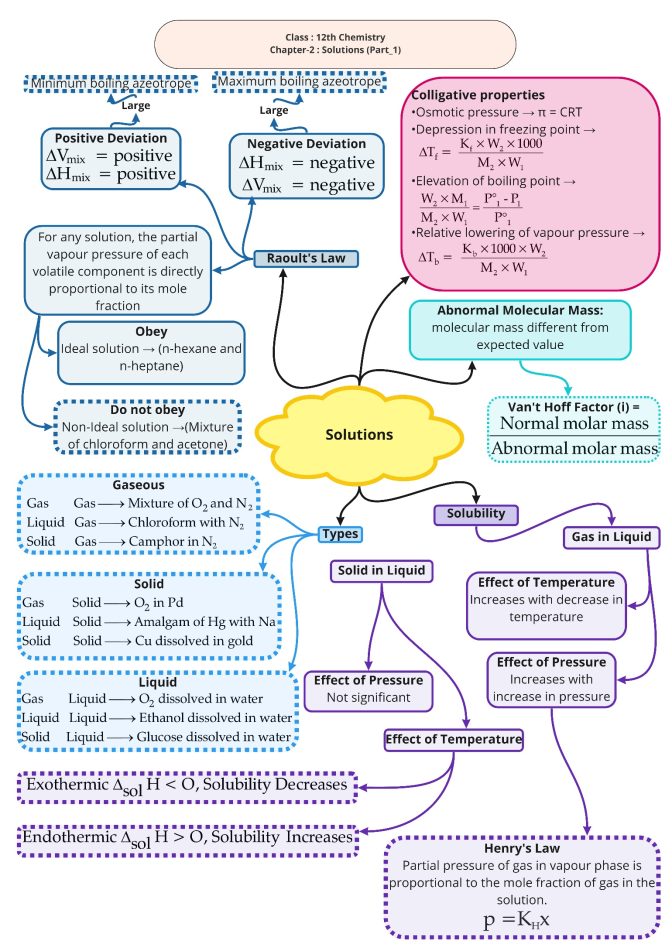
For a given solution the amount of solute dissolved per unit volume of solution is called concentration of solute. Strength of solution is the amount of solute in grams dissolved in one litre of solution. It is generally expressed in g/litre.

Other methods of expressing the strength of solution are:

$Mass\%ofsolute=\frac{Massofsolute}{Totalmassofsolution}\times 100$

$Mass\%ofsolvent=\frac{Massofsolvent}{Totalmassofsolution}\times 100$

$Volume\%ofsolute=\frac{Volumeofsolute}{Totalvolumeofsolution}\times 100$

$Volume\%ofsolvent=\frac{Volumeofsolvent}{Totalvolumeofsolution}\times 100$

$m=\frac{\left(Numberofmolesofsolute\right)}{\left(Massofsolvent\right\{inkg\left\}\right)}$

$M=\frac{\left(Numberofmolesofsolute\right)}{\left(Massofsoution\right\{inlitre\left\}\right)}$

$N=\frac{\left(Numberofgramequivalentsofsolute\right)}{\left(Volumeofsolution\right\{inlitre)}$

$Molefractionofsolute=\frac{\left(Numberofmolesofsolute\right)}{\left(Totalmolesofsolution\right)}$

$Molefractionofsolvent=\frac{\left(Numberofmolesofsolvent\right)}{\left(Totalmolesofsolution\right)}$

For a binary solution,

mole fraction of solute + mole fraction of solvent = 1.

It is defined in two ways

ppm = mass fraction × 10⁶

ppm = mole fraction × 10⁶

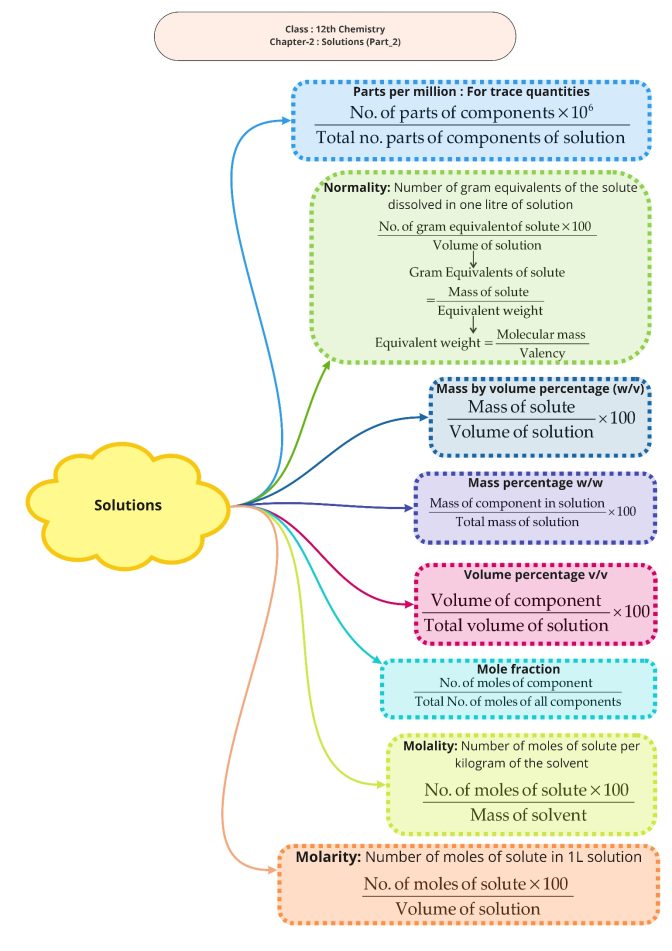
Solubility

.

Solubility of a substance is its maximum amount that can be dissolved in a specified amount of solvent at a specified temperature. It depends upon the nature of solute and solvent as well as temperature and pressure. Let us consider the effect of these factors in solution of a solid or a gas in a liquid.

A solute dissolves in a solvent if the intermolecular interactions are similar in them, i.e., like dissolves like. Polar solute dissolves in polar solvent and non-polar solute in non-polar solvent. For e.g., sodium chloride and sugar dissolves readily in water and napthalene and anthracene dissolves readily in benzene.

Solute + Solvent ⟶ Solution

  All gases are soluble in water as well as in other liquids to a greater or lesser extent. The solubility of a gas in liquid depends upon the following factors Nature of the gas, Nature of solvent, Temperature and Pressure.

Generally, the gases which can be easily liquified are more soluble in common solvents. For e.g., CO2 is more soluble than hydrogen or oxygen in water. The gases which are capable of forming ions in aqueous solutions are much more soluble in water than other solvents. For e.g., HCl and NH3 are highly soluble in water but not in organic solvents (like benzene) in which they do not ionize.

p = KH x,

KH = Henry’s law constant.

Applications of Henry’s law

Vapour Pressure of Solution

.

It is the pressure exerted by vapour on the surface layer of liquid at equilibrium between vapour and liquid.

Factors affecting Vapour Pressure

Raoult’s Law

.

According to Raoult’s law, for a solution of volatile liquids, the relative lowering of vapour pressure of solution is directly proportional to its mole fraction of dissolved solvent in solute.

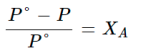
Ideal and Non-Ideal Solution 

The binary liquid-liquid solution may be classified into two types :

(1) Ideal solutions

(2) Non-ideal solutions

1) Ideal Solutions

An ideal solution may be defined as the solution which obeys Raoult’s law over the entire range of concentration.

a) Such solutions are formed by mixing two components which are identical in molecular size, in structure and have almost identical intermolecular forces.

b)The intermolecular interactions between the components (A – B attractions) are of same magnitude as the intermolecular interactions in pure components (A- A and B-B attractions).

According to Raoult’s law, the partial vapour pressure of two components of the solution may be given as :

pA = pA°xA

pB = pB°xB

Total pressure p is given by

p= pA +pB

p= pA°xA + pB°xB

The ideal solutions have also the following characteristics: 

1) Heat change on mixing is zero: Since there is no change in magnitude of the attractive forces in the two components present, the heat change on mixing i.e. ΔmixingH in such solutions must be zero.

2) Volume change on mixing is zero: In ideal solutions, the volume of the solution is the sum of the volumes of the components before mixing i.e. there is no change in volume on mixing or Δmixing V is zero.

The solutions generally tends to become ideal when they are dilute.

The characteristics of an ideal solution may be summed up as follows

(i) It must obey Raoult’s law.
(ii) Δmixing H should be zero.
(iii) Δmixing V should be zero.

Example of Ideal Solutions

(i) Benzene and toluene
(ii) n-hexane and n-heptane
(iii) Bromoethane and iodoethane
(iv) Chlorobenzene and bromobenene

Solutions which obey Raoult’s law are called ideal liquid solution.

Composition in Vapour Phase

The composition of vapour phase in equilibrium with the solution is determined by the partial pressure of the components. If y1and y2 are the mole fraction of the two components 1 and 2 respectively in the vapour phase, then according to Dalton’s law of partial pressures:

Partial pressure of a component =Mole fraction of the component x Total pressure

p1= y1 p

p2 =y2 p

In general, Pi = yi p total

Mole fraction of component 1 in vapour phase y1 = p1/p

Mole fraction of component 2 in vapour phase, y2 = p2 /p

Mole fraction of a component in vapour phase = 

Partial vapour pressure of component / Total Vapour Pressure

2) Non-Ideal Solutions

The solutions which do not obey Raoult’s law over the entire range of concentration are called non-ideal solutions. Therefore, for such solutions

pA ≠ pA° xA

pB ≠ pB° xB

The vapour pressure of such solutions is either higher or lower than that predicted by Raoult’s law.

In non-ideal solutions, there is a noticeable change in volume and heat energy when the two components are mixed.

Most of the solutions are non-ideal because they deviate from ideal behaviour to more or less extent.

Thus, for non-ideal solutions,

a) none of the components obey Raoult’s law over the entire composition range, i.e.

pA ≠ pA° xA and  pB ≠ pB° xB

b) (i) Δmixing H is not equal to zero

(ii) Δmixing V is not equal to zero

Ideal solution	Non-Ideal solution
The interactions between the components are similar to those in the pure components.	The interaction between the components are different from those of the purecomponents.
There is no enthalpy change on mixing. ΔmixingH =0	There is no enthalpy change on mixing. ΔmixingH ≠ 0
There is no volume change on mixing. Δmixing V =0	There is no volume change on mixing. Δmixing V ≠ 0
Each component obeys Raoult’s law at all temperatures and concentrations, pA = pA°xA  andpB = pB°xB	Their components do not obey Raoult’s law. They show positive and negative deviations from Raoult’s law. pA ≠ pA° xA and  pB ≠ pB° xB

.

Types of Non-ideal Solutions

Non-ideal solutions show positive and negative deviations from the ideal behaviour depending upon their nature.

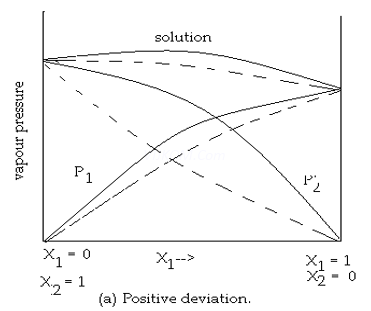
(1)  Non-Ideal solutions showing positive deviations from Raoult’s law

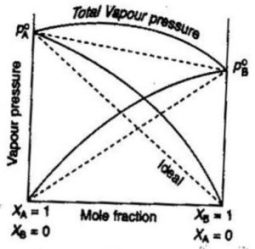
Consider a binary solution of two components A and B.

If the A-B interactions in the solutions are weaker than the A-A and B-B interactions in the two liquids forming the solution, then the escaping tendency of A and B types of molecules from the solution becomes more than from pure liquids. As a result, each component of solution has a partial vapour pressure greater than expected on the basis of Raoult’s law. The total vapour pressure will be greater than corresponding vapour pressure expected in case of ideal solution of the same composition. This type of behaviour of solution is described as positive deviations from Raoult’s law. 

pA >pA° xA  and

pB >pB° xB

The total vapour pressure,

p= pA+ pB is always greater than (pA° xA +  pB° xB )

Examples of solutions showing positive deviations are :

(i) Ethyl alcohol and cyclohexane
(ii) Acetone and carbon disulphide
(iii) Benzene and acetone
(iv) Carbon tetrachloride and choloroform
(v) Acetone and ethyl alcohol
(vi) Ethyl alcohol and water.

Explanation for positive deviations

In ethyl alcohol, the molecules are held together due to hydrogen bonding.When cyclohexane is added to ethyl alcohol, the molecules of cyclohexane tend to occupy the spaces between ethyl alcohol molecules. Consequently, some hydrogen bonds in alcohol molecules break and the attractive forces in alcohol molecules are weakened. The escaping tendency of alcohol and cyclohexane molecules from the solution increases. Consequently, the vapour pressure of the solution is greater than the vapour pressure as expected according to Raoult’s law.

(i) ΔmixingH is positive because energy is required to break A-A or B-B attractive forces.Therefore, dissolution process is endothermic.

(ii)Because of the decrease in the magnitude of intermolecular forces in solutions, the molecules will be loosely held and, therefore, there will be increase in volume on mixing. Thus, ΔmixingV will be positive.

(iii) Since the dissolution process in endothermic, heating will increase the solubility of such a solution.

(2) Non-Ideal solutions showing negative deviations from Raoult’s law.

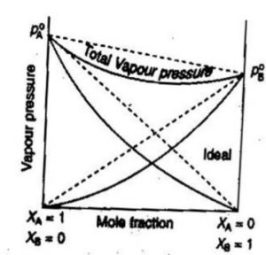
In such solutions, the A-B interactions are stronger than the A-A and B-B interactions present in the two liquids forming the solution. Due to stronger A-B interactions, the escaping tendency of A and B types of molecules from the solution becomes less than from pure liquids. Consequently, each component of the solution has a partial vapour pressure less than expected on the basis of Raoult’s law. As a result , the total vapour pressure becomes less than the corresponding vapour pressure expected in case of ideal solution.

pA < pA° xA  and

pB < pB° xB

p= pA+ pB is always less than (pA° xA +  pB° xB )

Examples of Negative Deviation

(i) Acetone and chloroform
(ii) Chloroform and diethyl ether
(iii) Chloroform and nitric acid
(iv) Acetone and aniline
(v) Water and nitric acid
(vi) Diethyl ether and chloroform.

Explanation for Negative Deviations

When acetone and chloroform are mixed there are new attractive forces due to intermolecular hydrogen bonding. Thus the attractive forces become stronger and the escaping tendency of each liquid from the solution decreases. Therefore, the vapour pressure of the solution is less than that expected for an ideal solution.

(i) ΔmixingH is negative because energy is released due to increase in attractive forces.Therefore, dissolution process is exothermic and heating the solution will decrease solubility.

(ii)Because of the increase in the magnitude of forces of attraction in solutions, the molecules will be loosely held more tightly. Therefore, there will be decrease in volume on mixing. Thus, ΔmixingV will be negative.

Difference between Ideal and Non-Ideal solution

Solution having positive deviation	Solution having negative deviation
A-B forces are less than A-A and B-B forces.	A-B forces are more than A-A and B-B forces.
pA >pA° xA  and pB >pB° xB	pA < pA° xA  and pB < pB° xB
ΔmixingH is positive	ΔmixingH is negative
Dissolution is endothermic	Dissolution is exothermic
Heating increases solubility	Heating decreases solubility
ΔmixingV will be positive.	ΔmixingV will be negative.

.

a) Some solution exhibit very large positive deviation from Raoult’s law that there is a maximum in the vapour pressure curve which is above the vapour pressure of either pure components.

For one of the intermediate composition, the total vapour pressure of such a solution will be the highest and the boiling point will be the lowest. At this point, the composition of liquid and vapour phase is same and the liquid mixture boils at constant temperature and remains unchanged in composition. Therefore, this liquid mixture distills over as if it is a pure liquid. Solution acquires the property of boiling at constant temperature and remains unchanged in composition.

The solutions (liquid mixtures) which boil at constant temperature and can distil unchanged in composition are called azeotropes or azeotropic mixtures. Thus, the azeotropes distil over as if it were pure liquids. These types of solutions are called minimum boiling azeotropes.

For example: Ethanol and water form minimum boiling azeotrope. It has maximum in the vapour pressure curve and hence a minimum in the boiling point diagram. In this boiling point diagram, we indicate the composition of the vapour phase by the upper curve and composition of the liquid phase by the lower curve.

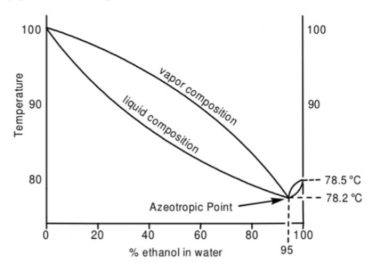
The boiling point diagram shows an azeotropic composition at x(H₂O)=0.056 and  x(C₂H₅OH) = 0.944 at a temperature.of 351 K (or 78°C) which is lower than that of pure ethanol 351.5 K (or 78.5°C) and water 378 K (or 100°C).

Fractional distillation of solutions lying on either side of this azeotropic composition is capable of separating them into at best, one pure component and a azeotropic mixture having the minimum boiling point.

b) In the case of solutions showing negative deviations, total vapour pressure becomes less than the corresponding ideal solution of same composition. The boiling points of such solutions are increased.

For one of the intermediate composition, the total vapour pressure will be the least and the boiling point will be the highest. At this composition, the solution also boils at constant temperature without a change in composition. This is also called azeotrope.

The solutions which show negative deviations from Raoult’s law are called maximum boiling azeotropes because they have a composition having maximum boiling point

For example: hydrochloric acid and water form maximum boiling point azeotrope at the composition x(H₂O)=0.889 and x (HCl)=0.111 (or 20.2% HCl) which boils at 381.6 K (or 108.6°C) which has higher than that of pure water.

Nitric acid (HNO₃) and water also form maximum boiling azeotrope. The azeotrope has the approximate composition 68% nitric acid and 32% water by mass with a boiling point of 393.5 K.

Thus, the azeotropes are liquid mixtures of definite composition, which boil at constant boiling point. These cannot be separated into pure components by fractional distillation. 

Colligative Properties

.

The properties of dilute solution which depends only on number of particles of solute (molecules or ions) present in the solution and not on their nature, are called colligative properties. The important colligative properties are;

According to Raoult’s law,

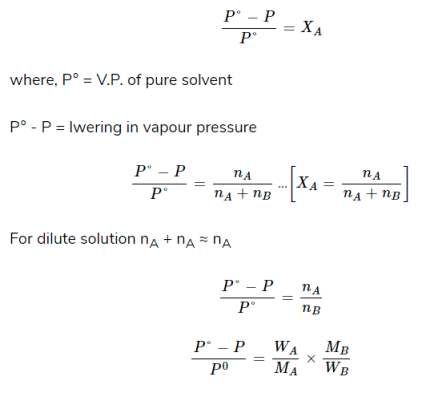
where, W_A = weight of solute

W_B = weight of solvent

M_A = molecular weight of solute

M_B = molecular weight of solvent

A liquid boils at the temperature at which its vapour pressure is equal to the atmospheric pressure. The boiling point of a solution of non-volatile solute is always higher than that of the boiling point of pure solvent in which the solution is prepared. Similar to lowering of vapour pressure, the elevation of boiling point also depends on the number of solute particles rather than their nature.

Let T° be the boiling point of pure solvent and T be the boiling point of solution. The increase in boiling point ΔTb = T – T° is known as elevation in boiling point.

For dilute solutions, the ΔT_b is directly proportional to the molal concentration of the solute in a solution. Thus

ΔT_b∝ m

ΔT_b = Kbm

K_b is molal elevation constant (Ebullioscopic constant). The unit of K_b is K kg mol^–1.

Substituting the value of molality in above equation, we get

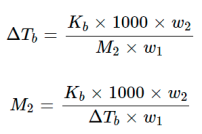
Where, w₁ = mass of solvent, w₂ = mass of solute and M₂ = molar mass of solute

Freezing point is the temperature at which vapour pressure of liquid phase becomes same as that of solid phase. The decrease in freezing point of a solvent on the addition of a non-volatile solute is known as depression in freezing point.

Let T° be the freezing point of pure solvent and T be the freezing point of solution. The decrease in freezing point ΔT_f = T° -T is known as depression in freezing point.

For dilute solutions, the ΔT_f is directly proportional to the molal concentration of the solute in a solution. Thus

ΔT_f∝ m

ΔT_f = Kf ⋅ m

Here K_f is molal depression constant or cryoscopic constant

Substituting the value of molality in above equation, we get

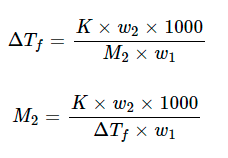
Where, w₁ = mass of solvent, w₂ = mass of solute and M₂ = molar mass of solute

Osmosis is the spontaneous flow of the solvent molecules from a less concentrated solution (dilute) to a more concentrated solution through a semi-permeable membrane. The driving force of osmosis is called osmotic pressure. Osmotic pressure may be defined as “the minimum excess pressure that has to be applied on the solution to prevent the osmosis”.

Osmotic pressure of a solution ∝ molar concentration of solute in that solution

π ∝ c

π = cRT

where, R = Gas constant = 0.0821 lit atm K^-1 mole^-1

T = Temperature

c = Molar concentration

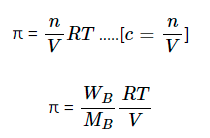
W_B = wt. of solute

M_B = Molar mass of solute

van’t Hoff Factor

To calculate the extent of association or dissociation, van’t Hoff in 1886 introduced a factor ‘i’ called van’t Hoff factor. van’t Hoff factor ‘i’ is defined as ratio of the experimental value of colligative property to the calculated value of colligative property.

$i.e.,i\frac{Experimentecolligativalproperties}{Calculatedecolligativproperties}$

Abnormal Molar Masses

Abnormal Molecular Masses

The accurate values of molar masses can be obtained only if the following two conditions are met.

(i) The solutions should be dilute

The solutions used for measuring colligative properties must not be too concentrated. In the concentrated solutions, the particles begin to interact with each other as well as with the solvent. As a result, the vapour pressure and therefore, other colligative properties depend upon the nature of the solute and not just on the number of solute particles.

(ii) The solute must not dissociate or associate in solution

The equations derived for measuring the colligative properties are for non-electrolyte solutes which do not undergo any dissociation or association in the solution.

Discrepancies in determination of molar mass arise when the solute dissociate or associate on dissolving in a solvent. This is because due to the association or the dissociation of the solute molecules in the solution, the number of molecules undergo a change.

The discrepancy in molar mass is called abnormal molar mass. The abnormal molar masses is due to association or dissociation of solute particles.

Association of Solute Particles

In certain solvents, generally non-polar, the solute molecules undergo association i.e. two, three or even more molecules exist in combination with each other to form bigger molecules. For example: suppose n simple molecules combine to form an associated molecule as:

nA ⇔ A_n

Therefore, the total number of molecules in solution become less than the number of molecules of the substance added and, therefore, colligative properties will be lower. Since the colligative properties are inversely proportional to the molar mass of the solute, the molar masses in such cases will be greater than the theoretical values.

For example: In benzene solvent, both ethanoic acid (acetic acid) and benzoic acid exist as dimers as:

2CH3COOH ⇔ (CH3COOH)2

2C6H5COOH ⇔ (C6H5COOH)2

The molar masses of ethanoic acid and benzoic acid have been found to be nearly 120 and 244 which are about double than their normal values of 60 and 122. The association of solute molecules in a solution is generally due to the hydrogen bonding between these molecules.

For example: benzoic acid and ethanoic acid exist as dimers due to the formation of hydrogen bonds. Due to association of ethanoic acid or benzoic acid, the ΔTf or ΔTb value will  be about half of the normal value. Therefore, the molar mass calculated on the basis of ΔT will be about twice the expected value.

Dissociation of Solute Molecules

Molecules of certain substances (acids, bases and salts) dissociate or ionise in a solvent to give two or more particles.

For example: AB dissociates to give double number of particles as:

AB ⇔  A+ + B–

The total number of particles increases in solution and, therefore, the colligative properties of such solutions will be large. Since colligative properties are inversely proportional to molar mass, the observed molar mass will be less than the theoretical value.

For example, KCl dissociates to give K+ and Cl– ions.

KCl ⇔ K+ + Cl–

If we dissolve 1 mol of KCl (74.5 g) in water, we expect 1 mol of K+ and 1 mol of Cl– ions to be produced in the solution. Therefore, there would be 2 mol of particles in the solution  instead of 1 mol. Consequently, the colligative properties would also be about double than expected.

For example: if we ignore interionic attraction, 1 mol of KCl in 1 kg of water would be expected to increase the boiling point by 2 X 0.52 K (Kb= 0.52 Km-1) = 1.04 K.

Van’t Hoff Factor

In 1886, Van’t Hoff introduced a factor called Van’t Hoff factor, i , to express the extent of association or dissociation of solutes in solution. It is the ratio of the normal and observed molar masses (or abnormal molar mass) of the solute, i.e.

$i=\frac{Normalmolarmass}{Observedmolarmass}$

In case of association, observed molar mass being more than the normal, the factor i has a value less than 1.

But in case of dissociation, the Van’t Hoff factor is more than 1 because the observed molar mass has a lesser value.

In case of solutes which do not undergo any association or dissociation in a solvent, the Van’t Hoff factor i will be equal to 1 because the observed and normal molar masses will be same.

Since the molar masses are inversely proportional to the colligative property. Van’t Hoff factor may also be expressed as:

$i=\frac{Observedcolligativeproperty}{Normalcollegativeproperty}$

Relative lowering in vapour pressure = i xsolute = Δp / p°

Elevation in boiling point , Δ Tb =i Kb  m

Depression in freezing point = Δ Tf = i Kf m

Osmotic pressure π = i cRT

Van’t Hoff Factor and Extent of Dissociation or Association in an Electrolytic Solution

Van’t Hoff factor can be used to calculate the extent of dissociation or association in terms of degree of dissociation or association of a substance in solution.

(i) Degree of dissociation: It is defined as the fraction of total substance that undergoes dissociation into ions, i.e.

Degree of dissociation = No. of moles of the substance dissociated / Total number of moles of the substance taken

Suppose a molecule of an electrolyte gives n ions after dissociation. Then if we start with 1 mole of the solute, and α is the degree of dissociation, then at equilibrium:

Number of moles of solute left undissociated =1-α

Number of moles of ions formed = nα

Total number of moles of particles 1-α+ nα

Van’t Hoff factor, i =

Observed number of moles of solute / Normal number of moles of solute

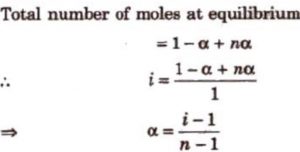
Knowing the value of i from observed molar mass and normal molar mass, degree of dissociation, α can be calculated.

For the electrolytes of the type AB, such as KCl, NaCl, etc,.the number of particles in solution i.e. n=2

For the electrolytes of the type AB, like CaCl₂, Ba(NO₃)2 etc, the value of n=2, so that

α = ( i-1 ) /2

(ii) Degree of association: It is defined as the fraction of total number of molecules which combine to form associated molecules, i.e.

$Degreeofassociation=\frac{No.ofmolesofthesubstanceassociated}{Totalnumberofmolesofsubstancetaken}$

For example: suppose n simple molecules of the solute associate to form the associated molecule A.

nA=  An

If we start with 1 mole of A and α is the degree of association, the concentration of the species after association is 

[An] = α/n

[A] =1-α

Total number of moles after association = 1-α+ α/n

Thus, the colligative properties will correspond to (1-α+ α/n) mole particles rather than one mole of particles.

Van’t Hoff factor, i , is : Observed number of moles of solute / Normal number of moles of solute

= 1-α + α/n / 1

= 1+ α (1/n -1)

α =( i-1 ) /( 1/n -1)

$I=\frac{Normalmolarmass}{Observedmolarmass}$

Knowing n the number of simple molecules which combine to give associated molecule, observed molar mass, degree of association(α) can be calculated.

.

.

.

.

Important Questions

Multiple Choice questions-

Question 1. Which of the following units is useful in relating concentration of solution with its vapour pressure?

(a) mole fraction

(b) parts per million

(c) mass percentage

(d) molality

Question 2. On dissolving sugar in water at room temperature, solution feels cool to touch. Under which of the following cases dissolution of sugar will be most rapid?

(a) Sugar crystals in cold water.

(b) Sugar crystals in hot water.

(c) Powdered sugar in cold water.

(d) Powdered sugar in hot water.

Question 3. At equilibrium the rate of dissolution of a solid solute in a volatile liquid solvent is

(a) less than the rate of crystallisation

(b) greater than the rate of crystallisation

(c) equal to the rate of crystallisation

(d) zero

Question 4. A beaker contains a solution of substance ‘A’. Precipitation of substance ‘A’ takes place when small amount of ‘A’ is added to the solution. The solution is ………………

(a) saturated

(b) supersaturated

(c) unsaturated

(d) concentrated

Question 5. Maximum amount of a solid solute that can be dissolved in a specified amount of a given liquid solvent does not depend upon .

(a) temperature

(b) nature of solute

(c) pressure

(d) nature of solvent

Question 6. Low concentration of oxygen in the blood and tissues of people living at high altitude is due to

(a) low temperature

(b) low atmospheric pressure

(c) high atmospheric pressure

(d) both low temperature and high atmospheric pressure

Question 7. Considering the formation, breaking and strength of hydrogen bond, predict which of the following mixtures will show a positive deviation from Raoult’s law?

(a) Methanol and acetone.

(b) Chloroform and acetone.

(c) Nitric acid and water.

(d) Phenol and aniline.

Question 8. Colligative properties depend on

(a) the nature of the solute particles dissolved in solution.

(b) the number of solute particles in solution.

(c) the physical properties of the solute particles dissolved in solution.

(d) the nature of solvent particles.

Question 9.Which of the following aqueous solutions should have the highest boiling point?

(o) 1.0 M NaOH

(b) 1.0 M Na₂SO₄

(c) 1.0 M NH₄NO₃

(d) 1.0 M KNO₃

Question 10. The unit of ebullioscopic constant is

(a) K kg mol^-1 or K (molality)^-1

(b) mol kg K^-1 or K^-1 (molality)

(c) kg mol^-1 K^-1 or K^-1 (molality)^-1

(d) K mol kg^-1 or K (molality)

Question 11.In comparison to a 0.01 M solution of glucose, the depression in freezing point of a 0.01 M MgCl₂ solution is ………..

(a) the same

(b) about twice

(c) about three times

(d) about six times

Question 12.An unripe mango placed in a concentrated salt solution to prepare pickle shrivels because ………..

(a) it gains water due to osmosis.

(b) it loses water due to reverse osmosis.

(c) it gains water due to reverse osmosis.

(d) it loses water due to osmosis.

Question 13. At a given temperature, osmotic pressure of a concentrated solution of a substance

(a) is higher than that of a dilute solution.

(b) is lower than that of a dilute solution.

(c) is same as that of a dilute solution.

(d) cannot be compared with osmotic pressure of dilute solution.

Question 14. Which of the following statements is false?

(a) Two different solutions of sucrose of same molality prepared in different solvents will have the same depression in freezing point.

(b) The osmotic pressure of a solution is given by the equation π = cRT (where c is the molarity of the solution).

(c) Decreasing order of osmotic pressure for 0.01 M aqueous solutions of barium chloride, potassium chloride, acetic acid and sucrose is BaC_l2> KCl > CH₃COOH > sucrose.

(d) According to Raoult’s law, the vapour pressure exerted by a volatile component of a solution is directly proportional to its mole fraction in the solution.

Question 15.he values of Van’t Hoff factors for KCl, NaCl and K₂SO₄, respectively, are

(a) 2, 2 and 2

(b) 2, 2 and 3

(c) 1,1 and 2

(d) 1, 1 and 1

Very Short Question:

Question 1. Define the term – solubility?

Question 2. What is the effect of pressure on solubility of a gas?

Question 3. State Henry’s Law.

Question 4. State Raoult’s Law.

Question 5. What are the factors on which vapour pressure depends?

Question 6. The vapour pressure of solvent gets lowered, when a non- volatile solute isadded to it. Why?

Question 7. Name two ways by which vapour pressure of a liquid can be lowered.

Question 8. Define solution?

Question 9. Define the following terms:

(a) Molality

(b) Molarity

Question 10. How does change in temperature changes the molarity and molality values?

Short Questions:

Question 1 Find the molality and molarity of a 15% solution of H₂SO₄ when its density is

Question 2. Calculate the mole fraction of ethanol and water in a sample of rectified spirit which contains 46% ethanol by mass?

Question 3. Calculate the % composition in terms of mass of a solution obtained by mixing 300g of a 25% & 400 g of a 40% solution by mass?

Question 4. One litre of sea water weight 1030g and contains about of dissolved Calculate the concentration of dissolved oxygen in ppm?

Question 5. The density of 85% phosphoric acid is. What is the volume of a solution that contains 17g of phosphoric acid?

Question 6. Define the term azeotrope?

Question 7. Obtain a relationship between relative lowering of vapour pressure and mole fraction of solute?

Question 8. Draw the graphs of both deviations from ideal behaviours?

Question 9. A weak electrolyte AB in 5% dissociated in aqueous solution? What is the freezing point of a 0.10 molar aqueous solution of AB? K_f = 1.86 deg/molal?

Question 10. Henry’s law constant for the molality of methane in benzene at 298 K is . Calculate the solubility of methane in benzene at 298 K under 760 mm Hg.

Long Questions:

Question 1.

The vapour pressure of at is 854 mm Hg .A solution of 2.0g sulphur in 100g of has a vapour pressure of 848.9 mm Hg .Calculate the formulaof sulphur molecule

Question 2. Calculate the mass percentage of benzene (C₆H₆) and carbon tetrachloride (CCl₄) if 22 g of benzene is dissolved in 122 g of carbon tetrachloride.

Question 3. Calculate the mole fraction of benzene in solution containing 30% by mass in carbon tetrachloride.

Question 4.Calculate the molarity of each of the following solutions: (a) 30 g of . in 4.3 L of solution (b) 30 mL of 0.5 M H₂SO₄diluted to 500mL.

Question 5.Calculate (a)molality (b)molarity and (c)mole fraction of KI if the density of 20% (mass/mass) aqueous KI is

Assertion and Reason Questions:

1.In these questions, a statement of assertion followed by a statement of reason is given. Choose the correct answer out of the following choices.

Assertion: Camphor is used as a solvent in the determination of molecular masses of naphthalene, anthracene, etc.

Reason: Camphor has high molal elevation constant.

  2.In these questions, a statement of assertion followed by a statement of reason is given. Choose the correct answer out of the following choices.

Assertion: Reverse osmosis is used in the desalination of sea water.

Reason: When pressure more than osmotic pressure is applied, pure water is squeezed out of the sea water through the membrane.

Case Study Questions:

1.Read the passage given below and answer the following questions:

The solubility of gases increases with increase of pressure. William Henry made a systematic investigation of the solubility of a gas in a liquid. According to Henry’s law “the mass of a gas dissolved per unit volume of the solvent at constant temperature is directly proportional to the pressure of the gas in equilibrium with the solution”. Dalton during the same period also concluded independently that the solubility of a gas in a ti quid solution depends upon the partial pressure of the gas. If we use the mole fraction of gas in the solution as a measure of its solubility, then Henry’s law can be modified as “the partial pressure of the gas in the vapour phase is directly proportional to the mole fraction of the gas in the solution”

The following questions are multiple choice questions. Choose the most appropriate answer:

2.Read the passage given below and answer the following questions

Few colligative properties are:

A solution of glucose is prepared with 0.052 g at glucose in 80.2 g of water.(KJ = 1.86K kg mol^-1 and K_b = 5.2K kg mol^-1)

The following questions are multiple choice questions. Choose the most appropriate answer:

Answers key

MCQ answers:

Very Short Answers:

1) Temperature of the liquid. 2) Nature of the liquid.

(b) Molarity (M) = Number of moles of solute dissolved in one litre of solution.

Short Answers:

Volume = mass/density
.

.

Molarity = 
.

= .
Molality = 
.

  

= 1.8 M.

Mass of ethanol = 46g

Mass of water = 100 – 46 = 54g

Mole fraction of ethanol,

=

Mole fraction of water = 1-0.25 = 0.75

Mole fraction of water = 1-0.25 = 0.75

mass of solute in 400g of 40%

= 

Total mass of solute = 160+75 = 235g

Total mass of solution = 400+300 = 700g
.

Mass% of solute = 

= 

Mass % of solvent = 100 – 33.57 = 66.43%

mass of 
ppm of in 1030 g sea water =   

= 
.

5. Answer :

Ans. 85g phosphoric acid is present in 100g of solution.

17g of phosphoric acid is present in

 

Volume of 17g of 85% acid = 
.

= 

6. Answer

A solution at certain concentration when continues to boil at constant temperature without change in its composition in solution & in vapour phase is called an azeotrope.

7. Answer:

According to Raoult’s Law –

= 
Relative lowering of vapour pressure.

8. Answer:

9. Answer :

Degree of dissociation of AB = .
AB   A⁺ + B^–
M             0       0
No. of moles dissolved
No. of moles after dissociations  

m (1-)   m  m

0.1 (1 – 0.05)   

Total moles = 0.1(1−0.05) + + 

= 0.095 + 0.005 + 0.005 = 0.105m

= 0.1953 deg.

p = 760 mm Hg

According to Henry’s law,



= 
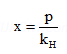
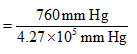
= (approximately)
Hence, the mole fraction of methane in benzene is .

Long Answers:

 = 854 mm, ,

= 

= 
= 254.5 g/mol.
.

Let the formula = Sx
.

X= 
=7.95
=8.
= Formula = S₈

2. Answer:

Mass percentage of 

=15.28%

Mass percentage of =
.

.

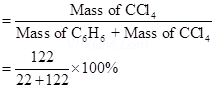
=84.72%
.

Alternatively,
.

Mass percentage of = (100 – 15.28) %
.

=84.72%

3. Answer:

Let the total mass of the solution be 100 g and the mass of benzene be 30g.

∴ Mass of carbon tetrachloride = (100 – 30) g
= 70 g
Molar mass of benzene () = (612 + 6) 
= 78 
∴ Number of moles of 
.

= 0.3846 mol
.

Molar mass of carbon tetrachloride ( ) = 112 + 4355
= 154 
∴Number of moles of 
.

= 0.4545 mol
Thus, the mole fraction of is given as:
.

.

 
.

= 0.458

4. Answer:

Molarity is given by:

(a) Molar mass of 59 + 2 (14 + 3 16) + 618

= 291 

Therefore, Moles of 
= 0.103 mol
Therefore, molarity 
.

= 0.023 M

(b) Number of moles present in 1000 mL of 0.5 M 
∴Number of moles present in 30 mL of 0.5 M

= 0.015 mol

Therefore, molarity= 0.03 M

5. Answer:

(a) Molar mass of KI = 39 + 127 = 166 
20% (mass/mass) aqueous solution of KI means 20 g of KI is present in 100 g of solution.
That is,
20 g of KI is present in (100 – 20) g of water = 80 g of water

Therefore, molality of the solution=

= 1.506 m
= 1.51 m (approximately)

(b) It is given that the density of the solution = 

Therefore, Volume of 100 g solution = 

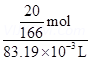= 83.19 mL
= 

Therefore, molarity of the solution = 

(c) Moles of KI = 

Moles of water = 

.

Therefore, mole fraction of KI =
=

= 0.0263

Assertion and Reason Answers:

1. (c) Assertion is correct statement but reason is wrong statement.

Explanation:

Camphor has high molal depression constant.

2. (a) Assertion and reason both are correct statements and reason is correct explanation for assertion.

Explanation:

If a pressure larger than the osmotic pressure is applied to the solution side, the pure solvent flows out of the solution to the solvent through semi-permeable membrane and this phenomenon is called reverse osmosis.

Case Study Answers:

1. Answer :

2. Answer :