
REAL NUMBER
Answer Key-
Multiple Choice questions-
Very Short Answer :
Smallest prime number = 2
So, HCF (4, 2) = 2
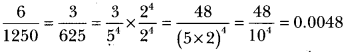
This representation will terminate after 4 decimal places.
⇒ 1800 = 12 × LCM
⇒ LCM =180012 = 150.
Therefore, remainder in both cases are same.
![]()
Since the denominator has 3 as its factor.
∴1730 is a non4ermznatlng decimal.
a = 3q + r, where O r < 3 and r is an integer.
Therefore, the values of r can be 0, 1 or 2.
Short Answer :
of 4n is 2. Also, we know from the fundamental theorem of arithmetic that the prime factorization of each number is unique.
∴ 4n can never end with 0.
9q2 = 3m, 9q2 + 6q + 1 = 3(3q2+ 2q) + 1 = 3m + 1,
9q2 + 12q + 4 = 3(3q2+ 4q + 1) + 1 = 3m + 1.
Now, since 616 > 32, we apply division lemma to 616 and 32.
We have, 616 = 32 × 19 + 8
Here, remainder 8 ≠ O. So, we again apply division lemma to 32 and 8.
We have, 32 = 8 × 4 + O
Here, remainder is zero. So, HCF (616, 32) = 8
Hence, maximum number of columns is 8.
12 22 × 3, 15 = 3 × 5 and 21 = 3 × 7
Therefore, the HCF of these integers is 3.
22, 31, 51 and 71 and are the greatest powers involved in the prime factors of 12, 15 and 21.
So, LCM (12, 15, 21) = 22 × 31 × 51 × 71 = 420.
Thus, LCM (26, 91) = 2 × 7 × 13 = 182
HCF (26, 91) = 13
Now, LCM (26, 91) × HCF (26, 91) = 182 × 13 = 2366
and Product of the two numbers = 26 × 91 = 2366
Hence, LCM × HCF = Product of two numbers.
(ii) 144 = 24 × 32 and 198 = 2 × 32 × 11
∴ LCM(198,144)24 × 32 × 11 = 1584
HCF(198, 144) = 2 × 32 = 18
Now, LCM (198, 144) × HCF (198, 144) = 1584 × 18 = 28512
and product of 198 and 144 = 28512
Thus, product of LCM (198, 144) and HCF (198, 144)
= Product of 198 and 144.
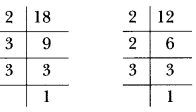
Therefore, LCM of 18 and 12 = 22 × 32 = 36
So, they will meet again at the starting point after 36 minutes.
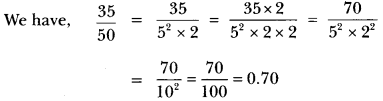
(ii)
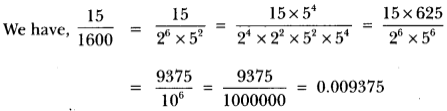
then x = 0.3178178178 … … (i)
10x = 3.178178178 … …(ii)
10000x = 3178.178178… …(iii)
On subtracting (ii) from (iii), we get
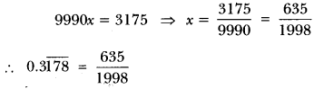
Case – I When n = (4q + 1)
In this case n2 – 1 = (4q + 1)21 = 16q2 + 8q = 8q(2q + 1)
which is clearly divisible by 8.
Case – II When n = (4q + 3)
In this case, we have
n22 = (4q + 3)2 – 1 = 16q2 + 24q + 8 = 8(2q2+ 3q + 1)
which is clearly divisible by 8.
Hence (n2 – 1) is divisible by 8.
And x + 14 = 600 ⇒ 15x = 600 ⇒ x = 40
Then HCF = 40 and LCM = 14 × 40 = 560
∵ LCM × HCF = Product of the numbers
560 × 40 = 280 × Second number Second number = 560×40280= 80
Then other number is 80.
Yes, value of x can be found without finding value of y or z as
x = 2 × 2 × 2 × 17 which arc prime 1tctors of x.
integer q ≥ O and O ≤ r < 6.
i.e., the possible remainders are 0, 1, 2, 3, 4, 5.
1’hus,a canbeoftheform6q,or6q + I,or6q + 2,orßq + 3,ör6q + 4,
or 6q + 5, where q is some quotient.
Since a. is odd integer, so a cannot be of the form , or + 2, or 6q + 4, (since they are even).
Thus, a is of the form 6q + 1, 6q + 3, or 6q + 5, where q is some integer.
Hence, any odd positive integer is of the form 6q + 1 or 6q -1- 3 or 6q + 5, where q is sorne integer.
(ii) We have, −0.16 a non-terminating but repeating decimal expansion. So it is rational.
Let x = −0.16
Then, x = 0.1616… (i)
100×16.1616… ..(ii)
On subtracting (i) from (ii), we get
100x – x = 16.1616 – 0.1616
⇒ 99x = 16 ⇒ x =1699=pq
The denominator (q) has factors other than 2 or 5.
Long Answer :
Then by Euclid’s division algorithm, corresponding to the positive integers a and 3 there exist
non-negative integers q and r such that
a = 3q + r where 0 ≤ r <3
a2 = 9q2 + 6qr + r2 ….(i) 0 ≤ r <3
Case – I: When r = 0 [putting in (i)]
a2 = 9q2 = 3(3q2) = 3m where m = 3q2
Case – II: r = 1
a2 = 9q2 + 6q + 1 = 3(3q2 + 2q)+ 1 = 3m + 1 where m = 3q2 + 2q
Case – III: r = 2
a2 = 9q2 + 12 + 4 = 3(3q2 + 4q + 1) + 1 = 3m + 1 where m = (3q2 + 4q + 1)
Hence, square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Therefore, n = 3q + r, where r = 0, 1, 2
n = 3q or n = 3q + 1 or n = 3q + 2
Case (i) if n = 3q, then n is divisible by 3, n + 2 and n +. 4 arc not divisible by 3.
Case (ii) if 71 = 3q + 1 then n + 2 = 3q + 3 = 3(q + 1), which is divisible by 3 and
n + 4 = 3q + 5, which is not divisible by 3.
So, only (n + 2) is divisible by 3.
Case (iii) If n = 3q + 2, then n + 2 = 3q + 4, which is not divisible by 3 and
(n + 4) = 3q + 6 = 3(q + 2), which is divisible by 3.
So, only (n + 4) is divisible by 3.
Hence one and only one out of n, (n + 2), (n + 4), is divisible by 3.
We have, 960 = 432 × 2 + 96
Since the remainder 96 ≠ 0, so we apply the division lemma to 432 and 96.
We have, 432 = 96 × 4 + 48
Again remainder 48 ≠ 0 so we again apply division lemma to 96 and 48.
We have, 96 = 48 × 2 + O
The remainder has now become zero. So our procedure stops.
Since the divisor at this stage is 48.
Hence, HOE of 960 and 432 is 48.
i.e., HCF (960, 432) = 4H
(ii) Since 12576 > 4052, we apply the division lemma to 12576 and 4052, to get
12576 = 4052 × 3 + 420
Since the remainder 420 ≠ 0, we apply the division lemma to 4052 and 420, to get
4052 = 420 × 9 + 272
We consider the new divisor 420 and the new remainder 272, and apply the division lemma to get
420 = 272 × 1 + 148
We consider the new divisor 272 and the new remainder 148, and apply the division lemma to get
272 = 148 × 1 + 124
We consider the new divisor 148 and the new remainder 124, and apply the division lemma to get
148 = 124 × 1 + 24
We consider the new divisor 124 and the new remainder 24, and apply the division lemma to get
124 = 24 × 5 + 4
We consider the new divisor 24 and the new remainder 4, and apply the division lemma to get
24 = 4 × 6 + O
The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.
30 = 2 × 3 × 5; 72 = 23 × 32 and 432 = 24 × 33
Here, 2’ and 31 are the smallest powers of the common factors 2 and 3 respectively.
So, HCF (30, 72, 432) = 21 × 31 = 2× 3 = 6
Again, 2, 33 and 51 arc the greatest powers of the prime factors 2, 3 and 5 respectively.
So, LCM (30, 72, 432) = 24 × 33 × 51 = 2160
HCF × LCM = 6 × 2160 = 12960
Product of numbers = 30 × 72 × 432 = 933120 .
Therefore, HCF × LCM ≠ Product of the numbers.
Then, there exist co-prime positive integers and such that
√7 = ab , b ≠ 0
So, a = √7 b
Squaring both sides, we have
a2 = 7b2 …… (i)
⇒ 7 divides a2 ⇒ 7 divides a
So, we can write
a = 7c (where c is an integer)
Putting the value of a = 7c in (i), we have
49c2 = 7b2 72 = b2
It means 7 divides b2 and so 7 divides b.
So, 7 is a common factor of both a and b which is a contradiction.
So, our assumption that √7 is rational is wrong.
Hence, we conclude that √7 is an irrational number.
So, 5 – √3 may be written as
5 – √3 = pq, where p and q are integers, having no common factor except 1 and q ≠ 0.
⇒ 5 – pq = √3 ⇒ √3 = 5q−pq
Since 5q−pq is a rational number as p and q are integers.
∴ √3 is also a rational number which is a contradiction.
Thus, our assumption is wrong.
Hence, 5 – √3 is an irrational number.
we have, 2160 847 × 2 + 466
Since remainder 466 ≠ 0. So, we apply the division lemma to 847 and 466
847 = 466 × 1+ 381
Again remainder 381 ≠ 0. So we again apply the division lemma to 466 and 381.
466 = 381 × 1 + 85
Again remainder 85 ≠0. So, we again apply the division lemma to 381 and 85
381 = 85 × 4 + 41
Again remainder 41 ≠ 0. So, we again apply the division lemma to 85 and 41.
85 = 41 × 2 + 3
Again remainder 3 ≠ 0. So, we again apply the division lemma to 4 1 and 3.
41 = 3 × 13 + 2
Again remainder 2 ≠ 0. So, we again apply the division lemma to 3 and 2.
3 = 2 × 1 + 1
Again remainder 1 ≠ 0. So, we apply division lemma to 2 and 1
2 = 1 × 2 + 0
The remainder now becomes O. So, our procedure stops.
Since the divisor at this stage is 1.
Hence, HCF of 847 and 2160 is 1 and numbers are co-prime.

⇒ √n−1is also perfect. square of positive integer From (A) and (B)
√n+1 and √n−1 are perfect squares of positive integer. It contradict the fact that two perfect squares differ at least by 3.
Hence, there is no positive integer n for which √n−1 + √n+1 is rational.
Similarly, required positive integer is a Íctor of 436 – 11 = 425 and 542 – 15 = 527
Clearly, the required number is the HCF of 391, 425 and 527.
Using the factor tree, we get the prime factorisations of 391, 425 and 527 as follows:
391 = 17 × 23, 425 52 × 17 and 527 17 × 31
∴ HCF of 391, 425, and 527 is 17.
Hence, the required number = 17.
Case Study Answers:
Solution:
For a number to end in zero it must be divisible by 5, but 4n = 22n is never divisible by 5. So, 4n never ends in zero for any value of n.
Solution:
We know that product of two rational numbers is also a rational number.
So, a2 = a × a = rational number.
a3 = a2 × a = rational number.
a4 = a3 × a = rational number.
………………………………..
………………………………..
an = an-1 × a = rational number.
Solution:
Let x = 2m + 1 and y = 2k + 1
Then x2 +y2 = (2m + 1)2 + (2k + 1)2
= 4m2 + 4m + 1 + 4k2 + 4k + 1
= 4(m2 + k2 + m + k) + 2
So, it is even but not divisible by 4.
Solution:
Let three consecutive positive integers be n, n + 1 and n + 2.
We know that when a number is divided by 3, the remainder obtained is either 0 or 1 or 2.
So, n = 3p or 3p + 1 or 3p + 2, where pis some integer.
If n = 3p, then 2 is divisible by 3.
If n = 3p + 1, then n + 2 = 3p + 1 + 2 = 3p + 3 = 3(p + 1) is divisible by 3.
If n = 3p + 2, then n + 1 = 3p + 2 + 1 = 3p + 3 = 3(p + 1) is divisible by 3.
So, we can say that one of the numbers among n, n + 1 and n + 2 is always divisible by 3.
Solution:
Any odd number is of the form of (2k + 1), where k is any integer.
So, n2 – 1 = (2k + 1)2 – 1 = 4k2 + 4k
For k = 1, 4k2 + 4k = 8, which is divisible by 8.
Similarly, for k = 2, 4k2 + 4k = 24, which is divisible by 8.
And fork= 3, 4k2 + 4k = 48, which is also divisible by 8.
So, 4k2 + 4k is divisible by 8 for all integers k, i.e., n2 – 1 is divisible by 8 for all odd values of n.
Solution:
Here 80 = 24 × 5, 85 = 17 × 5
and 90 = 2 × 32 × 5
L.C.M of 80, 85 and 90 = 24 × 3 × 3 × 5 × 17 = 12240
Hence, the minimum distance each should walk when they at first time is 12240cm.
Solution:
Here 594 = 2 × 33 × 11 and 189 = 33 × 7
HCF of 594 and 189 = 33 = 27
Hence, the maximum number of columns in which they can march is 27.
Solution:
Here 768 = 28 × 3 and 420 = 22 × 3 × 5 × 7
HCF of 768 and 420 = 22 × 3 = 12
So, the container which can measure fuel of either tanker exactly must be of 12 litres.
Solution:
Here, Length = 825cm, Breadth = 675cm and Height = 450cm
Also, 825 = 5 × 5 × 3 × 11, 675 = 5 × 5 × 3 × 3 × 3 and 450 = 2 × 3 × 3 × 5 × 5
HCF = 5 × 5 × 3 = 75
Therefore, the length of the longest rod which can measure the three dimensions of the room exactly is 75cm.
Solution:
LCM of 8 and 12 is 24.

Assertion Reason Answer-






