https://makemynotes.in/real-numbers/

Real Numbers

Euclid’s Division Lemma:

Given positive integers a and b, there exists unique integers q and r satisfying a = bq + r, where 0 ≤ r < b

Lemma is a proven statement used for proving another statement.

Euclid’s Division Lemma states that given two integers a and b, there exists a unique pair of integers q and r such that a = b × q + r and 0 ≤ r < b.

This lemma is essentially equivalent to: dividend = divisor × quotient + remainder

In other words, for a given pair of dividend and divisor, the quotient and remainder obtained are going to be unique.

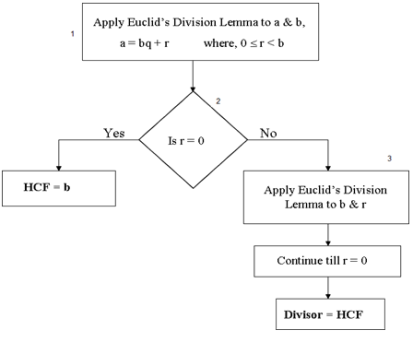
Euclid’s Division Algorithm:

An algorithm is a series of well defined steps which gives a procedure for solving a type of problem.

This algorithm is a technique to compute the H.C.F of two given positive integers.

According to this algorithm, the HCF of any two positive integers ‘a’ and ‘b’, with a > b, is obtained by following the steps given below:

Step 1: Apply Euclid’s division lemma, to ‘a’ and ‘b’, to find q and r, such that a = bq + r, 0 ≤ r < b.

Step 2: If r = 0, the HCF is b. If r ≠ 0, apply Euclid’s division lemma to b and r.

Step 3: Continue the process till the remainder is zero. The divisor at this stage will be HCF (a, b). Also, note that HCF (a, b) = HCF (b, r).

Euclid’s Division Algorithm can be summarized as follows:

Euclid’s Division Algorithm is stated for only positive integers but it can be extended for all integers except zero, i.e., b ≠ 0.

Consider two numbers 78 and 980 and we need to find the HCF of these numbers. To do this, we choose the largest integer first, i.e. 980 and then according to Euclid Division Lemma, a = bq + r where 0 ≤ r < b;

980 = 78 × 12 + 44

Now, here a = 980, b = 78, q = 12 and r = 44.

Now consider the divisor 78 and the remainder 44, apply Euclid division lemma again.

78 = 44 × 1 + 34

Similarly, consider the divisor 44 and the remainder 34, apply Euclid division lemma to 44 and 34.

44 = 34 × 1 + 10

Following the same procedure again,

34 = 10 × 3 + 4

10 = 4 × 2 + 2

4 = 2 × 2 + 0

As we see that the remainder has become zero, therefore, proceeding further is not possible. Hence, the HCF is the divisor b left in the last step. We can conclude that the HCF of 980 and 78 is 2.

Let us try another example to find the HCF of two numbers 250 and 75. Here, the larger the integer is 250, therefore, by applying Euclid Division Lemma a = bq + r where 0 ≤ r < b, we have

a = 250 and b = 75

⇒ 250 = 75 × 3 + 25

By applying the Euclid’s Division Algorithm to 75 and 25, we have:

75 = 25 × 3 + 0

As the remainder becomes zero, we cannot proceed further. According to the algorithm, in this case, the divisor is 25. Hence, the HCF of 250 and 75 is 25.

Real Numbers:

The numbers which can be represented in the form

\frac{p}{q},

of where p and q are integers and q ≠ 0 are called Rational numbers.

Any number that cannot be expressed in the

\frac{p}{q}

, form of , where p and q are integers and q ≠ 0 are called Irrational numbers.

There are more irrational numbers than rational numbers between two consecutive numbers.

Rational and Irrational numbers together constitute Real numbers.

Properties of Irrational numbers:

i.The Sum, Difference, Product and Division of two irrational numbers need not always be an irrational number.

ii.Negative of an irrational number is an irrational number.

iii.Sum of a rational and an irrational number is irrational.

iv.Product and Division of a non-zero rational and irrational number is always irrational.

Fractions:

Terminating fractions are the fractions which leaves remainder 0 on normal division.

Recurring fractions are the fractions which never leave a remainder 0 on normal division.

Properties related to prime numbers:

If p is a prime and divides a², then p divides a, where ‘a’ is a positive integer.

If p is a prime, then

\sqrt{p}

is an irrational number.

A number ends with the digit zero if and only if it has 2 and 5 as two of its prime factors.

1.Decimal Expansion:

The decimal expansion of rational number is either terminating or non-terminating recurring (repeating).

If the decimal expansion of rational number terminates, then we can express the number in the form of

\frac{p}{q}

, where p and q are co-prime, and the prime factorization of q is of the form 2ⁿ5^m, where n and m are non negative integers.

If

x = \frac{p}{q}

is a rational number, such that the prime factorization of q is of the form 2ⁿ5^m, where n, m are non-negative integers. Then, x has a decimal expansion which terminates.

If the denominator of a rational number is of the form 2ⁿ5^m, then it will terminate after n places if n > m or after m places if m > n.

The decimal expansion of an irrational number is non-terminating, non-recurring.

Fundamental Theorem of Arithmetic:

Every composite number can be expressed (factorized) as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur.

The procedure of finding HCF (Highest Common Factor) and LCM (Lowest Common Multiple) of given two positive integers a and b:

i.Find the prime factorization of given numbers.

ii.HCF (a, b) = Product of the smallest power of each common prime factors in the numbers.

iii.LCM (a, b) = Product of the greatest power of each prime factors, involved in the numbers.

Fundamental Theorem of Arithmetic states that every integer greater than 1 is either a prime number or can be expressed in the form of primes. In other words, all the natural numbers can be expressed in the form of the product of its prime factors. To recall, prime factors are the numbers which are divisible by 1 and itself only. For example, the number 35 can be written in the form of its prime factors as:

35 = 7 × 5

Here, 7 and 5 are the prime factors of 35

Similarly, another number 114560 can be represented as the product of its prime factors by using prime factorization method,

114560 = 27 × 5 × 179

So, we have factorized 114560 as the product of the power of its primes.

Therefore, every natural number can be expressed in the form of the product of the power of its primes. This statement is known as the Fundamental Theorem of Arithmetic, unique factorization theorem or the unique-prime-factorization theorem.

Proof for Fundamental Theorem of Arithmetic: In number theory, a composite number is expressed in the form of the product of primes and this factorization is unique apart from the order in which the prime factor occurs.

From this theorem we can also see that not only a composite number can be factorized as the product of their primes but also for each composite number the factorization is unique, not taking into consideration order of occurrence of the prime factors.

In simple words, there exists only a single way to represent a natural number by the product of prime factors. This fact can also be stated as:

The prime factorization of any natural number is said to be unique for except the order of their factors.

In general, a composite number “a” can be expressed as,

a = p₁ p₂ p₃ ………… p_n, where p₁, p₂, p₃ ………… p_n are the prime factors of a written in ascending order i.e. p₁ ≤ p₂ ≤ p₃ ………… ≤p_n.

Writing the primes in ascending order makes the factorization unique in nature.

Relationship between HCF and LCM of two numbers:

If a and b are two positive integers, then HCF (a, b) × LCM (a, b) = a × b

Relationship between HCF and LCM of three numbers:

$L C M (p, q, r) = \frac{p . q . r . H C F (p, q, r)}{H C F (p, q) . H C F (q, r) . H C F (p, r)}$

$H C F (p, q, r) = \frac{p . q . r . L C M (p, q, r)}{L C M (p, q) . L C M (q, r) . L C M (p, r)}$

Method of Finding LCM

In Mathematics, the LCM of any two is the value that is evenly divisible by the two given numbers. The full form of LCM is Least Common Multiple. It is also called the Least Common Divisor (LCD). For example, LCM (4, 5) = 20. Here, the LCM 20 is divisible by both 4 and 5 such that 4 and 5 are called the divisors of 20.

LCM is also used to add or subtract any two fractions when the denominators of the fractions are different. While performing any arithmetic operations such as addition, subtraction with fractions, LCM is used to make the denominators common. This process makes the simplification process easier.

Least Common Multiple (LCM) is a method to find the smallest common multiple between any two or more numbers. A common multiple is a number which is a multiple of two or more numbers.

Properties of LCM

Properties	Description
Associative property	LCM (a, b) = LCM (b, a)
Commutative property	LCM (a, b, c) = LCM (LCM(a, b), c) = LCM(a, LCM(b, c))
Distributive property	LCM (da, db, dc) = d LCM (a, b, c)

LCM Formula

Let a and b are two given integers. The formula to find the LCM of a & b is given by:

LCM (a, b) = (a x b)/GCD (a, b)

Where GCD (a, b) means Greatest Common Divisor or Highest Common Factor of a & b.

LCM Formula for Fractions

The formula to find the LCM of fractions is given by:

L.C.M. = L.C.M Of Numerator/H.C.F Of Denominator

Different Methods of LCM

There are three important methods by which we can find the LCM of two or more numbers. They are:

Listing the Multiples

Prime Factorization Method

Division Method

Listing the Multiples: The method to find the least common multiple of any given numbers is first to list down the multiples of specific numbers and then find the first common multiple between them.

Suppose there are two numbers 11 and 33. Then by listing the multiples of 11 and 33, we get;

Multiples of 11 = 11, 22, 33, 44, 55, ….

Multiples of 33 = 33, 66, 99, ….

We can see, the first common multiple or the least common multiple of both the numbers is 33. Hence, the LCM (11, 33) = 33.

LCM By Prime Factorization: Another method to find the LCM of the given numbers is prime factorization. Suppose there are three numbers 12, 16 and 24. Let us write the prime factors of all three numbers individually.

12 = 2 x 2 x 3

16 = 2 x 2 x 2 x 2

24 = 2 x 2 x 2 x 3

Now writing the prime factors of all the three numbers together, we get;

12 x 16 x 24 = 2 x 2 x 3 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3

Now pairing the common prime factors we get the LCM. Hence, there are four 2’s and one 3. So the LCM of 12, 16 and 24 will be;

LCM (12, 16, 24) = 2 x 2 x 2 x 2 x 3 = 48

LCM By Division Method

• Finding LCM of two numbers by division method is an easy method. Below are the steps to find the LCM by division method:

• First, write the numbers, separated by commas

• Now divide the numbers, by the smallest prime number.

• If any number is not divisible, then write down that number and proceed further

• Keep on dividing the row of numbers by prime numbers, unless we get the results as 1 in the complete row

• Now LCM of the numbers will be equal to the product of all the prime numbers we obtained in the division method

Example: To find the Least Common Multiple (L.C.M) of 36 and 56,

36 = 2 × 2 × 3 × 3

56 = 2 × 2 × 2 × 7

The common prime factors are 2 × 2

The uncommon prime factors are 3 × 3 for 36 and 2 × 7 for 56.

LCM of 36 and 56 = 2 × 2 × 3 × 3 × 2 × 7 which is 504

Method of Finding HCF

H.C.F can be found using two methods – Prime factorisation and Euclid’s division algorithm.

Prime Factorisation: Given two numbers, we express both of them as products of their respective prime factors. Then, we select the prime factors that are common to both the numbers

Example – To find the H.C.F of 20 and 24

20 = 2 × 2 × 5 and 24 = 2 × 2 × 2 × 3

The factor common to 20 and 24 is 2 × 2, which is 4, which in turn is the H.C.F of 20 and 24.

Euclid’s Division Algorithm: It is the repeated use of Euclid’s division lemma to find the H.C.F of two numbers.

Example: To find the HCF of 18 and 30

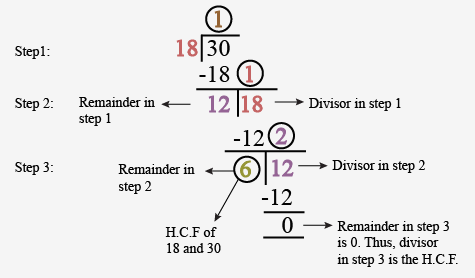
HCF by Shortcut method

Steps to find the HCF of any given numbers.

Step 1: Divide larger number by smaller number first, such as;

Larger Number/Smaller Number

Step 2: Divide the divisor of step 1 by the remainder left.

Divisor of step 1/Remainder

Step 3: Again divide the divisor of step 2 by the remainder.

Divisor of step 2/Remainder

Step 4: Repeat the process until the remainder is zero.

Step 5: The divisor of the last step is the HCF.

Important Questions

Multiple Choice questions-

1. HCF of 8, 9, 25 is

(a) 8

(b) 9

(d) 1

2. Which of the following is not irrational?

(a) ${(2 - \sqrt{3})}^{2}$

(b) ${(\sqrt{2} + \sqrt{3})}^{2}$

(d) $\frac{2 \sqrt{7}}{7}$

3. The product of a rational and irrational number is

(a) rational

(b) irrational

(d) none of above

4. The sum of a rational and irrational number is

(a) rational

(b) irrational

(d) none of above

5. The product of two different irrational numbers is always

(a) rational

(b) irrational

(d) none of above

6. The sum of two irrational numbers is always

(a) irrational

(b) rational

(d) one

7. If b = 3, then any integer can be expressed as a =

(a) 3q, 3q+ 1, 3q + 2

(b) 3q

(d) 3q+ 1

8. The product of three consecutive positive integers is divisible by

(a) 4

(b) 6

(d) only 1

9. The set A = {0,1, 2, 3, 4, …} represents the set of

(a) whole numbers

(b) integers

(d) even numbers

10. Which number is divisible by 11?

(a) 1516

(b) 1452

(d) 1121

Very Short Questions:

1.What is the HCF of the smallest composite number and the smallest prime number?

2.The decimal representation of

\frac{6}{1250}

will terminate after how many places of decimal?

3.If HCF of a and b is 12 and product of these numbers is 1800. Then what is LCM of these numbers?

4.What is the HCF of 3³ × 5 and 3² × 5²?

5.if a is an odd number, b is not divisible by 3 and LCM of a and b is P, what is the LCM of 3a and 2b?

6.If P is prime number then, what is the LCM of P, P², P³?

7.Two positive integers p and q can be expressed as p = ab² and q = a²b, a and b are prime numbers. What is the LCM of p and q?

8.A number N when divided by 14 gives the remainder 5. What is the remainder when the same number is divided by 7?

9.Examine whether

\frac{17}{30}

is a terminating decimal or not.

10.What are the possible values of remainder r, when a positive integer a is divided by 3?

11.A rational number in its decimal expansion is 1.7351. What can you say about the prime factors of q when this number is expressed in the form

\frac{p}{q}

? Give reason.

12.Without actually performing the long division, find

\frac{987}{10500}

will have terminating or non. terminating repeating decimal expansion. Give reason for your answer.

Short Questions :

1.Can the number 4ⁿ, n be a natural number, end with the digit 0? Give reason.

2.Write whether the square of any positive integer can be of the form 3m + 2, where m is a natural number. Justify your answer.

3.Can two numbers have 18 as their HCF and 380 as their LCM? Give reason.

4.An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?

5.Find the LCM and HCF of 12, 15 and 21 by applying the prime factorisation method.

6.Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.

(1) 26 and 91 (ii) 198 and 144

7.There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start from the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?

8.Write down the decimal expansiwns of the following numbers:

(i) $\frac{35}{50}$ (ii) $\frac{15}{1600}$

9.Express the number

- 0.3178

in the form of rational number

\frac{a}{b}

10.If n is an odd positive integer, show that (n² – 1) is divisible by 8.

11.The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one number is 280, then find the other number.

12.Find the value of x, y and z in the given factor tree. Can the value of ‘x’ be found without finding the value of ‘y’ and ‘z’? If yes, explain.

Real Numbers Class 10 Extra Questions Maths Chapter 1 with Solutions Answers 8

13.Show that any positive odd integer is of the form 6q + 1 or 6q + S or 6q + 5 where q is some integer.

14.The decimal expansions of some real numbers are given below. In each case, decide whether they are rational or not. If they are rational, write it in the form

\frac{p}{q}

. What can you say about the prime factors of q?

(i) 0.140140014000140000… (ii) $- 0.16$

Long Questions :

1.Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

2.Show that one and only one out of n, n + 2, n + 4 is divisible by 3, where n is any positive integer.

3.Use Euclid’s division algorithm to find the HCF of:

(i) 960 and 432

(ii) 4052 and 12576.

4.Using prime factorisation method, find the HCF and LCM of 30, 72 and 432. Also show that HCF × LCM ≠ Product of the three numbers.

5.Prove that √7 is an irrational number.

6.Show that 5 – √3 is an irrational number.

7.Using Euclid’s division algorithm, find whether the pair of numbers 847,2160 are co-prime or not.

8.Check whether 6ⁿ can end with the digit O for any natural number n.

9.Show that there is iw positive integer n for which

\sqrt{n - 1} + \sqrt{n + 1}

is rational.

10.Find the largest positive integer that will divide 398, 436 and 542 leaving remainders 7, 11 and 15 respectively.

Case Study Questions:

1.Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions at the end of his project as listed below. Answer them.

i.For what value of n, 4n ends in 0?

a.10

b.When n is even.

c.When n is odd.

d.No value of n.

ii.If a is a positive rational number and n is a positive integer greater than I, then for what value of n, 4n is a rational number?

a.When n is any even integer.

b.When n is any odd integer.

c.For all n > 1.

d.Only when n = 0.

iii.If x and y are two odd positive integers, then which of the following is true?

a.x² + y² is even.

b.x² + y² is not divisible by 4.

c.x² + y² is odd.

d.Both (a) and (b).

iv.The statement ‘One of every three consecutive positive integers is divisible by 3’ is:

a.Always true.

b.Always false.

c.Sometimes true.

d.None of these.

v.If n is any odd integer, then n2 – 1 is divisible by:

a.22

b.55

c.88

d.8

2.Real numbers are extremely useful in everyday life. That is probably one of the main reasons we all learn how to count and add and subtract from a very young age. Real numbers help us to count and to measure out quantities of different items in various fields like retail, buying, catering, publishing etc. Every normal person uses real numbers in his daily life. After knowing the importance of real numbers, try and improve your knowledge about them by answering the following questions on real life based situations.

i.Three people go for a morning walk together from the same place. Their steps measure 80cm, 85cm and 90cm respectively. What is the minimum distance travelled when they meet at first time after starting the walk assuming that their walking speed is same?

a.6120cm

b.12240cm

c.4080cm

d.None of these

ii.ln a school Independence Day parade, a group of 594 students need to march behind a band of 189 members. The two groups have to march in the same number of columns. What is the maximum number of columns in which they can march?

a.9

b.6

c.27

d.29

iii.Two tankers contain 768 litres and 420 litres of fuel respectively. Find the maximum capacity of the container which can measure the fuel of either tanker exactly.

a.4 litres

b.7 litres

c.12 litres

d.18 litres

iv.The dimensions of a room are 8m, 25cm, 6m, 75cm and 4m, 50cm. Find the length of the largest measuring rod which can measure the dimensions of room exactly.

a.1m, 25cm

b.75cm

c.90cm

d.1m, 35cm

v.Pens are sold in pack of 8 and notepads are sold in pack of 12. Find the least number of pack of each type that one should buy so that there are equal number of pens and notepads.

a.3 and 2

b.2 and 5

c.3 and 4

d.4 and 5

Assertion Reason Questions-

1.Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

(a)Both A and R are true and R is the correct explanation of A.

(b)Both A and R are true and R is not the correct explanation of A.

(c)A is true but R is false.

(d)A is false but R is true.

Assertion: 11 × 4 × 3 × 2 + 4 is a composite number.

Reason: Every composite number can be expressed as product of primes.

2.Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

(a)Both A and R are true and R is the correct explanation of A.

(b)Both A and R are true and R is not the correct explanation of A.

(c)A is true but R is false.

(d)A is false but R is true.

Assertion: If LCM = 350, product of two numbers is 25 × 70, then their HCF = 5
Reason: LCM × product of numbers = HCF

Pages: 1 2

Leave a Reply Cancel reply

Related Stories

Constructions

Probability

Statistics

You may have missed

বিজ্ঞানের জয়যাত্রা ও মানুষের ভবিষ্যৎ-Bigyaner jayayatra o manuser bhabisyat

বাংলার ঋতুচক্র-Banglar Rituchakra

প্রিয় গ্রন্থকার -“মানিক বন্দ্যোপাধ্যায়”-Priya granthakar- Manik bandyopadhay

তোমার প্রিয় কবি (জীবনানন্দ দাস )-Tomar priya kabi (Jibanananda das)