
Quadratic-Equations
Answer Key-
Multiple Choice questions-
Very Short Answer :
⇒ 42 – 4 x 2 (-7)
⇒ 16 + 56 = 72 > 0
Hence, roots of quadratic equation are real and unequal.
∴ It must satisfy the quadratic equation.
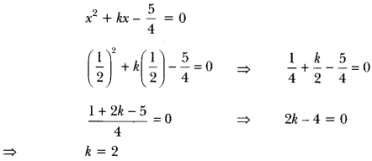
i.e., b2 – 4ac = 0
⇒ b2 = 4 ac
⇒ c =b24a
Product of the roots = ab = BA = – b
= a + b = – a and ab = -b
⇒ 2a = -b and a = -1
⇒ b = 2 and a = -1
⇒ LHS = 3x2 + 13x + 14
⇒ 3(-2)2 + 13(-2) + 14
⇒ 12 – 26 + 14 = 0
⇒ RHS Hence, x = -2 is a solution.
⇒ 64 – 64 = 0
⇒ x2 – x – 2 + x = 0
⇒ x2 – 2 = 0
D = b2 – 4ac
⇒ (-4(1)(-2) = 8 > 0
∴ Given equation has two distinct real roots.
∴ x2 – 0.9 = (0.3)2 – 0.9 = 0.09 – 0.9 ≠ 0
Hence, 0.3 is not a root of given equation.
⇒ 2(3)2 + 3 + k = 0
⇒ 18 + 3 + k = 0
⇒ k = – 21
D = 0
⇒ b2 – 4ac = 0
⇒ (- 3k)2 – 4 × 9 × k = 0
⇒ 9k2 = 36k
⇒ k = 4
Short Answer :
= √2x2 + 5x + 2x + 5√2 = 0
x(√2x + 5) + √2 (√2x + 5) = 0
= (√2x + 5)(x + √2) = 0
∴ Either √2x + 5 = 0 or x + √2 = 0
∴ x = – 5√2 or x = –√2
Hence, the roots are – 5√2 and -√2.
(ii) We have, 2x2 – x + 18 = 0
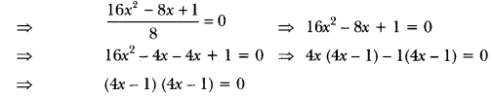
![]()
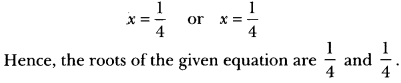
On dividing both sides by 2, we have

(ii) We have, 4x2 + 4√3x + 3 = 0
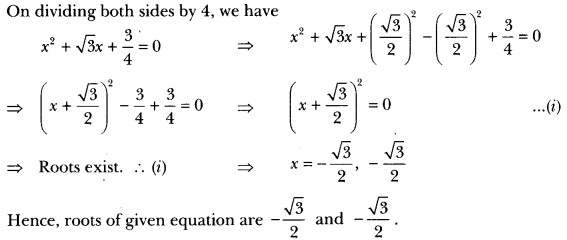
Here, a = 2, b = -7 and c = 3
Therefore, D = b+ – 4ac
⇒ D = (-7)2 – 4 × 2 × 3 = 49 – 24 = 25
∵ D > 0, ∴ roots exist.
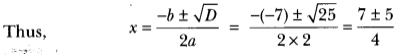

So, the roots of given equation are 3 and 12.
(ii) We have, 4x2 + 4√3x + 3 = 0
Here, a = 4, b = 4√3 and c = 3
Therefore, D = b2 – 4ac = (4√3)2 – 4 × 4 × 3 = 48 – 48 = 0
∴ D = 0, roots exist and are equal.
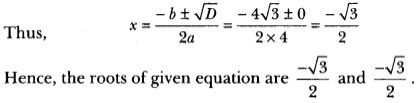
Comparing this equation with ax2 + bx + c = 0, we have
a = p2, b = p2 – q2 and c = – q2
∴ D = b2 – 4ac
⇒ (p2 – q)2 – 4 × p2 × (-q2)
⇒ (p2 – q2)2 + 4p2q2
⇒ (p2 + q3)2 > 0
So, the given equation has real roots given by
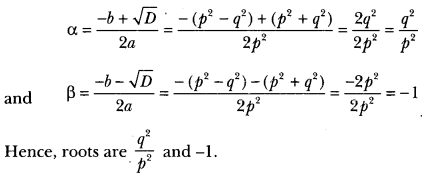
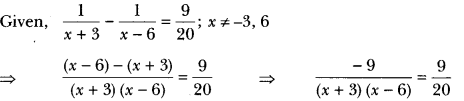
⇒ (x + 3) (x – 6)
⇒ -20 or x2 – 3x + 2 = 0
⇒ x2 – 2x -x + 2 = 0
⇒ x(x – 2) -1(x – 2) = 0)
⇒ (x – 1) (x – 2) = 0
⇒ x = 1 or x = 2
Both x = 1 and x = 2 are satisfying the given equation. Hence, x = 1, 2 are the solutions of the equation.
Here, a = 3, b = – 4√3 and c = 4
Therefore,
D = b2 – 4ac
⇒ (- 4√3)2 – 4 × 3 × 4
⇒ 48 – 48 = 0
Hence, the given quadratic equation has real and equal roots.
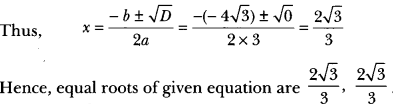
(ii) We have, 2x2 – 6x + 3 = 0
Here, a = 2, b = -6, c = 3
Therefore, D = b2 – 4ac
= (-6)2 4 × 2 × 3 = 36 – 24 = 12 > 0
Hence, given quadratic equation has real and distinct roots.
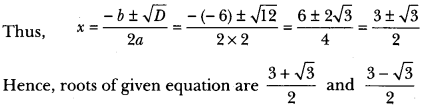
Here, a = 2, b = k, c = 3
D = b2 – 4ac = k2 – 4 × 2 × 3 = k2 – 24 For equal roots
D = 0
i.e., k2 – 24 = 0
⇒ ķ2 = 24
⇒ k = ± √24
⇒ k = + 2√6
(ii) We have, kx(x – 2) + 6 = 0
⇒ kx2 – 2kx + 6 = 0
Here, a = k, b = – 2k, c = 6
For equal roots, we have
D = 0
i.e., b2 – 4ac = 0
⇒ (-2k)2 – 4 × k × 6 = 0
⇒ 4k2 – 24k = 0
⇒ 4k (k – 6) = 0
Either 4k = 0 or k – 6 = 0
⇒ k = 0 or k = 6
But k = 0 6) because if k = 0 then given equation will not be a quadratic equation).
So, k = 6.
D = (b – c)2 – 4(a – b) (c – a) = 0
⇒ b2 + c2 – 2bc – 4(ac – a2 – bc + ab)
⇒ b2 + c2 – 2bc – 4ac + 4a2 + 4bc – 4ab = 0
⇒ 4a2 + b2 + c2 – 4ab + 2bc – 4ac = 0
⇒ (2a)2 + (- b)2 + (-c)2 + 2(2a) (-b) + 2(-b) (-c) + 2(-c) 2a = 0
⇒ (2a – b – c)2 = 0
⇒ 2a – b – c = 0
⇒ 2a = b + c. Hence Proved.
Here, A = 1 + m2, B = 2mc and C = c2 – a2
Since the given equation has equal roots, therefore D = 0 = B2 – 4AC = 0.
⇒ (2mc)2 – 4(1 + m2) (c2 – a2) = 0
⇒ 4m2c2 – 4(c2 – a2 + m2c2 – m2a2) = 0
⇒ m2c2 – c2 + a2 – m2c2 + m2a2 = 0. [Dividing throughout by 4]
⇒ – c2 + a2 (1 + m2) = 0
⇒ c2 = a(1 + m2) Hence Proved
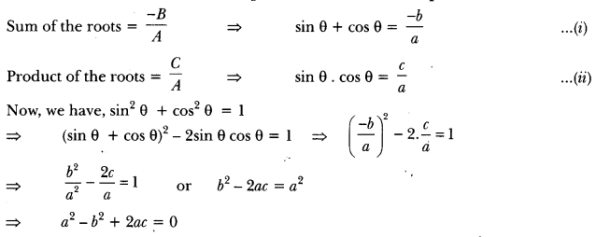
Long Answer :
Here, A = ab, B = b2 – ac, C = – bc
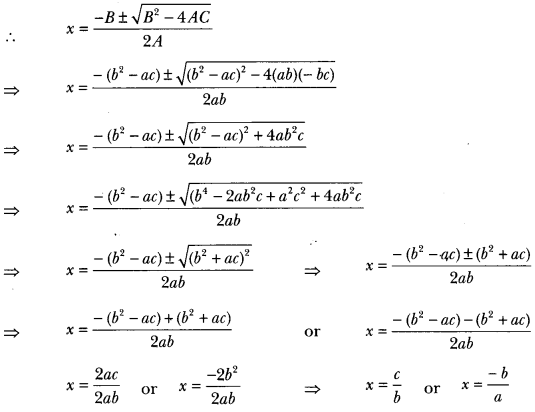
i.e., b2 – 4ac = 0
In (2p + 1 )x2 – (7p + 2)x + (7p – 3) = 0
Here, a = (2p + 1), b = -(7p + 2), c = (7p – 3)
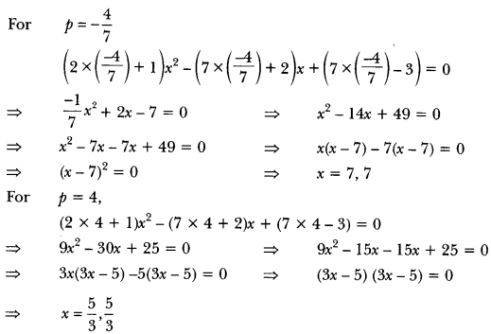
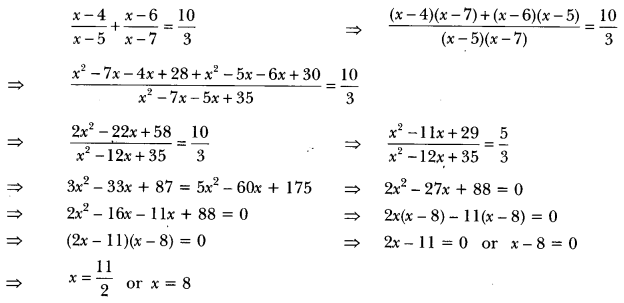
So, 3 years ago, Rehman’s age = (x – 3) years
And 5 years from now, Rehman’s age = (x + 5) years
Now, according to question, we have
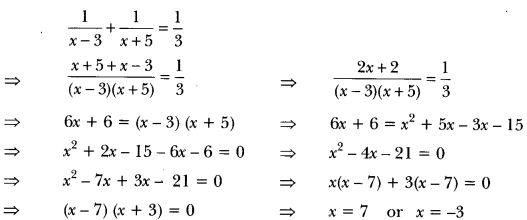
But x ≠ -3 (age cannot be negative)
Therefore, present age of Rehman = 7 years.
According to the question,
Difference of numbers, x – y = 5 ⇒ x = 5 + y …..(i)
Difference of the reciprocals,
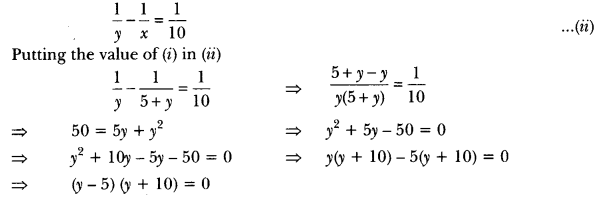
∴ y is a natural number.
∵ y = 5
Putting the value of y in (i), we have
⇒ x = 5 + 5
⇒ x = 10
The required numbers are 10 and 5.
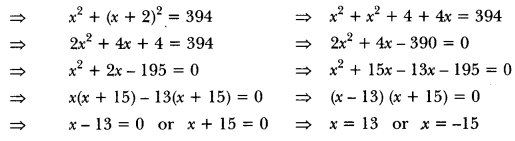
Hence, the numbers are 13 and 15 or -15 and -13.
According to given condition,
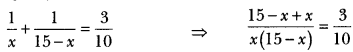
⇒ 150 = 3x(15 – x)
⇒ 50 = 15x – x2
⇒ x2 – 15x + 50 = 0
⇒ x2 – 5x – 10x + 50 = 0
⇒ x(x – 5) -10(x – 5) = 0
⇒ (x – 5)(x – 10) = 0
⇒ x = 5 or 10.
When x = 5, then 15 – x = 15 – 5 = 10
When x = 10, then 15 – x = 15 – 10 = 5
Hence, the two numbers are 5 and 10.
Therefore, Shefali’s marks in English is (30 – x).
Now, according to question,
⇒ (x + 2) (30 – x – 3) = 210
⇒ (x + 2) (27 – x) = 210
⇒ 27x – x2 + 54 – 2x = 210
⇒ 25x – x2 + 54 – 210 = 0
⇒ 25x – x2 – 156 = 0
⇒ -(x2 – 25x + 156) = 0
⇒ x2 – 25x + 156 = 0
= x2 – 13x – 12x + 156 = 0
⇒ x(x – 13) – 12(x – 13) = 0
⇒ (x – 13) (x – 12) = 0
Either x – 13 or x – 12 = 0
∴ x = 13 or x = 12
Therefore, Shefali’s marks in Mathematics = 13
Marks in English = 30 – 13 = 17
or Shefali’s marks in Mathematics = 12
marks in English = 30 – 12 = 18.

But x cannot be negative, so x ≠ – 45
therefore, x = 40
Hence, the uniform speed of train is 40 km/h
Then, x2 + y2 = 468 …(i)
Let x be the length of the side of the bigger square.
4x – 4y = 24
⇒ x – y = 6 or x = y + 6 …(ii)
Putting the value of x in terms of y from equation (ii), in equation (i), we get
(y + 6)2 + y2 = 468
⇒ y2 + 12y + 36 + y2 = 468 or 232 + 12y – 432 = 0
⇒ y2 + 6y – 216 = 0
⇒ y2 + 18y – 12y – 216 = 0
⇒ y(y + 18) – 12(y + 18) = 0
⇒ (y + 18)(y – 12) = 0
Either y + 18 = 0 or y – 12 = 0
⇒ y = -18 or y = 12
But, sides cannot be negative, so y = 12
Therefore, x = 12 + 6 = 18
Hence, sides of two squares are 18 m and 12 m.
Case Study Answers:
Solution:
⇒ x2 + 3x + 7 = 5x – 11
⇒ x2 – 2x + 18 = 0 is a quadratic equation.
⇒ x2 -2x -8 = x2 – x – 12
⇒ x – 4 = 0 is not a quadratic equation.
⇒ 2x3 + x2 – 4 = 5x2 – 10
⇒ 2x3 – 4x2 + 6 = 0 is not a quadratic equation.
x3 + 6x2 – 7x = 6x2 – 9x
x3 + 2x = 0 is not a quadratic equation.
Solution:
Let two consecutive integers be x, x + 1. Given, x2 + (x + 1)2 = 650.
⇒ 2x2 + 2x + 1 – 650 = 0
⇒ 2x2 + 2x – 649 = 0
Solution:
Let the two numbers be x and 15 – x. Given 1x+115−x=310
⇒ 10(15 – x + x) = 3x(15 – x)
⇒ 50 = 15x – x2
⇒ x2 -15x + 50 = 0
Solution:
Let the numbers be x and x + 3. Given, x(x + 3) = 504
⇒ x2 + 3x – 504 = 0
Solution:
Let the number be x. According to question, x2 – 84 = 3(x + 8)
⇒ x2 – 84 = 3x + 24
⇒ x2 – 3x – 108 = 0
Solution:
Let the number be x .Accoding to question x+12=160xx+12=160x
⇒ x2 + 12x – 160 = 0
Assertion Reason Answer-






