
Probability
Probability
In this chapter, the term experiment will stand for random experiment.
Number of outcomes favourable to E Number of all possible outcomes of the experiment
If P(A) > P(B) then event A is more likely to occur than event B.
If P(A) = P(B) then events A and B are equally likely to occur.
 A pack of playing cards consist of 52 cards which are divided into 4 suits of 13 cards each. Each suit consists of one ace, one king, one queen, one jack and 9 other cards numbered from 2 to 10. Four suits are named as spades, hearts, diamonds and clubs.
A pack of playing cards consist of 52 cards which are divided into 4 suits of 13 cards each. Each suit consists of one ace, one king, one queen, one jack and 9 other cards numbered from 2 to 10. Four suits are named as spades, hearts, diamonds and clubs.
 King, queen and jack are face cards.
King, queen and jack are face cards.
The formula for finding the geometric probability of an event is given by:
P(E)=Measure of the specified part of the regionMeasure of the whole region
Here, ‘measure’ may denote length, area or volume of the region or space.
Event and outcome
An Outcome is a result of a random experiment. For example, when we roll a dice getting six is an outcome.
An Event is a set of outcomes. For example when we roll dice the probability of getting a number less than five is an event.
Note: An Event can have a single outcome
Events and Types of Events in Probability
What are Events in Probability?
A probability event can be defined as a set of outcomes of an experiment. In other words, an event in probability is the subset of the respective sample space. So, what is sample space?
The entire possible set of outcomes of a random experiment is the sample space or the individual space of that experiment. The likelihood of occurrence of an event is known as probability. The probability of occurrence of any event lies between 0 and 1.
The sample space for the tossing of three coins simultaneously is given by:
S = {(T , T , T) , (T , T , H) , (T , H , T) , (T , H , H ) , (H , T , T ) , (H , T , H) , (H , H, T) ,(H , H , H)}
Suppose, if we want to find only the outcomes which have at least two heads; then the set of all such possibilities can be given as:
E = { (H , T , H) , (H , H ,T) , (H , H ,H) , (T , H , H)}
Thus, an event is a subset of the sample space, i.e., E is a subset of S.
There could be a lot of events associated with a given sample space. For any event to occur, the outcome of the experiment must be an element of the set of event E.
What is the Probability of Occurrence of an Event?
The number of favourable outcomes to the total number of outcomes is defined as the probability of occurrence of any event. So, the probability that an event will occur is given as:
Types of Events in Probability:
Some of the important probability events are:
Impossible and Sure Events
If the probability of occurrence of an event is 0, such an event is called an impossible event and if the probability of occurrence of an event is 1, it is called a sure event. In other words, the empty set ϕ is an impossible event and the sample space S is a sure event.
Simple Events
Any event consisting of a single point of the sample space is known as a simple event in probability. For example, if S = {56, 78 , 96 , 54 , 89} and E = {78} then E is a simple event.
Compound Events
Contrary to the simple event, if any event consists of more than one single point of the sample space then such an event is called a compound event. Considering the same example again, if S = {56 ,78 ,96 ,54 ,89}, E1 = {56 ,54 }, E2 = {78 ,56 ,89 } then, E1 and E2 represent two compound events.
Independent Events and Dependent Events
If the occurrence of any event is completely unaffected by the occurrence of any other event, such events are known as an independent event in probability and the events which are affected by other events are known as dependent events.
Mutually Exclusive Events
If the occurrence of one event excludes the occurrence of another event, such events are mutually exclusive events i.e. two events don’t have any common point. For example, if S = {1, 2 , 3 , 4 , 5 , 6} and E1, E2 are two events such that E1 consists of numbers less than 3 and E2 consists of numbers greater than 4.
So, E1 = {1,2} and E2 = {5,6} .
Then, E1 and E2 are mutually exclusive.
Exhaustive Events
A set of events is called exhaustive if all the events together consume the entire sample space.
Complementary Events
For any event E1 there exists another event E1‘ which represents the remaining elements of the sample space S.
E1 = S − E1‘
If a dice is rolled then the sample space S is given as S = {1 , 2 , 3 , 4 , 5 , 6 }. If event E1 represents all the outcomes which is greater than 4, then E1 = {5, 6} and E1‘ = {1, 2, 3, 4}.
Thus E1‘ is the complement of the event E1.
Similarly, the complement of E1, E2, E3……….En will be represented as E1‘, E2‘, E3‘……….En‘
Experimental Probability
Experimental probability can be applied to any event associated with an experiment that is repeated a large number of times.
A trial is when the experiment is performed once. It is also known as empirical probability.
Experimental or empirical probability: P(E) =Number of trials where the event occurred/Total Number of Trials
You and your 3 friends are playing a board game. It’s your turn to roll the die and to win the game you need a 5 on the dice. Now, is it possible that upon rolling the die you will get an exact 5? No, it is a matter of chance. We face multiple situations in real life where we have to take a chance or risk. Based on certain conditions, the chance of occurrence of a certain event can be easily predicted. In our day to day life, we are more familiar with the word ‘chance and probability’. In simple words, the chance of occurrence of a particular event is what we study in probability. In this article, we are going to discuss one of the types of probability called “Experimental Probability” in detail.
Theoretical Probability
Theoretical Probability, P(E) = Number of Outcomes Favourable to E / Number of all possible outcomes of the experiment
Here we assume that the outcomes of the experiment are equally likely.
Every one of us would have encountered multiple situations in life where we had to take a chance or risk. Depending on the situation, it can be predicted up to a certain extent if a particular event is going to take place or not. This chance of occurrence of a particular event is what we study in probability. In our everyday life, we are more accustomed to the word ‘chance’ as compared to the word ‘probability’. Since Mathematics is all about quantifying things, the theory of probability basically quantifies these chances of occurrence or non-occurrence of certain events. In this article, we are going to discuss what is probability and its two different types of approaches with examples.
In Mathematics, the probability is a branch that deals with the likelihood of the occurrences of the given event. The probability value is expressed between the range of numbers from 0 to 1. The three basic rules connected with the probability are addition, multiplication, and complement rules.
Theoretical Probability Vs Experimental Probability
Probability theory can be studied using two different approaches:
Theoretical Probability
Experimental Probability
Theoretical Probability Definition
Theoretical probability is the theory behind probability. To find the probability of an event using theoretical probability, it is not required to conduct an experiment. Instead of that, we should know about the situation to find the probability of an event occurring. The theoretical probability is defined as the ratio of the number of favourable outcomes to the number of possible outcomes.
Probability of Event P(E) = No. of. Favourable outcomes/ No. of. Possible outcomes.
Experimental Probability Definition
The experimental probability also is known as an empirical probability, is an approach that relies upon actual experiments and adequate recordings of occurrence of certain events while the theoretical probability attempts to predict what will happen based upon the total number of outcomes possible. The experimental Probability is defined as the ratio of the number of times that event occurs to the total number of trials.
Probability of Event P(E) = No. of. times that event occurs/ Total number of trials
The basic difference between these two approaches is that in the experimental approach; the probability of an event is based on what has actually happened by conducting a series of actual experiments, while in theoretical approach; we attempt to predict what will occur without actually performing the experiments.
Elementary Event
An event having only one outcome of the experiment is called an elementary event.
Example: Take the experiment of tossing a coin n number of times. One trial of this experiment has two possible outcomes: Heads(H) or Tails(T). So for an individual toss, it has only one outcome, i.e Heads or Tails.
Sum of Probabilities
The sum of the probabilities of all the elementary events of an experiment is one.
Example: take the coin-tossing experiment. P(Heads) + P(Tails)
= (1/2)+ (1/2) =1
Impossible event
An event that has no chance of occurring is called an Impossible event, i.e. P(E) = 0.
E.g: Probability of getting a 7 on a roll of a die is 0. As 7 can never be an outcome of this trial.
Sure event
An event that has a 100% probability of occurrence is called a sure event. The probability of occurrence of a sure event is one.
E.g: What is the probability that a number obtained after throwing a die is less than 7?
So, P(E) = P(Getting a number less than 7) = 6/6= 1
Range of Probability of an event
The range of probability of an event lies between 0 and 1 inclusive of 0 and 1, i.e. 0≤P(E)≤1.
Geometric Probability
Geometric probability is the calculation of the likelihood that one will hit a particular area of a figure. It is calculated by dividing the desired area by the total area. In the case of Geometrical probability, there are infinite outcomes.
Complementary Events
Complementary events are two outcomes of an event that are the only two possible outcomes. This is like flipping a coin and getting heads or tails.
P(E)+P(¯¯¯¯E)=1, where E and ¯¯¯¯E
are complementary events. The event ¯¯¯¯E, representing ‘not E‘, is called the complement of the event E.
For any event A, there exists another event A‘ which shows the remaining elements of the sample space S. A’ denotes complementary event of A.
A’ = S – A.
Event A and A’ are mutually exclusive and exhaustive.
Consider the example of tossing a coin. Let P(E) denote the probability of getting a tail when a coin is tossed. Then probability of getting a head is denoted by
P(¯¯¯¯E). P(E)+P(¯¯¯¯E)=1
The event P(¯¯¯¯E) means ‘Not E’.
Example 1:
A bag contains only lemon-flavoured candies. Arjun takes out one candy without looking into the bag. What is the probability that he takes out an orange-flavoured candy?
Solution:
Let us take the number of candies in the bag to be 100.
Number of orange flavoured candies = 0 [since the bag contains only lemon-flavoured candies]
Hence, the probability that he takes out an orange-flavoured candy is:
P (Taking orange-flavoured candy) = Number of orange flavoured candies / Total number of candies.
= 0/100 = 0
Hence, the probability that Arjun takes out an orange-flavoured candy is 0.
This proves that the probability of an impossible event is 0.
Example 2:
A game of chance consists of spinning an arrow that comes to rest pointing at any one of the numbers such as 1, 2, 3, 4, 5, 6, 7, 8 and these are equally likely outcomes. What is the probability that it will point at (i)8, (ii) Number greater than 2 (iii) Odd numbers.
Solution:
Sample Space = {1, 2, 3, 4, 5, 6, 7, 8}
Total Numbers = 8
(i) Probability that the arrow will point at 8:
Number of times we can get 8 = 1
P (Getting 8) = 1/8.
(ii) Probability that the arrow will point at the number greater than 2:
Number greater than 2 = 3, 4, 5, 6, 7, 8.
No. of numbers greater than 2 = 6
P (Getting numbers greater than 2) = 6/8 = 3/4.
(iii) Probability that the arrow will point at the odd numbers:
Odd number of outcomes = 1, 3, 5, 7
Number of odd numbers = 4.
P (Getting odd numbers) = 4/8 = ½.
PROBABILITY
Multiple Choice questions-
1. An event is very unlikely to happen. Its probability is closest to:
(a) 0.0001
(b) 0.001
(c) 0.01
(d) 0.1
2. If the probability of an event is P, the probability of its complementary event will be:
(a) P – 1
(b) P
(c) 1 – p
(d) 1 –1p
3. If P(A) denotes the probability of an event then:
(a) P(A) < 0
(b) P(A) > 0
(c) 0 ≤ P(A) ≤ 1
(d) -1 ≤ P(A) ≤ 0
4. A card is drawn from a deck of 52 cards. The event E is that card is not an ace of hearts. The number of outcomes favourable to E is:
(a) 4
(b) 13
(c) 48
(d) 51
5. The probability of getting a bad egg in a lot of 400 is 0.035. The number of bad eggs in the lot is:
(a) 7
(b) 14
(c) 21
(d) 28
6. A girl calculate that the probability of her winning the first prize in a lottery is 0.08. If 6000 tickets are sold, how many tickets has she bought?
(a) 40
(b) 240
(c) 480
(d) 750
7. One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number which is a multiple of 5 is:
![]()
8. Someone is asked to take a number from 1 to 100. The probability that it is a prime is:
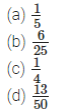
9. A school has five houses A, B, C, D and E. A class has 23 students, 4 from house A, 8 from house B, 5 from house C, 2 from house D and rest from house E. A single student is selected at random to be the class monitor. The probability that the selected student is not from A, B and C is:
(a) 423
(b) 623
(c) 823
(d) 1723
10. When a die is thrown, the probability of getting an odd number less them 3 is:
(a) 16
(b) 13
(c) 12
(d) 0
Very Short Questions:
Short Questions :
![]()
The die is thrown once. What is the probability of getting (i) A? (ii) D?
(i) all heads.
(ii) exactly two heads.
(iii) exactly one head.
(iv) at least two heads.
(v) at least two tails
(i) a prime number.
(ii) a number lying between 2 and 6.
(iii) an odd number
(i) What is the probability of getting a number greater than 4?
(ii) What is the probability of getting a number less than or equal to 4?
Long Questions :
(i) a king of red colour.
(ii) a face card.
(iii) a red face card.
(iv) the jack of hearts.
(v) a spade.
(vi) the queen of diamonds.
(i) an ace.
(ii) red.
(iii) either red or king.
(iv) red and a king.
(v) a face card.
(vi) a red face card.
(vii) “2′ of spades.
(viii) ’10’ of a black suit.
(i) an odd number.
(ii) a multiple of 5.
(iii) a perfect square.
(iv) an even prime number.
Case Study Questions:
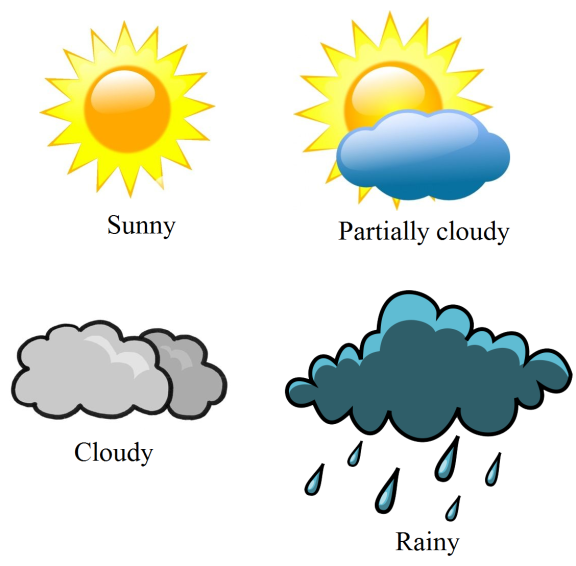
![]()
lf the forecast is 100% correct for June, then answer the following questions.
![]()
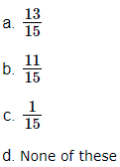



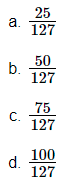
Assertion Reason Questions-
Assertion: The probability of winning a game is 0.4, then the probability of losing it, is 0.6.
Reason: P (E) + P(not E) = 1
Assertion: If the probability of an event is P, then probability of its complementary event will be 1 × P.
Reason: LCM × product of numbers = HCF
Answer Key-
Multiple Choice questions-
Very Short Answer :

False, because the outcome 3 is more likely than the other numbers.
(exactly one head) =24=12
∴ P (black queen) =252=126
P (E) + P (not E) = 1
P (not E) = 1 – P (E) = 1 – 0.05 = 0.95
∴ P (no head) =14
Favourable outcomes are {(1,3), (3, 1), (2, 2), (3, 6), (6,3), (4, 5), (5, 4)}
∴ Required probability =736
∴ P (Prime number) =25100 = 14
Short Answer :
The possible ways are, (1, 2), (2, 1), (1, 3), (3, 1), (5, 1), (1, 5)
So, number of possible ways = 6
∴ Required probability =636=16
∴ Non-prime numbers from 1 to 25 = 25 – 9 = 16.
⇒ P (non-prime number) =1625
∴ P (an ace and black card) =252=126
Then, the number of outcomes favourable to the event E = 44 (4 kings and 4 aces are not there)
∴ P(E)=4452 =1113
(ii) As the bag contains only lemon flavoured candies. So, the event related to the experiment of taking out lemon flavoured candies is certain event. So, its probability is 1.
∴ Total number of elementary outcomes = 144
Now, favourable number of elementary events = 132
∴ Probability that a pen taken out is good one =132144 =1112
The probability of Sangeeta’s winning = P(S) = 0.62
As the events R and S are complementary
∴ The probability of Reshma’s winning = P(R) = 1 – P(S)
= 1 – 0.62 = 0.38.
(i) Let E be the event of getting a letter A.
∴ Favourable number of elementary events = 2
∴ P(E) =26=13
(ii) Let E be the event of getting a letter D.
∴ Favourable number of elementary events = 1
∴ P(E) = 16
The number of outcomes favourable to the event E = 24 (26 red cards and 2 black kings are not there, so 52 – 28 = 24)
∴ P(E)=2452=1613
Total number of defective bulbs in the box = 15
Total number of non-defective bulbs in the box = 400 – 15 = 385
![]()
The outcomes favourable to the event E, ‘at least one head’ are (H, H), (H, T) and (T, H). So, the number of outcomes favourable to E is 3.
Therefore, P(E) =34
i.e., the probability that Harpreet gets at least one head is 34.
HHH, HHT, HTH, THH, TTH, THT, HTT, TTT
∴ Total number of possible outcomes = 8
Now, Ramesh will lose the game if he gets
HHT, HTH, THH, TTH, THT, HTT
∴ Favourable number of events = 6
∴ Probability that he lose the game =68=34
HHH, HHT, HTH, THH, HTT, THT, TTH, TTT
∴ Total number of elementary events = 8
(i) The event “getting all heads” is said to occur, if the elementary event HHH occurs, i.e., HHH is an outcome.
∴ Favourable number of elementary events = 1
Hence, required probability =18
(ii) The event “getting two heads” will occur, if one of the elementary events HHT, THH, HTH occurs.
∴ Favourable number of elementary events = 3
Hence, required probability =38
(iii) The event of “getting one head”, when three coins are tossed together, occurs if one of the elementary events HTT, THT, TTH, occurs.
Favourable number of elementary events = 3
Hence, required probability =38
(iv) If any of the elementary events HHH, HHT, HTH, and THH is an outcome, then we say that
the event “getting at least two heads” occurs.
∴ Favourable number of elementary events = 4
honom 4 Hence, required probability =48=12
(v) Similar as (iv) P (getting at least two tails) =48=12
(i) Let E denotes the event of getting a prime number.
So, favourable number of outcomes = 3 (i.e., 2, 3, 5)
∴ P(E) =36=12
(ii) Let E be the event of getting a number lying between 2 and 6.
∴ Favourable number of elementary events (outcomes) = 3 (i.e., 3, 4, 5)
∴ P(E) =36=12
(iii) Let E be the event of getting an odd number.
∴ Favourable number of elementary events = 3 (i.e., 1, 3, 5)
∴ P(E) =36=12
P(E) = P (number greater than 4) =26=13
(ii) Let F be the event ‘getting a number less than or equal to 4’.
Number of possible outcomes = 6
Outcomes favourable to the event F are 1, 2, 3, 4.
So, the number of outcomes favourable to F is 4.
Therefore, P(F) =46=23
Long Answer :
(i) As we know that there are two suits of red card, i.e., diamond and heart and each suit contains one king.
∴ Favourable number of outcomes = 2
∴ Probability of getting a king of red colour =252=126
(ii) As we know that kings, queens and jacks are called face cards. Therefore, there are 12 face cards.
∴ Favourable number of elementary events = 12
∴ Probability of getting a face card =1252=313
(iii) As we know there are two suits of red cards, i.e., diamond and heart and each suit contains 3 face cards.
∴ Favourable number of elementary events = 2 × 3 = 6
∴ Probability of getting red face card =652=326
(iv) Since, there is only one jack of hearts.
∴ Favourable number of elementary events = 1
∴ Probability of getting the jack of heart =152
(v) Since, there are 13 cards of spade.
∴ Favourable number of elementary events = 13
∴ Probability of getting a spade =1352=14
(vi) Since, there is only one queen of diamonds.
∴ Favourable number of outcomes (elementary events) = 1
∴ Probability of getting a queen of diamond =152
So, total number of elementary events = 52
(i) There are four ace cards in a pack of 52 cards. So, one ace can be chosen in 4 ways.
∴ Favourable number of elementary events = 4
Hence, required probability =452=113
(ii) There are 26 red cards in a pack of 52 cards. Out of 26 red cards, one card can be chosen in 26 ways.
∴ Favourable number of elementary events = 26
Hence, required probability =2652=12
(iii) There are 26 red cards, including two red kings, in a pack of 52 playing cards. Also, there are 4 kings, two red and two black. Therefore, card drawn will be a red card or a king if it is any one of 28 cards (26 red cards and 2 black kings).
∴ Favourable number of elementary events = 28
Hence, required probability =2852=713
(iv) A card drawn will be red as well as king, if it is a red king. There are 2 red kings in a pack of 52 playing cards.
∴ Favourable number of elementary events = 2
Hence, required probability =252=126
(v) In a deck of 52 cards: kings, queens, and jacks are called face cards. Thus, there are 12 face cards. So, one face card can be chosen in 12 ways.
Favourable number of elementary events = 12
Hence, required probability =1252=313
(vi) There are 6 red face cards 3 each from diamonds and hearts. Out of these 6 red face cards, one card can be chosen in 6 ways.
∴ Favourable number of elementary events = 6
Hence, required probability =652=326
(vii) There is only one ‘2’ of spades.
∴ Favourable number of elementary events = 1 Hence, required probability = 2
(viii) There are two suits of black cards viz. spades and clubs. Each suit contains one card bearing number 10.
∴ Favourable number of elementary events = 2
Hence, required probability =252=126
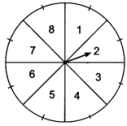
Here, total number of elementary events (possible outcomes) = 8
(i) We have only one ‘P’ on the spining plant.
∴ Favourable number of outcomes = 1
Hence, the probability that arrow points at 8 =126.
(ii) We have four odd points (i.e., 1, 3, 5 and 7)
∴ Favourable number of outcomes = 4
∴ Probability that arrow points at an odd number =48=12
(iii) We have 6 numbers greater than 2, i.e., 3, 4, 5, 6, 7 and 8.
Therefore, favourable number of outcomes = 6
∴ Probability that arrow points at a number greater than 2 =68=34
(iv) We have 8 numbers less than 9, i.e, 1, 2, 3, … 8.
∴ Favourable number of outcomes = 8
∴ Probability that arrow points at a number less than 9 =88= 1
The same is true when the blue die shows ‘2’, ‘3’, ‘4’, ‘5’ or ‘6’. The possible outcomes of the experiment are listed in the table below; the first number in each ordered pair is the number appearing on the blue die and the second number is that on the grey die. So, the number of possible outcomes = 6 × 6 = 36.
(i) The outcomes favourable to the event the sum of the two numbers is 8′ denoted by E, are :
(2, 6), (3, 5), (4, 4), (5, 3), (6, 2) (see figure)
i.e., the number of outcomes favourable to E = 5.
Hence, P(E) =536
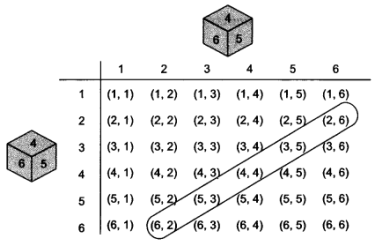
(ii) As you can see from figure, there is no outcome favourable to the event F, ‘the sum of two numbers is 13’.
So, P(F) =036= 0
(iii) As you can see from figure, all the outcomes are favourable to the event G, ‘sum of two numbers ≤ 12.
So, P(G) =3636= 1.
Total number of outcomes = 49
(i) Odd number
Favourable outcomes : 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49
Number of favourable outcomes = 25
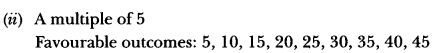


Case Study Answer-
Total number of days in June = 30

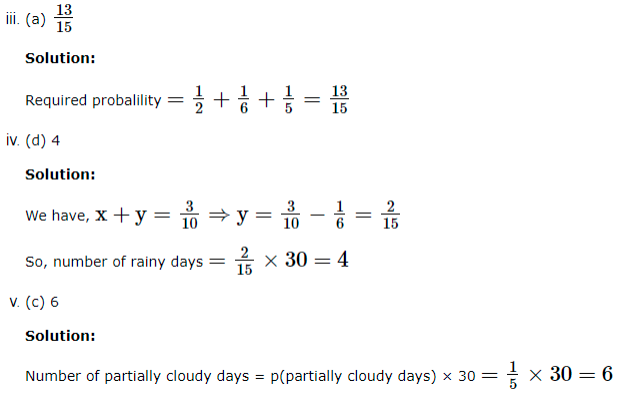
Total number of cartons in the store = 80 + 90 + 38 + 42 = 250
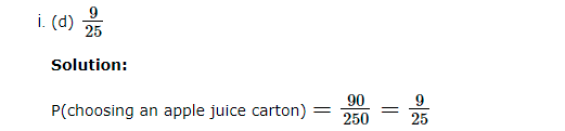
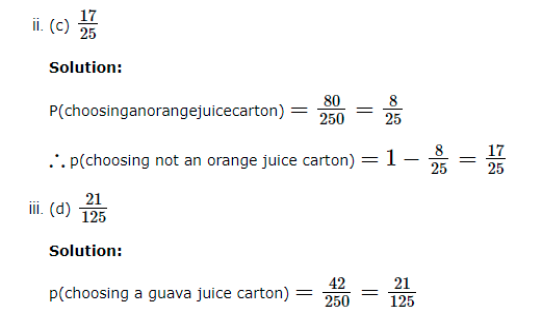

Assertion Reason Answer-





