সামান্তরিক বিষয়ক উপপাদ্য – Theorems on Parallelogram 2

উপপাদ্য 26 (Theorem 26)

.

বিবৃতি (Statement)

তিন বা ততোধিক সমান্তরাল সরলরেখা কোন ছেদক হইতে সমান সমান অংশ ছিন্ন করিলে উহারা অপর যে কোন ছেদক হইতেও সমান সমান অংশ ছিন্ন করিবে।

[If three or more parallel straight lines make equal intercepts on any transversal, they make equal intercepts on any other transversal.]

.

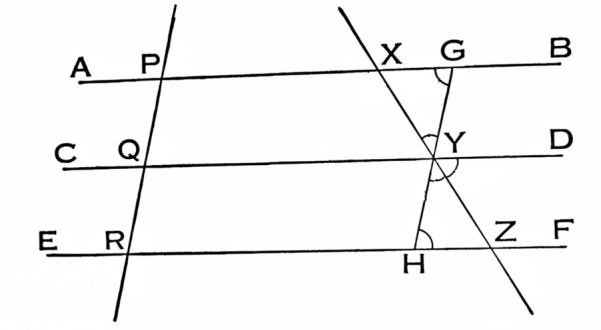
AB, CD ও EF সমান্তরাল সরলরেখা PQR ছেদক হইতে PQ ও QR দুইটি সমান অংশ ছিন্ন করিয়াছে এবং XYZ ছেদক হইতে XY ও YZ দুইটি অংশ ছিন্ন করিয়া।

.

প্রমাণ করিতে হইবে যে, XY = YZ

.

অঙ্কন। Y বিন্দু দিয়া PQR এর সমান্তরাল GYH সরলরেখা টান; উহা যেন AB ও EF এর সহিত যথাক্রমে G ও H বিন্দুতে মিলিত হইল।

.

প্রমাণ। PQYG একটি সামান্তরিক, ∴ PQ = GY

এইরূপ, QRHY একটি সামান্তরিক, ∴ QR = YH

কিন্তু PQ = QR, ∴ GY = YH

আবার, AB || EF এবং GYH উহাদের সহিত মিলিত হইয়াছে,

∴ ∠XGY = একান্তর ∠YHZ (উপ. 3)

অতএব, YXG ও YZH ত্রিভুজ দুইটির

GY = YH,

∠XGY = ∠YHZ এবং ∠XYG = বিপ্রতীপ ∠ZYH;

∴ ত্রিভুজ দুইটি সর্বসম, (স্বতঃ 6)

∴ XY = YZ

.

অনুসিদ্ধান্ত : কোন ত্রিভুজের ভূমির সহিত সমান্তরাল করিয়া অঙ্কিত কতকগুলির সরলরেখা যদি ত্রিভুজটির এক বাহুকে কতিপয় সমান অংশে বিভক্ত করে, তবে উহারা অপর বাহুটিকেও তুল্যসংখ্যক সমান অংশে বিভক্ত করিবে।

.

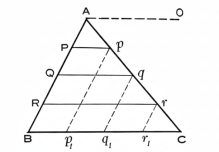
ABC ত্রিভুজের BC ভূমির সহিত সমান্তরাল করিয়া অঙ্কিত Pp, Qq ও Rr সরলরেখাগুলি AB বাহুকে সমান চারি অংশে বিভক্ত করিয়াছে।

প্রমাণ করিতে হইবে যে, উহারা AC কে p, q ও r বিন্দুগুলিতে সমান চারি অংশে বিভক্ত করিবে।

.

অঙ্কন। A বিন্দু হইতে BC-এর সমান্তরাল AO সরলরেখা টান।

.

প্রমাণ। AO, Pp, Qq, Rr ও BC সরলরেখা এবং উহারা AB-ছেদককে সমান চারি অংশে বিভক্ত করিয়াছে; অতএব উহারা AC-ছেদককেও সমান চারি অংশে বিভক্ত করে (উপ. 26)।

.

মন্তব্য। উল্লেখিত অঙ্কানুসারে Pp1, Qq1 ও Rr1 কে BC-এর আশ্রয়রূপে প্রকাশ করা যাইতে পারে।

.

P,q, ও r হইতে AB-এর সমান্তরাল করিয়া BC পর্যন্ত pp1, qq1 ও rr1 সরলরেখাগুলি টান। তাহা হইলে AC সমান চারি অংশে বিভক্ত হইয়াছে বলিয়া BC-ও সমান চারি অংশে বিভক্ত হইয়াছে।

∴ B$p_1$ = $\frac{1}{4}$ BC; B$q_1$ = $\frac{2}{4}$ BC; B$r_1$ = $\frac{3}{4}$ BC

কিন্তু PB$p_{1}p$  একটি সামান্তরিক; ∴ Pp = B$p_1$ = $\frac{1}{4}$ BC;

এইরূপ, Qq = B$q_1$ = $\frac{2}{4}$ BC; Rr = B$r_1$ = $\frac{3}{4}$ BC

এইরূপ, সমান্তরাল সরলরেখাগুলি যদি AB কে সমান n অংশে বিভক্ত করে, তবে

Pp = $\frac{1}{n}$BC; Qq = $\frac{2}{n}$BC; Rr = $\frac{3}{n}$BC; ইত্যাদি।

.

লম্ব অভিক্ষেপ

.

.

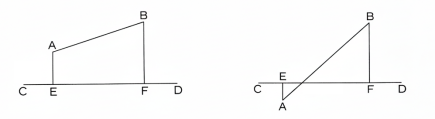
111 AB সরলরেখার A ও B প্রান্তদ্বয় হইতে CD সরলরেখার উপর AE ও BF লম্ব টানিলে EF কে CD-র উপর AB-র লম্ব অভিক্ষেপ (Orthogonal projection) বলে।

.

.

উপপাদ্য 27 (Theorem 27)

.

বিবৃতি (Statement):

ত্রিভুজের এক বাহুর মধ্যবিন্দু দিয়া অপর এক বাহুর সহিত সমান্তরাল করিয়া সরলরেখা টানিলে উহা তৃতীয় বাহুকে সমদ্বিখন্ডিত করে।

[The straight line drawn through the middle point of one side of a triangle parallel to another side bisects the

third side.]

.

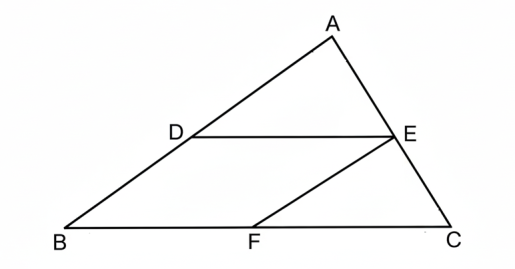
ABC ত্রিভুজের AB বাহুর D মধ্যবিন্দু। BCর সহিত সমান্তরাল করিয়া অঙ্কিত DE সরলরেখা AC কে E বিন্দুতে ছেদ করিয়াছে।

প্রমাণ করিতে হইবে যে, AE = EC

.

অঙ্কন। E দিয়া ABর সহিত সমান্তরাল করিয়া EF সরলরেখা টান। উহা যেন BCর সহিত F বিন্দুতে মিলিত হইল।

প্রমাণ। AB ও EF সমান্তরাল এবং AC উহাদের সহিত মিলিত হইয়াছে,

∴ ∠DAE = অনুরূপ ∠FEC। (উপ. 3)

আবার, DE ও BC সমান্তরাল এবং AC উহাদের সহিত মিলিত হইয়াছে,

∴ ∠AED = অনুরূপ ∠ECF। (উপ. 3)

আবার, ∴ AD = DB (কল্পনা)

                                     এবং DB = EF (সামান্তরিকের বিপরীত বাহু)

∴ AD = EF।

অতএব, ADE ও EFC ত্রিভুজ দুইটির

∠DAE = ∠FEC,

∠AED = ∠ECF

এবং AD = EF;

∴ ত্রিভুজ দুইটি সর্বসম। (স্বতঃ 6)

∴ AE = EC

.

.

.

উপপাদ্য 28 (Theorem 28)

.

বিবৃতি (Statement):

ত্রিভুজের যে কোন দুই বাহুর মধ্যবিন্দুদ্বয়ের সংযোগক সরলরেখা তৃতীয় বাহুর সমান্তরাল ও অর্ধেক।

[ The straight line joining the middle points of two sides of a triangle is parallel to the third side and equal to half of it. ]

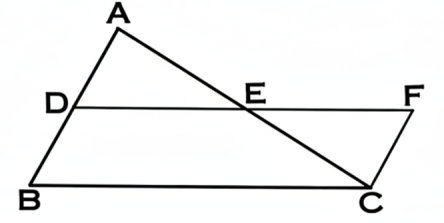
ABC ত্রিভুজে D ও E যথাক্রমে AB ও ACর মধ্যবিন্দু; DE উহাদের সংযোগক সরলরেখা।

প্রমাণ করিতে হইবে যে,

DE || BC এবং DE = $\frac{1}{2}$BC

.

অঙ্কন। DE কে বর্ধিত করিয়া বর্ধিতাংশ হইতে DEর সমান করিয়া EF লও। CF যোগ কর।

.

প্রমাণ। AED ও CEF ত্রিভুজদ্বয়ের

AE = EC, (কল্পনা)

DE = EF (অঙ্কন)

এবং ∠AED = বিপ্রতীপ ∠CEF;

∴ ত্রিভুজদ্বয় সর্বসম। (স্বতঃ 5)

∴ AD = FC, এবং ∠EAD = ∠ECF;

কিন্তু ইহারা একান্তর কোণ,

∴ AD || FC, অর্থাৎ DB || FC (উপ. 2)

আবার, DB = AD (কল্পনা)

এবং AD = FC; (প্রমাণিত)

∴ DB = FC

∴ DB ও FC সমান ও সমান্তরাল;

∴ DBCF একটি সামান্তরিক। (উপ. 24)

∴ DE || BC এবং DE = $\frac{1}{2}$DF = $\frac{1}{2}$BC

.

.

অনুশীলনী 58

[উপ. 26-28 বিষয়ক ]

.

1. ত্রিভুজের শীর্ষ হইতে ভূমি পর্যন্ত অঙ্কিত সরলরেখা অপর দুই বাহুর মধ্যবিন্দুদ্বয় সংযোগক সরলরেখা দ্বারা সমদ্বিখন্ডিত হয়। [ উপ. 27 এবং 28 এর সাহায্যে প্রমাণ কর।]

.

2. ত্রিভুজের দুই বাহুর মধ্যবিন্দুদ্বয়ের সংযোগক সরলরেখা (1) ত্রিভুজকে 1 ও 3 এর অনুপাতে বিভক্ত করে এবং (2) উহা ও তৃতীয় বাহুর সমদ্বিখন্ডক মধ্যমা পরস্পরকে সমদ্বিখন্ডিত করে।

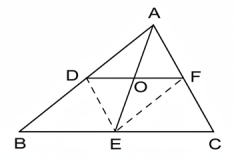ABC ত্রিভুজের D, E ও F যথাক্রমে AB, BC ও ACর মধ্যবিন্দু এবং DF ও AEর O ছেদবিন্দু। ED, EF যোগ কর।

.

প্রমাণ। (1) AD ও FE পরস্পর সমান ও সমান্তরাল (উপ. 28),

∴ ADEF একটি সামান্তরিক (উপ. 24); ∴ △DEF $\cong$ △DAF (উপ. 20)।

এইরূপ △DEF $\cong$ △DBE

এবং △DEF $\cong$ △FCE;

∴ △DAF : চতুর্ভুজ DBCF = 1 : 3

.

(2) AE ও DF, ADEF সামান্তরিকের কর্ণ বলিয়া উহারা পরস্পরকে O বিন্দুতে সমদ্বিখন্ডিত করিয়াছে (উপ. 21)।

.

3. ত্রিভুজের বাহুত্রয়ের মধ্যবিন্দুগুলি যোগ করিলে তিনটি সামান্তরিক এবং চারিটি সর্বসম ত্রিভুজ উৎপন্ন হয়।

.

4) সমকোণী ত্রিভুজের অতিভুজের মধ্যবিন্দু হইতে অতিভুজের মধ্যবিন্দু পর্যন্ত অঙ্কিত সরলরেখা অতিভুজের অর্ধেক।

[ The straight line joining the middle point of the hypotenuse of a right-angled triangle to the right angle is half the

hypotenuse.]

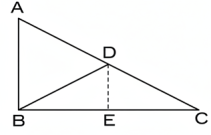
ABC ত্রিভুজ B সমকোণ এবং D, ACর মধ্যবিন্দু।

প্রমাণ করিতে হইবে যে, BD = $\frac{1}{2}$AC

D ও BCর মধ্যবিন্দু E যোগ কর।

প্রমাণ। AB || DE (উপ. 28)

∴∠DEC = অনুরূপ ∠ABE = 1 সমকোণ;

∴ ∠DEB = 1 সমকোণ। △DEB $\cong$  △DEC; (স্বতঃ 5)

∴ BD = DC = $\frac{1}{2}$AC

.

5. সমকোণী ত্রিভুজের একটি সূক্ষ্মকোণ অপরটির দ্বিগুণ হইলে, অতিভুজ ক্ষুদ্রতর বাহুর দ্বিগুণ হইবে।

ABC ত্রিভুজ (প্রশ্ন 4 এর চিত্র) ∠B সমকোণ, ∠A = 60°, ∠C = 30°, AB সূক্ষ্মতম বাহু এবং D, ACর মধ্যবিন্দু।

প্রমাণ। BD = ½AC (প্রশ্ন 4) = AD; ∴∠ABD = ∠A = 60°;

∴ তৃতীয় ∠ADB = 60°; ∴ AD = AB; AC = 2AD = 2AB

.

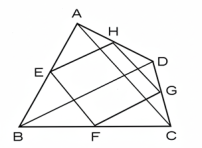6. কোন চতুর্ভুজের বাহুগুলির মধ্যবিন্দুগুলি ক্রমান্বয়ে যোগ করিলে একটি সামান্তরিক উৎপন্ন হইবে এবং উহার বাহুসমষ্টি ঐ চতুর্ভুজের কর্ণদ্বয়ের সমষ্টির সমান হইবে।

.

ABCD চতুর্ভুজের E, F, G, H যথাক্রমে AB, BC, CD, DAর মধ্যবিন্দু। EF, FG, GH, EH, AC, BD যোগ কর।

প্রমাণ। ∵ EH || BD || FG এবং

EH = ½BD = FG (উপ. 28)

∴ EFGH একটি সামান্তরিক

এবং EF + FG + GH + EH = ½AC + ½BD + ½AC + ½BD = AC + BD ।

.

7. চতুর্ভুজের বিপরীত বাহুদ্বয়ের মধ্যবিন্দু সংযোগক সরলরেখাদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।

[ প্রশ্ন 6 এর চিত্রে EG ও HF যোগ কর।

প্রমাণ। EFGH একটি সামান্তরিক (প্রশ্ন 6) এর EG ও HF উহার দুই কর্ণ। ∴ EG ও HF পরস্পরকে সমদ্বিখন্ডিত করে (উপ. 21) ]

.

8. ABCD একটি সামান্তরিক এবং E ও F যথাক্রমে AD ও BCর মধ্যবিন্দু। প্রমাণ কর যে, EC এবং AF, BD কে সমান তিন অংশে বিভক্ত করে। [উপ. 27 এর সাহায্যে প্রমাণ কর।]

.

9. সমদ্বিবাহু ত্রিভুজের ভূমির যে কোন বিন্দু হইতে অপর দুই বাহুর উপর পতিত লম্বদ্বয়ের সমষ্টি, ভূমির এক প্রান্ত হইতে বিপরীত বাহুর উপর পতিত লম্বের সমান।

.

10. সমবাহু ত্রিভুজের অভ্যন্তরস্থ যে কোন বিন্দু হইতে বাহুগুলির উপর পতিত লম্বদ্বয়ের সমষ্টি, যে কোন কৌণিক বিন্দু হইতে বিপরীত বাহুর উপর পতিত লম্বের সমান এবং ঐ সমষ্টি নিয়ত সমান (constant)।

.

11. ট্রাপিজিয়ামের অসমান্তরাল বাহুদ্বয়ের মধ্যবিন্দুদ্বয়ের সংযোগক সরলরেখা

(1) সমান্তরাল বাহুদ্বয়ের সহিত সমান্তরাল,

(2) কর্ণদ্বয়ের সমদ্বিখন্ডক এবং

(3) সমান্তরাল বাহুদ্বয়ের সমষ্টির অর্ধেক।

.

ABCD ট্রাপিজিয়াম AB ও DC সমান্তরাল বাহু এবং XY উহাদের মধ্যবিন্দুদ্বয় সংযোগক সরলরেখা।

Y দিয়া ABর সমান্তরাল EF টান; উহা যেন BC ও E বিন্দুতে এবং বর্ধিত AD কে F বিন্দুতে ছেদ করিল।

.

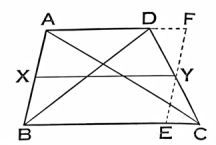এখন, (1) ∵ ABEF একটি সামান্তরিক, ∴ AB = FE

এবং ∵ △DYF $\cong$ △CYE (স্বতঃ 6),

∴ FY = YE; এবং ∴ AX || FY, ∴ XY || AD (উপ. 24)

এবং, XY || BC।

.

(2) ∵ X, ABর মধ্যবিন্দু এবং XY || BC,

∴XY, AC কে সমদ্বিখন্ডিত করে (উপ. 27)।

এবং XY, BD কে সমদ্বিখন্ডিত করে।

(3) XY = ½(AF + BE) = ½(AD + BC) (∵ DF = EC) ]

.

12. ABCD একটি ত্রিভুজদ্বয়ের বাহুদ্বয় কোণ সমান্তরাল উহার AP, BQ, CR ও DS লম্ব টান হইল। প্রমাণ কর যে, AP + CR = BQ + DS

.

13. AB একটি সরলরেখা O মধ্যবিন্দু। A, B ও O হইতে অপর একটি সরলরেখা PQR উপর যথাক্রমে AL, BM ও ON লম্ব টানা হইল। প্রমাণ কর যে, (1) যদি A ও B, PQর একই পার্শ্বে থাকে, তবে ON = ½(AL + BM) এবং (2) যদি A ও B, PQR বিপরীত পার্শ্বে থাকে, তবে ON = ½(AL – BM)

.

14. কোন সরলরেখার উপর দুইটি সমান ও সমান্তরাল সরলরেখার লম্ব অধিঃক্ষেপণ পরস্পর সমান।

.