Pair of Linear Equations in Two Variables

1.A pair of Linear Equations in two variables:

An equation of the form ax + by + c = 0, where a, b and c are real numbers, such that a and b are not both zero, is called a linear equation in two variables.

Two linear equations in same two variables x and y are called pair of linear equations in two variables.

Geometrical Representation of a Linear Equation

Geometrically, a linear equation in two variables can be represented as a straight line.

2x – y + 1 = 0

⇒ y = 2x + 1

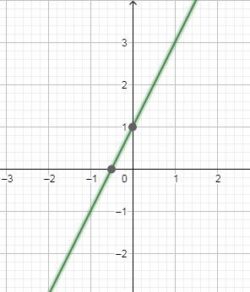
CBSE Class 10 Maths Notes Chapter 3 graph-1

Graph of y = 2x + 1

Plotting a Straight Line

The graph of a linear equation in two variables is a straight line. We plot the straight line as follows:

Pair of Linear Equations in Two Variables Class 10 Notes Chapter 3-1

2.Types of Polynomials based on Degree

Linear Polynomial

A polynomial whose degree is one is called a linear polynomial.

For example, 2x+1 is a linear polynomial.

Quadratic Polynomial

A polynomial of degree two is called a quadratic polynomial.

For example, 3x² + 8x + 5 is a quadratic polynomial.

Cubic Polynomial

A polynomial of degree three is called a cubic polynomial.

For example, 2x³ + 5x² + 9x + 15 is a cubic polynomial.

3.Graph of the polynomial x^n

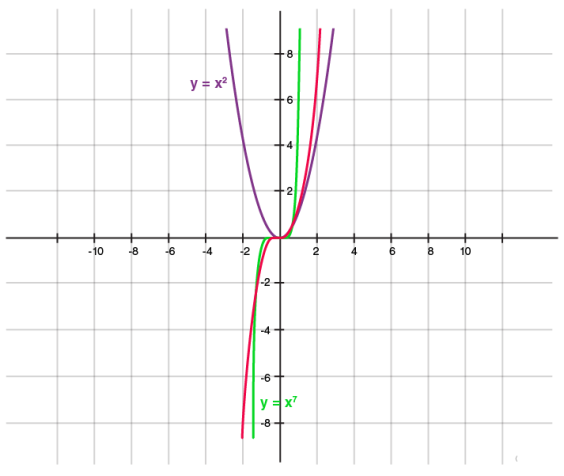
For a polynomial of the form y = xⁿ where n is a whole number:

as n increases, the graph becomes steeper or draws closer to the Y-axis

If n is odd, the graph lies in the first and third quadrants

If n is even, the graph lies in the first and second quadrants

The graph of y = −xⁿ is the reflection of the graph of y = xⁿ on the x-axis

4.Geometrical Meaning of Zeros of a Polynomial

Geometrically, zeros of a polynomial are the points where its graph cuts the x-axis.

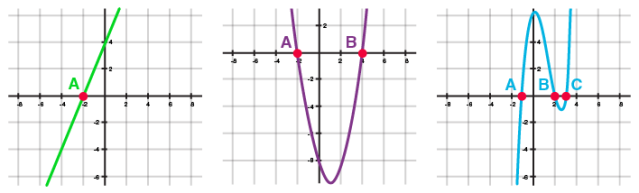
(i) One zero (ii) Two zeros (iii) Three zeros

Here A, B and C correspond to the zeros of the polynomial represented by the graphs.

Number of Zeros

In general, a polynomial of degree n has at most n zeros.

• A linear polynomial has one zero,

• A quadratic polynomial has at most two zeros.

• A cubic polynomial has at most 3 zeros.

5.The general form of a pair of linear equations in two variables is

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

where a₁, a₂, b₁, b₂, c₁ and c₂ are real numbers, such that

6.A system of linear equations in two variables represents two lines in a plane. For two given lines in a plane there could be three possible cases:

i.The two lines are intersecting, i. e., they intersect at one point.

ii.The two lines are parallel, i.e., they do not intersect at any real point.

iii.The two lines are coincident lines, i.e., one line overlaps the other line.

7.A system of simultaneous linear equations is said to be

Consistent, if it has at least one solution.

In-consistent, if it has no solution.

8.If the lines

i.Intersect at a point, then that point gives the unique solution of the system of equations. In this case system of equations is said to be consistent.

ii.Coincide (overlap), then the pair of equations will have infinitely many solutions. System of equations is said to be consistent.

iii.are parallel, then the pair of equations has no solution. In this case pair of equations is said to be inconsistent.

9.Solution of a pair of Linear Equations in two variable:

System of equations can be solved using Algebraic and Graphical Methods.

10.Graphical Method:

A linear equation in two variables is represented geometrically by a straight line.

The graph of a pair of linear equations in two variables is represented by two lines. Steps:

i.Draw the graphs of both the equations by finding two solutions for each.

ii.Plot the points and draw the lines passing through them to represent the equations.

iii.The behaviour of lines representing a pair of linear equations in two variables and the existence of solutions can be summarised as follows:

11.Algebraic Method:

Ratio of Coefficients	Graphical Representation	Nature of Solution	Defined as
$\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}$	Lines are intersecting	Unique solution	Consistent pair of equations
$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$	Lines are parallel	No solution	Inconsistent pair of equations
$\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$	Lines are coincident	Infinitely many solutions	Dependent (consistent) pair of equations

The most commonly used Algebraic Methods to solve a pair of linear equations in two variables are:

i.Substitution method

ii.Elimination method

iii.Cross-multiplication method

12.Substitution Method:

Steps followed for solving linear equations in two variables, using substitution method:

Step 1: Express the value of one variable, say y in terms of other variable x from either equation, whichever is convenient.

Step 2: Substitute the value of y in other equation and reduce it to an equation in one variable, i.e. in terms of x. There will be three possibilities:

a.If reduced equation is linear in x, then solve it for x to get a unique solution.

b.If reduced equation is a true statement without x, then system has infinite solutions.

c.If reduced equation is a false statement without x, then system has no solution.

Step 3: Substitute the value of x obtained in step 2, in the equation used in step 1, to obtain the value of y.

Step 4: The values of x and y so obtained is the coordinates of the solution of system of equations.

13.Elimination Method:

Steps followed for solving linear equations in two variables, by elimination Method:

Step 1: Multiply both the equations by some suitable non-zero constants to make the coefficients of variable x (or y) equal.

Step 2: Add or subtract both the equations to eliminate the variable whose coefficients are equal.

a.If an equation in one variable y (or x) is obtained, solve it for variable y (or x).

b.If a true statement involving no variable is obtained then the system has infinite solutions.

c.If a false statement involving no variable is obtained then the system has no solution.

Step 3: Substitute the value of variable y (or x) in either of the equation to get the value of other variable.

14.Cross Multiplication Method:

Steps followed for solving linear equations in two variables, by cross multiplication method:

Step 1: Write the equations in the general form.

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

Step 2: Arrange these in the following manner.

Here, the arrows between two numbers (coefficients) mean that they are to be multiplied and the second product is to be subtracted from the first product.

Step 3: Cross multiply:

$\frac{x}{b_{1} c_{2} - b_{2} c_{1}} = \frac{y}{a_{2} c_{1} - a_{1} c_{2}} = \frac{1}{a_{1} b_{2} - a_{2} b_{1}}$

a.Comparing (1) and (3), we get the value of x

$x = \frac{b_{1} c_{2} - b_{2} c_{1}}{a_{1} b_{2} - a_{2} b_{1}}$

b.Comparing (2) and (3), we get the value of y

$y = \frac{a_{2} c_{1} - a_{1} c_{2}}{a_{1} b_{2} - a_{2} b_{1}}$

From the above equations, obtain the value of x and y provided a₁b₂ – a₂b₁ ≠ 0.

15.Equations which are not linear but can be reduced to linear form by some suitable substitutions are called equations reducible to linear form.

Reduced equation can be solved by any of the algebraic method (substitution, elimination or cross multiplication) of solving linear equation.

16.While solving problems based on time, distance and speed; following knowledge may be useful:

If speed of a boat in still water = u km/hr,

Speed of the current = v km/hr Then,

Speed upstream = (u – v) km/hr

Speed downstream = (u + v) km/hr

17.Factorization of Polynomials

Quadratic polynomials can be factorized by splitting the middle term.

For example, consider the polynomial 2x² − 5x + 3

Splitting the middle term:

The middle term in the polynomial 2×2−5x+3 is -5x. This must be expressed as a sum of two terms such that the product of their coefficients is equal to the product of 2 and 3 (coefficient of x² and the constant term)

−5 can be expressed as (−2) + (−3), as −2 × −3 = 6 = 2 × 3

Thus, 2x² − 5x + 3 = 2x² − 2x − 3x + 3

Now, identify the common factors in individual groups

2x² − 2x − 3x + 3 = 2x (x−1) – 3 (x−1)

Taking (x−1) as the common factor, this can be expressed as:

2x (x−1) −3 (x−1) = (x−1) (2x−3)

18.Relationship between Zeroes and Coefficients of a Polynomial

For Quadratic Polynomial:

If α and β are the roots of a quadratic polynomial ax2+bx+c, then,

α + β = -b/a

Sum of zeroes = -coefficient of x /coefficient of x2

αβ = c/a

Product of zeroes = constant term / coefficient of x2

For Cubic Polynomial

If α, β and γ are the roots of a cubic polynomial ax3+bx2+cx+d, then

α + β + γ = -b/a

αβ + βγ + γα = c/a

αβγ = -d/a

19.Division Algorithm

To divide one polynomial by another, follow the steps given below.

Step 1: arrange the terms of the dividend and the divisor in the decreasing order of their degrees.

Step 2: To obtain the first term of the quotient, divide the highest degree term of the dividend by the highest degree term of the divisor Then carry out the division process.

Step 3: The remainder from the previous division becomes the dividend for the next step. Repeat this process until the degree of the remainder is less than the degree of the divisor.

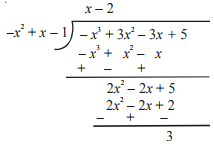
Important Questions

Multiple Choice questions-

1. Graphically, the pair of equations 7x – y = 5; 21x – 3y = 10 represents two lines which are

(a) intersecting at one point

(b) parallel

(d) coincident

2. The pair of equations 3x – 5y = 7 and – 6x + 10y = 7 have

(a) a unique solution

(b) infinitely many solutions

(d) two solutions

3. If a pair of linear equations is consistent, then the lines will be

(a) always coincident

(b) parallel

(d) intersecting or coincident

4. The pair of equations x = 0 and x = 5 has

(a) no solution

(b) unique/one solution

(d) infinitely many solutions

5. The pair of equation x = – 4 and y = – 5 graphically represents lines which are

(a) intersecting at (- 5, – 4)

(b) intersecting at (- 4, – 5)

(d) intersecting at (4, 5)

6. One equation of a pair of dependent linear equations is 2x + 5y = 3. The second equation will be

(a) 2x + 5y = 6

(b) 3x + 5y = 3

(d) 10x + 25y = 15

7.If x = a, y = b is the solution of the equations x + y = 5 and 2x – 3y = 4, then the values of a and b are respectively

(a) 6, -1

(b) 2, 3

(d) 19/5, 6/5

8. The graph of x = -2 is a line parallel to the

(a) x-axis

(b) y-axis

(d) none of these

9. The graph of y = 4x is a line

(a) parallel to x-axis

(b) parallel to y-axis

(d) passing through the origin

10. The graph of y = 5 is a line parallel to the

(a) x-axis

(b) y-axis

(d) none of these

Very Short Questions:

1.If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then find value of k.

2.Find the value of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 will have infinitely many solutions.

3.Do the equations 4x + 3y – 1 = 5 and 12x + 9y = 15 represent a pair of coincident lines?

4.Find the co-ordinate where the line x – y = 8 will intersect y-axis.

5.Write the number of solutions of the following pair of linear equations:

x + 2y – 8 = 0, 2x + 4y = 16

6.Is the following pair of linear equations consistent? Justify your answer.

2ax + by = a, 4ax + 2by – 2a = 0; a, b≠ 0

7.For all real values of c, the pair of equations

x – 2y = 8, 5x + 10y = c

have a unique solution. Justify whether it is true or false.

8.Does the following pair of equations represent a pair of coincident lines? Justify your answer.

$\frac{x}{2} + y + \frac{2}{5} = 0, 4 x + 8 y + \frac{5}{16} = 0 .$

9.If x = a, y = b is the solution of the pair of equation x – y = 2 and x + y = 4, then find the value of a and b.

10.

\frac{3}{2} x + \frac{5}{3} y = 7

9x – 10y = 14

Short Questions :

1.Solve: ax + by = a – b and bx – ay = a + b

2.Solve the following linear equations:

152x – 378y = -74 and -378x + 152y = -604

3.Solve for x and y

4.(i) For which values of a and b does the following pair of linear equations have an infinite number of solutions?

2x + 3y = 7

(a – b)x + (a + b)y = 3a + b – 2

(ii) for which value of k will the following pair of linear equations have no solution?

3x + y = 1

(2k – 1)x + (k – 1)y = 2k + 1

5.Find whether the following pair of linear equations has a unique solution. If yes, find the

7x – 4y = 49 and 5x – y = 57

6.Solve for x and y.

7.Solve the following pair of equations for x and y.

8.In ∆ABC, LA = x, ∠B = 3x, and ∠C = y if 3y – 5x = 30°, show that triangle is right angled.

9.In Fig. 3.1, ABCDE is a pentagon with BE|CD and BC||DE. BC is perpendicular to CD. If the perimeter of ABCDE is 21 cm. Find the value of x and y.

Diagram Description automatically generated

10.Five years ago, A was thrice as old as B and ten years later, A shall be twice as old as B. What are the present ages of A and B?

Long Questions :

1.Form the pair of linear equations in this problem and find its solution graphically: 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.

2.Show graphically the given system of equations

2x + 4y = 10 and 3x + 6y = 12 has no solution.

3.Solve the following pairs of linear equations by the elimination method and the substitution method:

(i) 3x – 5y – 4 = 0 and 9x = 2y + 7

(ii) $\frac{x}{2} + \frac{2 y}{3} = - 1$ and $x - \frac{y}{3} = 3$

4.Draw the graph of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.

5.A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days, she has to pay 31000 as hostel charges whereas a student B, who takes food for 26 days, pays 1180 as hostel charges. Find the fixed charges and the cost of food per day.

6.Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deduced for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?

7.8 men and 12 boys can finish a piece of work in 10 days while 6 men and 8 boys can finish it in 14 days. Find the time taken by one man alone and that by one boy alone to finish the work.

8.A boat covers 25 km upstream and 44 km downstream in 9 hours. Also, it covers 15 km upstream and 22 km downstream in 5 hours. Find the speed of the boat in still water and that of the stream.

Case Study Questions:

1.A part of monthly hostel charges in a college is fixed and the remaining depends on the number of days one has taken food in the mess. When a student Anu takes food for 25 days, she has to pay ₹ 4500 as hostel charges, whereas another student Bindu who takes food for 30 days, has to pay ₹ 5200 as hostel charges.

A picture containing text Description automatically generated

Considering the fixed charges per month by ₹ x and the cost of food per day by ₹ y, then answer the following questions.

i.Represent algebraically the situation faced by both Anu and Bindu.

a.x + 25y = 4500, x + 30y = 5200

b.25x + y = 4500, 30x + y = 5200

c.x – 25y = 4500, x – 30y = 5200

d.25x – y = 4500, 30x – y = 5200

ii.The system of linear equations, represented by above situations has.

a.No solution.

b.Unique solution.

c.Infinitely many solutions.

d.None of these.

iii.The cost of food per day is:

a.₹ 120

b.₹ 130

c.₹ 140

d.₹ 1300

iv.The fixed charges per month for the hostel is:

a.₹ 1500

b.₹ 1200

c.₹ 1000

d.₹ 1300

v.If Bindu takes food for 20 days, then what amount she has to pay?

a.₹ 4000

b.₹ 3500

c.₹ 3600

d.₹ 3800

2.From Bengaluru bus stand, if Riddhima buys 2 tickets to Malleswaram and 3 tickets to Yeswanthpur, then total cost is ₹ 46; but if she buys 3 tickets to Malleswaram and 5 tickets to Yeswanthpur, then total cost is ₹ 74.

A picture containing graphical user interface Description automatically generated

Consider the fares from Bengaluru to Malleswaram and that to Yeswanthpur as ₹ x and ₹ y respectively and answer the following questions.

i.1^st situation can be represented algebraically as:

a.3x – 5y = 74

b.2x + 5y = 74

c.2x – 3y = 46

d.2x + 3y = 46

ii.2^nd situation can be represented algebraically as:

a.5x + 3y = 74

b.5x – 3y = 74

c.3x + 5y = 74

d.3x – 5y = 74

iii.Fare from Bengaluru to Malleswaram is:

a.₹ 6

b.₹ 8

c.₹ 10

d.₹ 2

iv.Fare from Bengaluru to Yeswanthpur is:

a.₹ 10

b.₹ 12

c.₹ 14

d.₹ 16

v.The system of linear equations represented by both situations has:

a.Infinitely many solutions.

b.No solution.

c.Unique solution.

d.None of these.

Assertion reason questions-

1.Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

a.Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).

b.(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).

c.(C) Assertion (A) is true but reason (R) is false.

d.(d) Assertion (A) is false but reason (R) is true.

Assertion: The graph of the linear equations 3x+2y=12 and 5x-2y=4 gives a pair of intersecting lines.

Reason: The graph of linear equations a₁x + b₁y + c₁= 0 and a₂x + b₂y + c₂= 0 gives a pair of intersecting lines if a₁/a₂ ≠ b₁/b₂

2.Directions: In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

a.Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).

b.Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).

c.Assertion (A) is true but reason (R) is false.

d.Assertion (A) is false but reason (R) is true.

Assertion: If the pair of lines are coincident, then we say that pair of lines is consistent and it has a unique solution.

Reason: If the pair of lines are parallel, then the pairs has no solution and is called inconsistent pair of equations.

Answer Key-

Multiple Choice questions-

1.(b) -10

2.(d) a – 0, b = -6

3.(d) more than 3

4.(a) b – a + 1

5.(b) both negative

6.(a) cannot both be positive

7.(c) c and a have the same sign

8.(a) has no linear term and the constant term is negative.

9.(d) more than 4

10.(b) x² + 9x + 20

11.(a) both negative

Very Short Answer :

1.Since the given lines are parallel

2.The given system of equations will have infinitely many solutions if

\frac{c}{6} = \frac{- 1}{- 2} = \frac{2}{3}

which is not possible

∴ For no value of c, the given system of equations have infinitely many solutions.

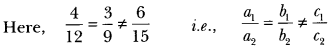
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 2

Given equations do not represent a pair of coincident lines.

4.The given line will intersect y-axis when x = 0.

∴0 – y = 8 ⇒ y = -8

Required coordinate is (0, -8).

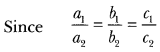
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 4

∴The given pair of linear equations has infinitely many solutions.

6.Yes,

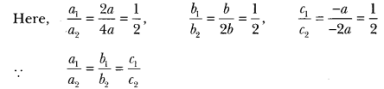
A picture containing diagram Description automatically generated

∴ The given system of equations is consistent.

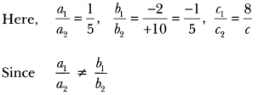
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 6

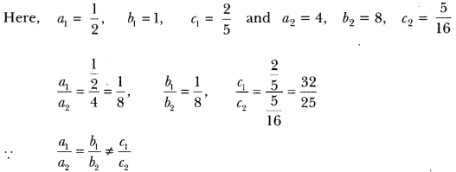
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 7

∴ The given system does not represent a pair of coincident lines.

x – y = 2 … (i)

x + y = 4 … (ii)

9.On adding (i) and (ii), we get 2x = 6 or x = 3

From (i), 3 – y ⇒ 2 = y = 1

a = 3, b = 1.

On comparing the ratios $\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}$ , and, $\frac{c_{1}}{c_{2}}$ find out whether the following pair of linear equations consistent or inconsistent. is consistent or inconsistent.

10.

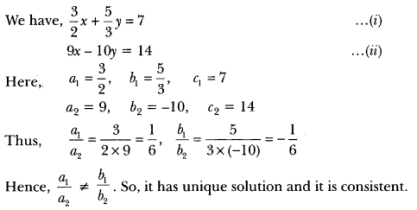
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 8

Short Answer :

1.The given system of equations may be written as

ax + by – (a – b) = 0

bx – ay – (a + b) = 0

By cross-multiplication, we have

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 13

Hence, the solution of the given system of equations is x = 1, y = -1

2.We have, 152x – 378y = -74 …(i)

-378x + 152y = -604 ……(ii)

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 14

Putting the value of x in (iii), we get

2 + y = 3 ⇒ y = 1

Hence, the solution of given system of equations is x = 2, y = 1.

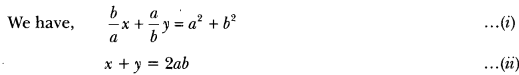
A picture containing text Description automatically generated

A picture containing background pattern Description automatically generated

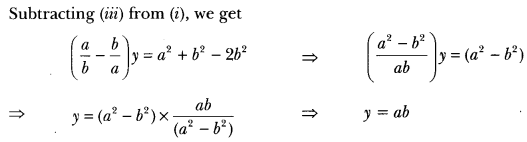
A picture containing text, device Description automatically generated

4.(i) We have, 2x + 3y = 7

(a – b) x + (a + b) y = 3a + b – 2 … (ii)

Here, a₁ = 2, b₁ = 3, c₁ = 7 and

a₂ = a – b, b₂ = a + b, c₂ = 3a + b – 2

For infinite number of solutions, we have

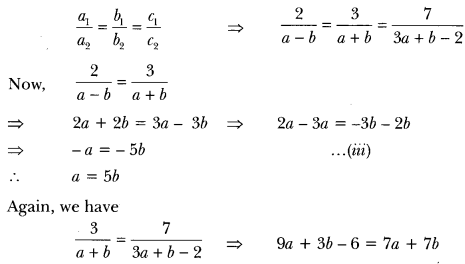
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 17

⇒ 9a – 7a + 3b – 75 -6 = 0 ⇒ 2a – 45 – 6 = 0 => 2a – 4b = 6

⇒ a – 2b = 3 …(iv)

Putting a = 5b in equation (iv), we get

56 – 2b = 3 or 3b = 3 i.e., b = $\frac{3}{3}$ =1

Putting the value of b in equation (ii), we get a = 5(1) = 5

Hence, the given system of equations will have an infinite number of solutions for a = 5 and b = 1.

(ii) We have, 3x + y = 1, 3x + y − 1 = 0 …(i)

(2k – 1) x + (k – 1) y = 2k + 1

⇒ (2k – 1) x + (k – 1) y – (2k + 1) = 0 ……(ii)

Here, a₁ = 3, b₁ = 1, C₁ = -1

a₂ = 2k – 1, b₂ = k – 1, C₂ = -(2k + 1)

For no solution, we must have

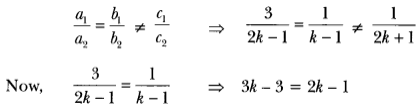
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 18

⇒ 3k – 2k = 3 – 1 ⇒ k = 2

5.Hence, the given system of equations will have no solutions for k = 2.

We have, 7x – 4y = 49 ……..(i)

and 5x – 6y = 57 ……..(ii)

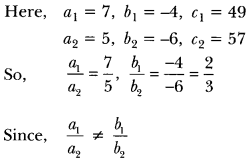
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 19

So, system has a unique solution.

Multiply equation (i) by 5 and equation (ii) by 7 and subtract

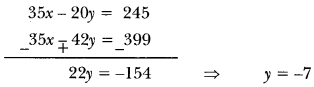
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 20

Put y = -7 in equation (ii)

5x – 6(-7)57 ⇒ 5x = 57 – 42 ⇒ x = 3

hence, x = 3 and y = -7.

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 22

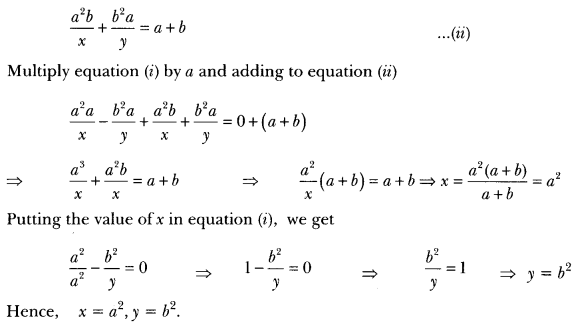
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 25

8.∠A + 2B + ∠C = 180°

(Sum of interior angles of A ABC) x + 3x + y = 180°

4x + y = 180° …(i)

3y – 5x = 30° (Given) …(ii) Multiply equation (i) by 3 and subtracting from eq. (ii), we get

-17x = – 510 = x = 910 = 30°

17 then _A = x = 30° and 2B = 3x = 3 X 30o = 90°

∠C = y = 180° – (∠A + ∠B) = 180° – 120° = 60°

∠A = 30°, ∠B = 90°, ∠C = 60° Hence ∆ABC is a right triangle right angled at B.

9.Since BC||DE and BE||CD with BC||CD.

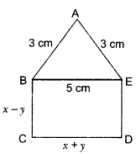
BCDE is a rectangle.

Opposite sides are equal BE = CD

∴ x + y = 5 …… (i)

DE = BC = x – y

Since the perimeter of ABCDE is 21 cm.

AB + BC + CD + DE + EA = 21

3 + x – y + x + y + x – y + 3 = 21 ⇒ 6 + 3x – y = 21

3x – y = 15 ….. (iii)

Adding (i) and (ii), we get

4x = 20 ⇒ x = 5

On putting the value of x in (i), we get y = 0

Hence, x = 5 and y = 0.

10.Let the present ages of B and A be x years and y years respectively. Then

B’s age 5 years ago = (x – 5) years

and A’s age 5 years ago = (- 5) years

(-5) = 3 (x – 5) = 3x – y = 10 …….(i)

B’s age 10 years hence = (x + 10) years

A’s age 10 years hence = (y + 10) years

y + 10 = 2 (x + 10) = 2x – y = -10 …….. (ii)

On subtracting (ii) from (i) we get x = 20

Putting x = 20 in (i) we get

(3 × 20) – y = 10 ⇒ y = 50

∴ x = 20 and y = 50

Hence, B’s present age = 20 years and A’s present age = 50 years.

Long Answer :

1.Let x be the number of girls and y be the number of boys.

According to question, we have

x = y + 4

⇒ x – y = 4 ……(i)

Again, total number of students = 10

Therefore, x + y = 10 …(ii)

Hence, we have following system of equations

x – y = 4

and x + y = 10

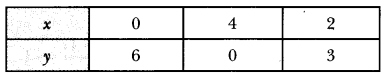
From equation (i), we have the following table:

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 32

From equation (ii), we have the following table:

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 33

Plotting this, we have

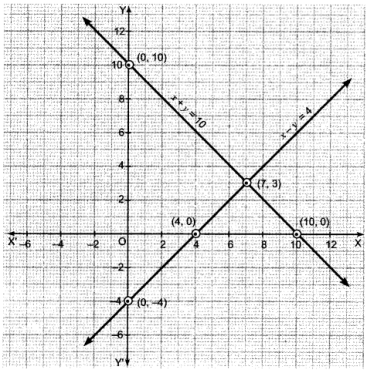
Chart, line chart Description automatically generated

Here, the two lines intersect at point (7,3) i.e., x = 7, y = 3.

So, the number of girls = 7

and number of boys = 3.

2.We have, 2x + 4y = 10

⇒ 4y = 10 – 2x ⇒ $y = \frac{5 - x}{2}$

Thus, we have the following table:

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 35

Plot the points A (1, 2), B (3, 1) and C (5,0) on the graph paper. Join A, B and C and extend it on both sides to obtain the graph of the equation 2x + 4y = 10.

We have, 3x + 6y = 12

⇒ 6y = 12 – 3x ⇒ $y = \frac{4 - x}{2}$

Thus, we have the following table :

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 36

Plot the points D (2, 1), E (0, 2) and F (4,0) on the same graph paper. Join D, E and F and extend it on both sides to obtain the graph of the equation 3x + 6y = 12.

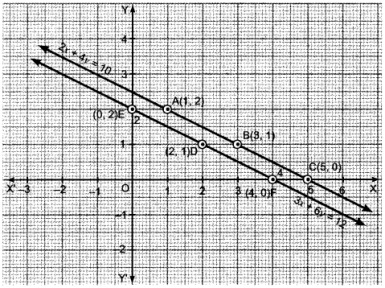
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 37

We find that the lines represented by equations 2x + 4y = 10 and 3x + y = 12 are parallel. So, the two lines have no common point. Hence, the given system of equations has no solution.

3.(i) We have, 3x – 5y – 4 = 0

⇒ 3x – 5y = 4 …….(i)

Again, 9x = 2y + 7

9x – 2y = 7 …(ii)

By Elimination Method:

Multiplying equation (i) by 3, we get

9x – 15y = 12 … (iii)

Subtracting (ii) from (iii), we get

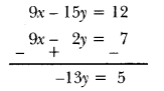
A picture containing text, clock Description automatically generated

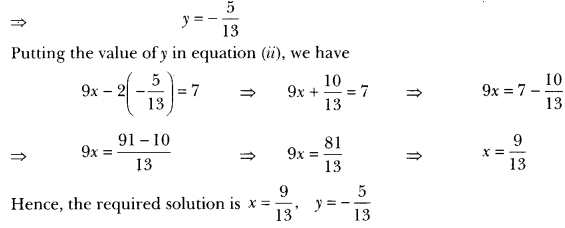
Table Description automatically generated

By Substitution Method:

Expressing x in terms of y from equation (i), we have

A picture containing text, receipt Description automatically generated

By Elimination Method:

Subtracting (ii) from (i), we have

5y = – 15 or y = – 55 = -3

Putting the value of y in equation (i), we have

3x + 4 × (-3) = -6 ⇒ 3x = – 6 + 12

∴ 3x – 12 = -6 ⇒ 3x = 6

∴ x = 63 = 2

Hence, solution is x = 2, y = -3.

By Substitution Method:

Expressing x in terms of y from equation (i), we have

Substituting the value of x in equation (ii), we have

∴ -5y = 9 + 6 = 15

$y = - \frac{15}{5} = - 3$

Putting the value of y in equation (i), we have

3x + 4 × (-3) = -6 ⇒ 3x – 12 = -6

∴ 3x = 12 – 6 = 6

∴ x = $\frac{6}{3}$ = 2

Hence, the required solution is x = 2, y = – 3.

4.We have,’ x – y + 1 = 0 and 3x + 2y – 12 = 0

Thus, x – y = -1 => x = y – 1 …(i)

3x + 2y = 12 => $x = \frac{12 - 2 y}{3}$ … (ii)

From equation (i), we have

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 40

From equation (ii), we have

Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 41

Plotting this, we have

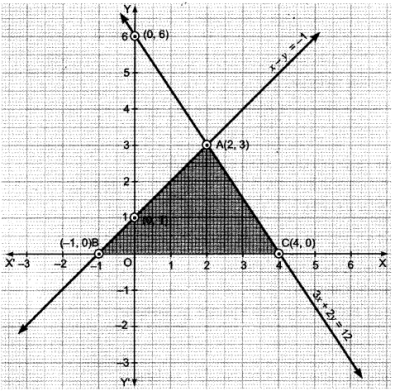
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 42

ABC is the required (shaded) region and point of intersection is (2, 3).

∴ The vertices of the triangle are (-1, 0), (4, 0), (2, 3).

5.Let the fixed charge be *x and the cost of food per day be by.

Therefore, according to question,

x + 20y = 1000 …(i)

x + 26y = 1180 …(ii)

Now, subtracting equation (ii) from (i), we have

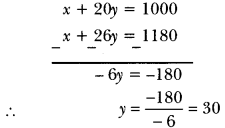
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 43

Putting the value of y in equation (i), we have

x + 20 x 30 = 1000 ⇒ x + 600 = 1000 ⇒ x = 1000 – 600 = 400

Hence, fixed charge is ₹400 and cost of food per day is ₹30.

6.Let x be the number of questions of right answer and y be the number of questions of wrong answer.

According to question,

3x – y = 40 … (i)

and 4x – 2y = 50

or 2x – y = 25 …(ii)

Subtracting (ii) from (i), we have

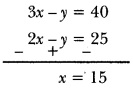
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 44

Putting the value of x in equation (i), we have

3 x 15 – y = 40 ⇒45 – y = 40

∴ y = 45 – 40 = 5

Hence, total number of questions is x + i.e.., 5 + 15 = 20.

7.Let one man alone can finish the work in x days and one boy alone can finish the work in y days

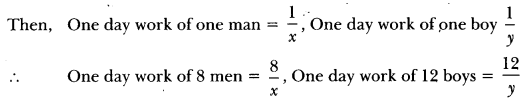
Chart, scatter chart Description automatically generated

A picture containing text, receipt Description automatically generated

Hence, one man alone can finish the work in 140 days and one boy alone can finish the work in 280 days.

8.Let the speed of the boat in still water be x km/h and that of the stream be y km/h. Then,

Speed upstream (x – y) km/h

Speed downstream (x + y) km/h

Table Description automatically generated with low confidence

Text Description automatically generated with medium confidence

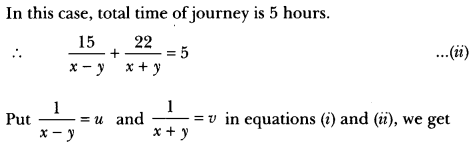
Diagram, text Description automatically generated with medium confidence

25u + 44v = 9 ⇒ 25u + 44v – 9 = 0 …(iii)

15u + 22v = 5 ⇒ 15u + 22v – 5 = 0 …(iv)

By cross-multiplication, we have

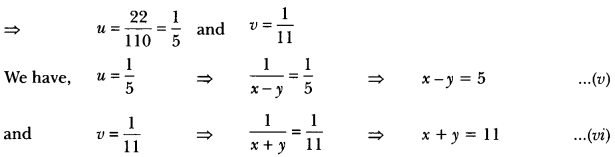
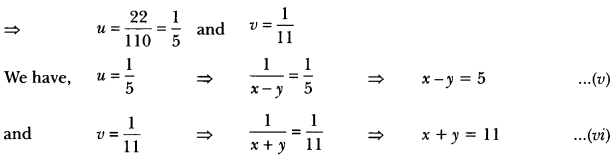
Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Solutions Answers 58

Solving equations (v) and (vi), we get x = 8 and y = 3.

Hence, speed of the boat in still water is 8 km/h and speed of the stream is 3 km/h.

Case Study Answers:

1.Answer :

i.(a) x + 25y = 4500, x + 30y = 5200

Solution:

For student Anu:

Fixed charge + cost of food for 25 days = ₹ 4500

i.e., x + 25y = 4500

For student Bindu:

Fixed charges + cost of food for 30 days = ₹ 5200

i.e., x + 30y = 5200

ii.(b) Unique solution.

Solution:

From above, we have a₁= 1, b₁ = 25

c₁ = -4500 and a₂ = 1, b₂ = 30, c₂ = -5200

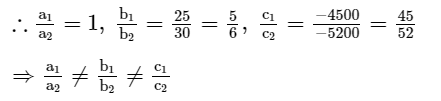
A picture containing chart Description automatically generated

Thus, system of linear equations has unique solution.

iii.(c) ₹ 140

Solution:

We have, x + 25y = 4500

and x + 30y = 5200

Subtracting (i) from (ii), we get

5y = 700 ⇒ y = 140

∴ Cost of food per day is ₹ 140

iv.(c) ₹ 1000

Solution:

We have, x + 25y = 4500

⇒ x = 4500 – 25 × 140

⇒ x = 4500 – 3500 = 1000

∴ Fixed charges per month for the hostel is ₹ 100

v.(d) ₹ 3800

Solution:

We have, x = 1000, y = 140 and Bindu takes food for 20 days.

∴ Amount that Bindu has to pay = ₹ (1000 + 20 × 140) = ₹ 3800

2.Answer :

i.(d) 2x + 3y = 46

Solution:

1^st situationcan berepresented algebraically as.

2x + 3y = 46

ii.(c) 3x + 5y = 74

Solution:

2^nd situation can be represented algebraically as:

3x + 5y = 74

iii.(b) ₹ 8

Solution:

We have, 2x + 3y = 46………(i)

3x + 5y = 74………(ii)

Multiplying (i) by 5 and (ii) by 3 and then subtracting, we get

10x – 9x = 230 – 222 ⇒ x = 8

∴ Fare from Bengaluru to Malleswaram is ₹ 8.

iv.(a) ₹ 10

Solution:

Putting the value of x in equation (i), we g

3y = 46 – 2 × 8 = 30 ⇒ y = 10

∴ Fare from Bengaluru to Yeswanthpur is ₹ 10

v.(c) Unique solution.

Solution:

We have, a₁= 2, b₁ = 3, c₁ = -46 and

a₂ = 3, b₂ = 5, C₂ = -74

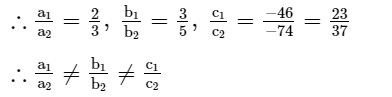
Chart Description automatically generated with low confidence

Thus system of linear equations has unique solution.

Assertion reason Answer-

1.(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).

2.(d) Assertion (A) is true but reason (R) is false.

Leave a Reply Cancel reply

Related Stories

Constructions

Probability

Statistics

You may have missed

বিজ্ঞানের জয়যাত্রা ও মানুষের ভবিষ্যৎ-Bigyaner jayayatra o manuser bhabisyat

বাংলার ঋতুচক্র-Banglar Rituchakra

প্রিয় গ্রন্থকার -“মানিক বন্দ্যোপাধ্যায়”-Priya granthakar- Manik bandyopadhay

তোমার প্রিয় কবি (জীবনানন্দ দাস )-Tomar priya kabi (Jibanananda das)