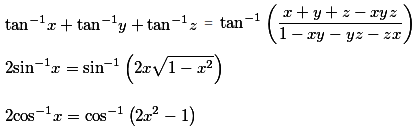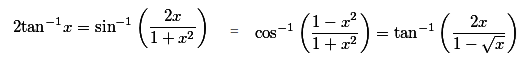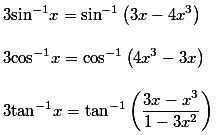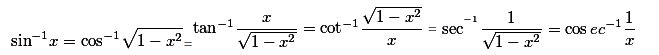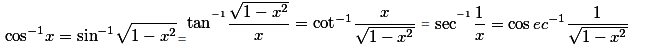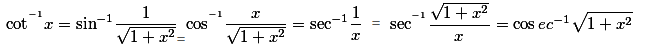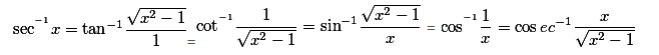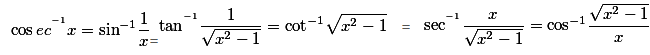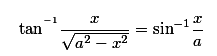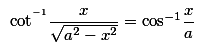Inverse-Trigonometric-Functions
INVERSE TRIGONOMETRIC FUNCTIONS
|
Functions |
Domain |
Range (Principal Value Branches) |
|
|
[-1, 1] |
|
|
|
[-1, 1] |
|
|
|
R- [-1, 1] |
|
|
|
R-[-1, 1] |
|
|
|
R |
|
|
|
R |
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
|
•
|
|
Important Questions
Multiple Choice questions-
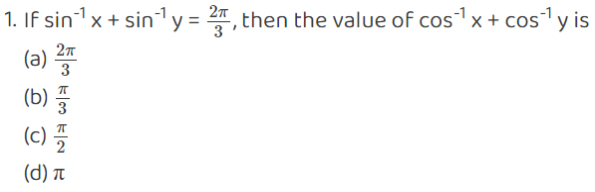


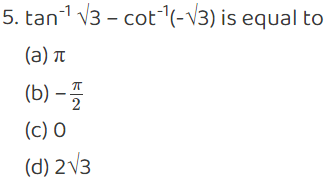
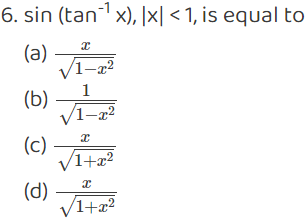
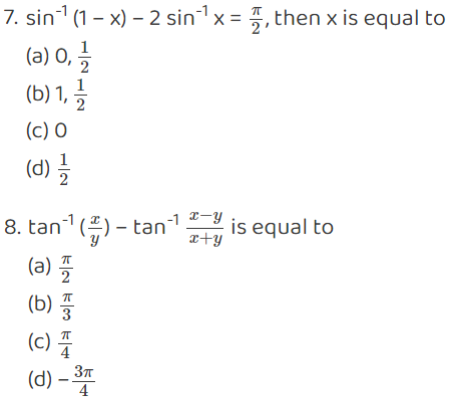

Very Short Questions:
cos-1 (cos 2π3 + sin-1 (sin 2π3)?
tan-1 (√3)- sec-1 (-2). (A.I.C.B.S.E. 2012)
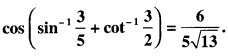
Short Questions:
![]()
Where – π4< x <π4, in the simples form.
![]()
![]()
![]()
![]()
![]()
(A.I.C.B.S.E. 2013)
![]()
Long Questions:
![]()
![]()
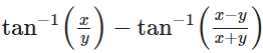
![]()
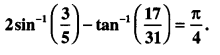
Assertion and Reason Questions:
1. Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes(a), (b), (c) and (d) as given below.
Assertion(A): A relation R = {(1, 1), (1, 3), (3, 1), (3, 3), (3, 5)} defined on the set A = {1,3,5} is reflexive.
Reason (R): A relation R on the set A is said to be transitive if for. (a, b) ∈R and (b, c)∈R, we have (a,c)∈R.
2. Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes(a), (b), (c) and (d) as given below.
Assertion (A): A relation R = {(a,b):|a−b| < 2}defined on the set A = {1,2,3,4,5} is reflexive.
Reason(R): A relation R on the set A is said to be reflexive if for (a,b) ∈R and(b,c)∈R, we have (a,c)∈R.
Case Study Questions:
1.
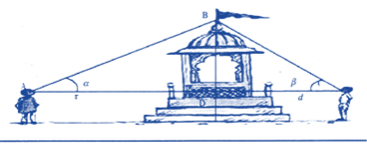
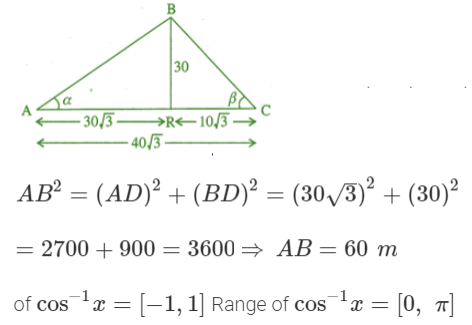
Two men on either side of a temple of 30 meters high observe its top at the angles of elevation α and β respectively, (as shown in the figure above). The distance between the two men is 40√3 meters and the distance between the first person A and the temple is 30√3 meters. Based on the above information answer the following :
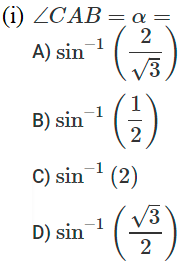
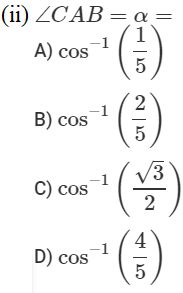
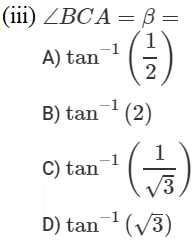
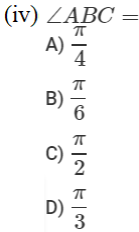
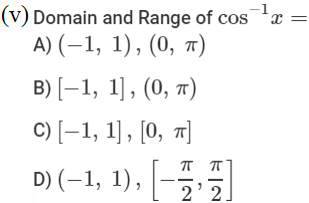
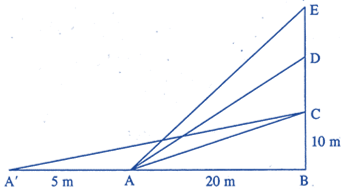
2. The Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. “A” is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby. Ram, Robert and Rahim suggested to the firm to place the hoarding board at three different locations namely C, D and E. “C” is at the height of 10 metres from the ground level.
For the viewer A, the angle of elevation of “D” is double the angle of elevation of “C”. The angle of elevation of “E” is triple the angle of elevation of “C” for the same viewer. Look at the figure given and based on the above information answer the following :
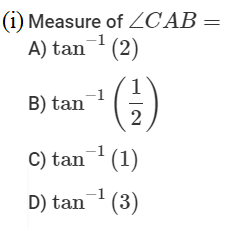
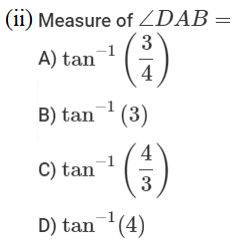
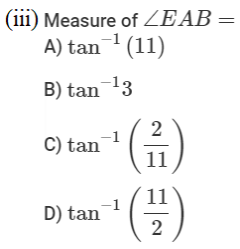

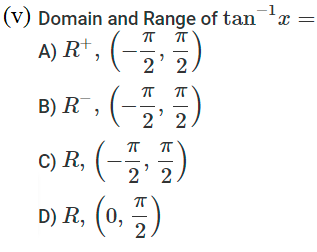
Case Study Answers:
1.
(i) (b)
Solution:
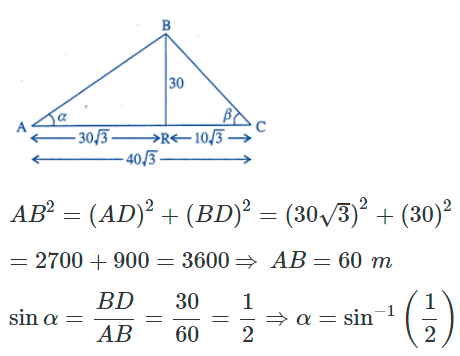
(ii) (c)
Solution:
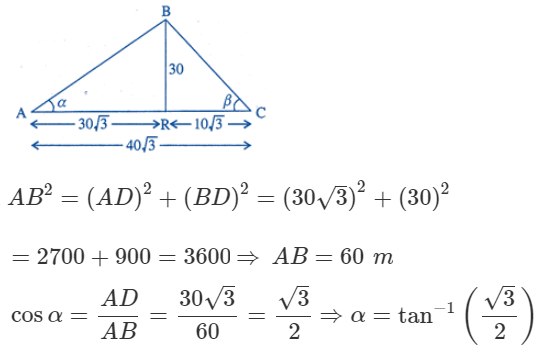
(iii) (d)
Solution:
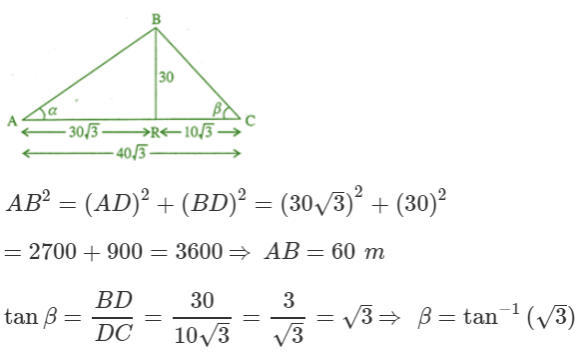
(iv) (c)
Solution:
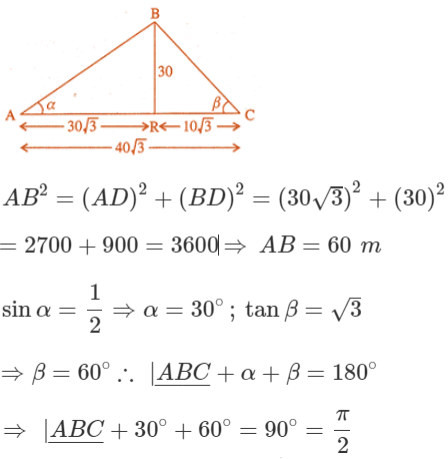
(v) (c)
Solution:
2.
Solution:
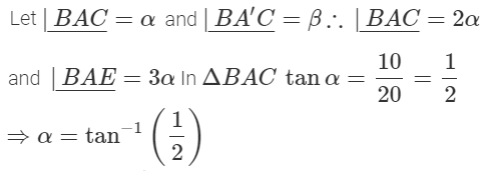
Solution:
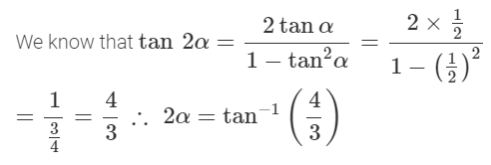
Solution:
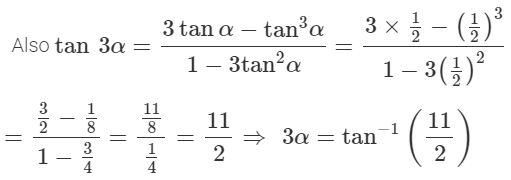
Solution:
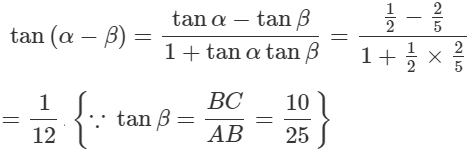
Solution:
Answer Key-
Multiple Choice questions-

Very Short Answer:
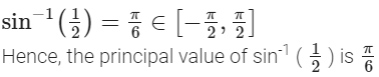
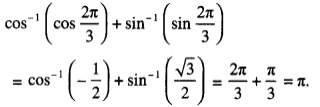
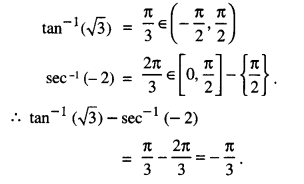
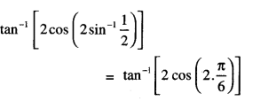
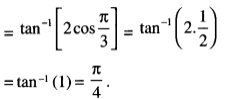
![]()
![]()
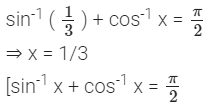
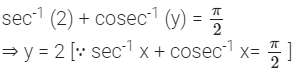
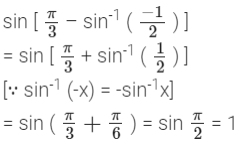
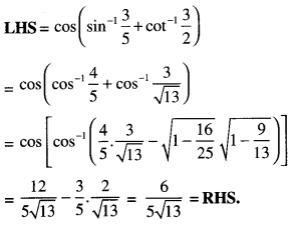
![]()
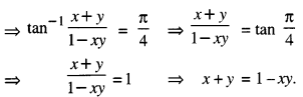
![]()
Short Answer:
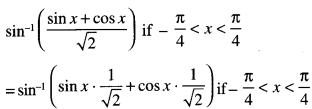
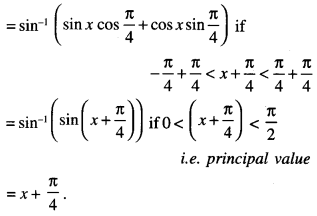
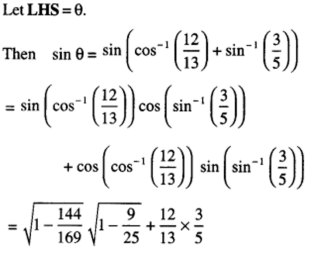
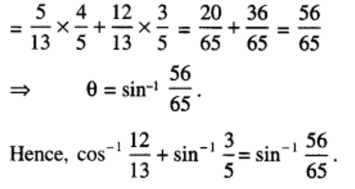
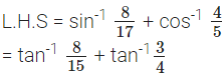
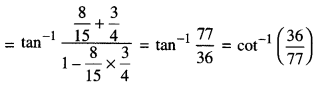
= R.H.S
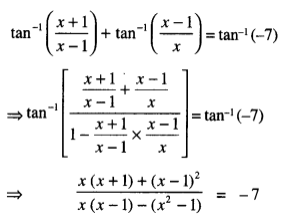
⇒ 2x2 – 8x + 8 = 0
⇒ x2– 4x + 4 = 0
⇒ (x – 2)2 = 0.
Hence, x = 2.
2 tan-1(sinx) = tan-1 (2 secx)
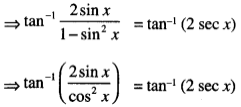
⇒ tan -1 (2sec x tan x) = tan-1 (2sec x)
⇒ 2 sec x tan x = 2 sec x
tan x = 1 [∵ sec x ≠0 ]
Hence, x= π2
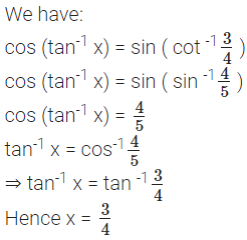
Put x = cos θ in RHS
As 1/2 ≤ x ≤ 1
RHS = cos-1 (4cos3 θ – 3cos θ),
= cos-1 (cos 3θ) = 3θ = 3cos-1 x = L.H.S
Long Answer:
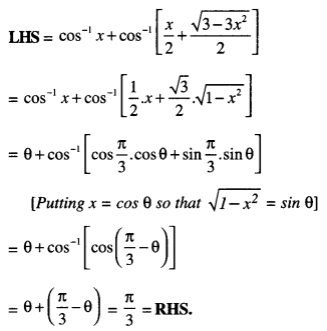
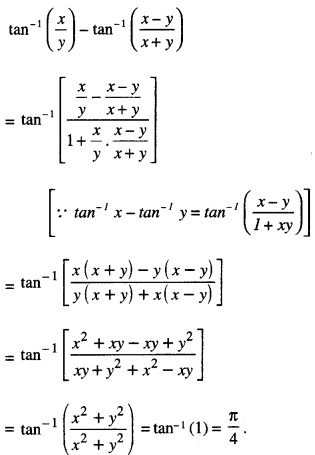
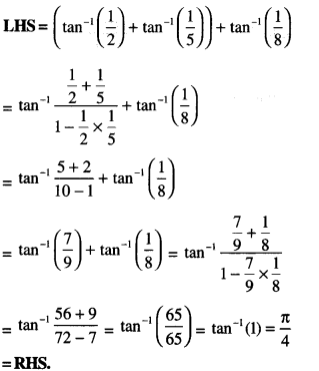
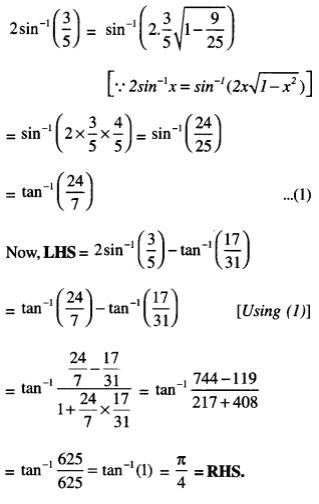
Assertion and Reason Answers:
1. (d) A is false and R is true.
Solution :
Given R = {(1,1),(1,3),(3,1),(3,3),(3,5)}
We know that Relation ‘R’ is reflexive on set A if ∀a∈A,(a,a)∈R
Here set A={1,3,5}
(1,1)∈R,(3,3)∈R
but (5,5)∉R
∴R is not reflexive
∴ Assertion A is false By definition of transition Relation, It is clear that given Reason R is true. Hence option (d) is the correct answer.
2.(c) A is true but R is false.
Solution:
Given R={(a,b):|a−b|<2}
= {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (1, 2), (2, 1), (2, 3), (3, 2), (3, 4). (4, 3), (4, 5), (5, 4)}.
Here (1,1)∈R, (2,2)∈R, (3,3)∈R, (4,4)∈R, (5,5)∈R
⇒ Relation R is reflexive on set A = {1,2,3,4,5}
∴ Assertion A is true We know that relation R is reflexive if (a,a) ∈R ∀ a ∈A
∴ Given Reason R is false Hence option (c) is the correct answer.