
Geometry-Formulas
জ্যামিতির – সূত্রাবলী
Geometry Formulas
(1) মাত্রা— দৈর্ঘ্য, প্রস্থ ও উচ্চতা বা বেধকে মাত্রা বলে।
(2) বিন্দু – যার দৈর্ঘ্য, প্রস্থ বা উচ্চতা নেই কিন্তু অবস্থান আছে তাকে বিন্দু বলে।
(3) তল— যার দৈর্ঘ্য ও প্রস্থ আছে কিন্তু উচ্চতা নেই তাকে তল বলে।
(4) রেখা— যার দৈর্ঘ্য আছে কিন্তু প্রস্থ বা উচ্চতা নেই তাকে রেখা বলে। রেখা হচ্ছে একটি বিন্দুর সঞ্ছার পথ।
(5) সরলরেখা— যে রেখা দিক পরিবর্তন করে না তাকে সরলরেখা বলে।
(6) বক্ররেখা— যে রেখা দিক পরিবর্তন করে তাকে বক্ররেখা বলে।
(7) সমান্তরাল সরলরেখা— একই সমতলে অবস্থিত দুই বা ততোধিক সরল রেখাকে উভয়দিকে বর্ধিত করলে তারা যদি কখনও মিলিত না হয় তবে তাদের সমান্তরাল সরলরেখা বলে।
(৪) কোণ— দুটি সরলরেখা একটি বিন্দুতে মিলিত হলে, ঐ মিলন বিন্দুতে কোণ উৎপন্ন হয়।
(9) সন্নিহিত কোণ— দুটি কোণের একটি সাধারণ বাহু থাকলে, সাধারণ বাহুর উভয় পার্শ্বের কোণদ্বয়কে পরস্পরের সন্নিহিত কোণ বলে।
(10) লম্ব— একটি সরলরেখা অপর একটি সরলরেখার উপর এমনভাবে দণ্ডায়মান হয় যে দুটি সন্নিহিত কোণ সমান হয় তখন একটি সরলরেখাকে অপরটির উপর লম্ব বলে।
(11) সমকোণ— দুটি সরলরেখা পরস্পর লম্ব হলে যে দুটি সন্নিহিত কোণ উৎপন্ন হয় তাদের প্রত্যেককে সমকোণ বলে।
(12) এক ডিগ্রী – এক সমকোণের 90 ভাগের 1 ভাগকে 1° (ডিগ্রী) বলে। 1° ডিগ্রী = 190সমকোণ ।
(13) সূক্ষ্মকোণ — 0° অপেক্ষা বড় কিন্তু 90° অপেক্ষা ছোট কোণকে সূক্ষ্মকোণ বলে। যেমন– 1°, 60°, 89° ইত্যাদি।
(14) স্থূলকোণ– 90° অপেক্ষা বড় কিন্তু 180° অপেক্ষা ছোট কোণকে স্থূলকোণ বলে। যেমন— 91°, 120°, 179° ইত্যাদি।
(15) সরল কোণ– যে কোণ দুই সমকোণের সমান তাকে সরলকোণ বলে। 1 সরলকোণ = 180° ।
(16) প্রবৃদ্ধকোণ— দুই সমকোণ অপেক্ষা বড় কিন্তু চার সমকোণ অপেক্ষা ছোট কোণকে প্রবৃদ্ধ কোণ বলে।
(17) পূরককোণ— দুটি কোণের সমষ্টি 90° হলে একটিকে অপরটির পূরককোণ বলে।
(18) সম্পূরক কোণ – দুটি কোণের সমষ্টি 180° হলে একটিকে অপরটির সম্পূরক কোণ বলে।
(19) বিপ্রতীপ কোণ— দুটি সরলরেখা পরস্পর ছেদ করলে ছেদ বিন্দুতে যে চারটি কোণ উৎপন্ন হয় তাদের যে কোন দুটি বিপরীত কোণের একটিকে অপরটির বিপ্রতীপ কোণ বলে।
(20) একান্তর কোণ— সমান্তরাল রেখার ছেদকের বিপরীত পার্শ্বে সন্নিহিত কোণ ছাড়া অপর অন্তঃকোণদ্বয়কে পরস্পরের একান্তর কোণ বলে।
(21) অনুরূপ কোণ– ছেদকের একই পার্শ্বে অন্তঃকোণ ও দূরবর্তী বহিঃকোণকে পরস্পরের অনুরূপ কোণ বলে।
(22) ত্রিভুজ— তিনটি সরলরেখা দ্বারা সীমাবদ্ধ সামতলিক ক্ষেত্রকে ত্রিভুজ বলে।
বাহুভেদে ত্রিভুজ তিন প্রকার– সমবাহু, সমদ্বিবাহু ও বিষমবাহু।
কোণভেদে তিন প্রকার— সূক্ষ্মকোণী, সমকোণী ও স্থূলকোণী।
(23) সমবাহু ত্রিভুজ— যে ত্রিভুজের তিনটি বাহু পরস্পর সমান তাকে সমবাহু ত্রিভুজ বলে।
(24) সমদ্বিবাহু ত্রিভুজ— যে ত্রিভুজের দুটি বাহু পরস্পর সমান তাকে সমদ্বিবাহু ত্রিভুজ বলে।
(25) বিষমবাহু ত্রিভুজ – যে ত্রিভুজের তিনটি বাহু অসমান তাকে বিষমবাহু ত্রিভুজ বলে।
(26) সূক্ষ্মকোণী ত্রিভুজ— যে ত্রিভুজের তিনটি কোণ সূক্ষ্মকোণ তাকে সূক্ষ্মকোণী ত্রিভুজ বলে।
(27) সমকোণী ত্রিভুজ– যে ত্রিভুজের একটি কোণ সমকোণ তাকে সমকোণী ত্রিভুজ বলে।
(28) স্থূলকোণী ত্রিভুজ – যে ত্রিভুজের একটি কোণ স্থূলকোণ তাকে স্থূলকোণী ত্রিভুজ বলে।
(29) সমকোণী সমদ্বিবাহু ত্রিভুজ – যে সমকোণী ত্রিভুজের দুটি বাহু পরস্পর সমান তাকে সমকোণী সমদ্বিবাহু ত্রিভুজ বলে।
(30) সদৃশকোণী ত্রিভুজ – একটি ত্রিভুজের তিনটি কোণ অপর একটি ত্রিভুজের তিনটি কোণের সঙ্গে যথাক্রমে সমান হলে ত্রিভুজ দুটিকে সদৃশকোণী ত্রিভুজ বলে।
(31) সদৃশ ত্রিভুজ – দুটি ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী হলে ত্রিভুজ দুটিকে সদৃশ ত্রিভুজ বলে।
(32) মধ্যমা – ত্রিভুজের যে কোন শীর্ষবিন্দু হতে বিপরীত বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাকে মধ্যমা বলে।
(33) উচ্চতা – ত্রিভুজের যে কোন শীর্ষবিন্দু হতে বিপরীত বাহুর উপর লম্বকে উচ্চতা বলে।
(34) দুটি ত্রিভুজ সর্বনম হওয়ার শর্ত
(i) বাহু, বাহু, বাহু সর্বসমতানুযায়ী
(ii) বাহু, কোণ, বাহু সর্বসমতানুযায়ী
(iii) কোণ, বাহু, কোণ সর্বসমতানুযায়ী
(35) চতুর্ভুজ— চারটি সরলরেখা দ্বারা সীমাবদ্ধ সামতলিক ক্ষেত্রকে চতুর্ভুজ বলে।
(36) বর্গক্ষেত্র— যে চতুভুজের চারটি বাহু পরস্পর সমান ও প্রতিটি কোণ সমকোণ (90°) তাকে বর্গক্ষেত্র বলে।
(37) আয়তক্ষেত্র— যে চতুভুজের বিপরীত বাহুগুলি সমান ও কোণগুলি সমকোণ তাকে আয়তক্ষেত্র বলে।
(38) সামান্তরিক— যে চতুর্ভুজের বিপরীত বাহুগুলি সমান্তরাল তাকে সামান্তরিক বলে।
(39) রম্বস— যে চতুর্ভুজের চারটি পরস্পর বাহু সমান কিন্তু কোণগুলি সমকোণ নয় তাকে রম্বস বলে।
(40) ট্রাপিজিয়ম— যে চতুর্ভুজের কেবল মাত্র এক জোড়া বিপরীত বাহু সমান্তরাল তাকে ট্রাপিজিয়ম বলে।
(41) সমদ্বিবাহু ট্রাপিজিয়ম— যে ট্রাপিজিয়মের তির্যক বাহু দুটি পরস্পর সমান তাকে সমদ্বিবাহু ট্রাপিজিয়ম বলে।
(42) বহুভুজ— তিন বা ততোধিক সরলরেখা দ্বারা সীমাবদ্ধ সামতলিক ক্ষেত্রকে বহুভুজ বলে।
(43) কুব্জ বহুভুজ— যে বহুভুজের অন্ততঃ একটি কোণ প্রবৃদ্ধ কোণ তাকে কুব্জ বহুভুজ বলে।
(44) সুষম বহুভুজ— যে বহুভুজের বাহুগুলি পরস্পর সমান তাকে সুষম বহুভুজ বলে।
(45) কর্ণ— কোন বহুভুজের বিপরীত কৌণিক বিন্দুর সংযোজক সরলরেখাকে কর্ণ বলে।
(46) বৃত্ত— একটি মাত্র বক্ররেখা দ্বারা সীমাবদ্ধ সামতলিক ক্ষেত্রের মধ্যাস্থিত কোন নির্দিষ্ট বিন্দু হতে বক্ররেখা পর্যন্ত অঙ্কিত সমস্ত সরলরেখার দূরত্ব সমান হলে ঐ সীমাবদ্ধ সামতলিক ক্ষেত্রকে বৃত্ত বলে। ব্যাস বৃত্তের বৃহত্তম জ্যা।
উপপাদ্য
Theorems
ভূমিকা (Introduction): জ্যামিতিতে আমরা সক্রিয়তার মাধ্যমে কয়েকটি ধর্ম জানতে পারি। এই ধর্মগুলিকে বলা হয় স্বতঃসিদ্ধ বা নিজে থেকে প্রমাণিত সত্য। স্বতঃসিদ্ধগুলিকে যুক্তি সহকারে প্রমাণ করার প্রয়োজন হয় না। অপরপক্ষে, এমন কয়েকটি জ্যামিতিক ধর্ম আছে যাদের যুক্তি দ্বারা প্রতিষ্ঠিত করা যায়। যখন আমরা কোনো জ্যামিতিক ধর্মকে যুক্তি সহকারে প্রমাণ করি, তখন যে ধর্মটি প্রমাণ করতে হবে সেটি, প্রমাণের পদ্ধতি এবং সিদ্ধান্তে উপনীত হওয়া—এই সমস্ত স্তরকে একত্রে উপপাদ্য বলে। সুতরাং, প্রমাণ সহ জ্যামিতিক ধর্মকে উপপাদ্য বলে।
প্রতিজ্ঞা (Propositions): প্রতিজ্ঞা বলতে আমরা বুঝি সেই সমস্ত বিবৃতি যেগুলি কোনো জ্যামিতিক ধর্ম প্রমাণ করতে অথবা কোনো জ্যামিতিক অঙ্কন করতে প্রস্তাব দেয়। দুই ধরনের প্রতিজ্ঞা আছে—উপপাদ্য ও সম্পাদ্য।
উপপাদ্য: যে প্রতিজ্ঞা যুক্তি সহকারে প্রমাণ করা যায় তাকে বলে উপপাদ্য ।
সম্পাদ্য: যে প্রতিজ্ঞায় জ্যামিতিক অঙ্কনের প্রয়োজন হয় তাকে বলে সম্পাদ্য।
জ্যামিতিক প্রতিজ্ঞার বিভিন্ন অংশ (Different parts of a proposition)
একটি জ্যামিতিক প্রতিজ্ঞার চারটি অংশ: (1) সাধারণ নির্বাচন (2) বিশেষ নির্বচন (3) অঙ্কন ও (4) প্রমাণ।
(1) সাধারণ নির্বাচন: স্বীকার এবং সিদ্ধান্তের সাধারণ বিবৃতিকে বলা হয় সাধারণ নির্বচন।
(2) বিশেষ নির্বচন: প্রতিজ্ঞার দ্বিতীয় অংশ বিশেষ নির্বচন সাধারণ নির্বচন অনুসারে চিত্র অঙ্কন করা হয়। চিত্রের নামকরণ অনুসারে স্বীকার এবং সিদ্ধান্তের বিবৃতিকে বলা হয় বিশেষ নির্বচন।
(3) অঙ্কন: প্রতিজ্ঞার প্রমাণের জন্য কিছু অঙ্কনের প্রয়োজন হতে পারে। এই অংশে অঙ্কনের বিবৃতি উল্লেখ করা হয়।
(4) প্রমাণ: প্রতিজ্ঞার এটাই শেষ অংশ। এই অংশে এক গুচ্ছ যুক্তি সহকারে প্রতিজ্ঞাটি প্রমাণ করা হয়।
বিপরীত উপপাদ্য (Converse theorem)
যদি দুটি উপপাদ্য এমন হয় যে প্রথমটির স্বীকার, দ্বিতীয়টির সিদ্ধান্ত হয় এবং প্রথমটির সিদ্ধান্ত দ্বিতীয়টির স্বীকার হয় তাহলে উপপাদ্য দুটির একটিকে অপরটির বিপরীত উপপাদ্য বলে।
অনুসিদ্ধান্ত (Corollary)
যদি কোনো উপপাদ্যের সিদ্ধান্ত থেকে সহজেই অন্য সিদ্ধান্তে উপনীত হওয়া যায়, তবে তাকে অনুসিদ্ধান্ত বলে।
একান্তর কোণ – অনুরূপ কোণ–বিপ্রতীপ কোণ, সমান্তরাল সরলরেখা ও ছেদকের ধর্ম
(i) অনুরূপ কোণগুলি সমান হয়
(ii) একান্তর কোণগুলি সমান হয়
(iii) ছেদকের একই পার্শ্বস্থ অন্তঃকোণদ্বয়ের সমষ্টি দুই সমকোণের সমান হয়।
বহিস্থ কোন বিন্দু থেকে কোন সরলরেখার উপর একটি এবং কেবলমাত্র একটিই লম্ব অঙ্কন করা যায়।
কোন সরলরেখার উপর কোন বিন্দু দিয়ে একটি এবং কেবলমাত্র একটিই লম্ব অঙ্কন করা যায়।
ত্রিভুজের ধর্ম
15. মধ্যমা ও ভরকেন্দ্র (Medians and Centroid)
যদি ΔABC-এর AD একটি মধ্যমা হয় এবং G ত্রিভুজের ভরকেন্দ্র হয়, তবে
(i) AG:GD = 2:1 (ii) AG = 23AD (iii) GD = 13AD.
16. অন্তঃকেন্দ্র (Incentre)
কোনো ত্রিভুজের কোণগুলির অন্তর্দ্বিখণ্ডকত্রয় সমবিন্দু অর্থাৎ একই বিন্দুতে মিলিত হয়। কোনো ত্রিভুজের কোণগুলির সমদ্বিখণ্ডকত্রয় যে বিন্দুতে মিলিত হয়, তাকে ত্রিভুজটির অন্তঃকেন্দ্র বলে।
অন্তঃকেন্দ্র থেকে ত্রিভুজের তিনটি বাহুই সমদূরবর্তী। অন্তঃকেন্দ্র সর্বদাই ত্রিভুজের অভ্যন্তরে অবস্থান করে।
ABC ত্রিভুজের I অন্তঃকেন্দ্র। বৃত্ত DEF অন্তবৃত্ত অর্থাৎ ABC ত্রিভুজের অন্তর্লিখিত বৃত্ত এবং ID = IE = IF অন্তব্যাসার্ধ। ত্রিভুজের বাহুগুলি অন্তবৃত্তের স্পর্শক।
17. পরিকেন্দ্র (Circumcenter)
কোন ত্রিভুজের বাহুগুলির লম্ব সমদ্বিখণ্ডকত্রয় যে বিন্দুতে পরস্পরকে ছেদ করে, সেই বিন্দুকে ত্রিভুজের পরিকেন্দ্র বলে।
কোনো ত্রিভুজের তিনটি কৌণিক বিন্দু দিয়ে অঙ্কিত বৃত্তকে ওই ত্রিভুজের পরিবৃত্ত বলে। পরিকেন্দ্র থেকে ত্রিভুজের কৌণিক বিন্দুগুলি সমদূরবর্তী এবং এই দূরত্বই হল পরিব্যাসার্ধ।
পরিকেন্দ্র সূক্ষ্মকোণী ত্রিভুজের ভিতরে, স্থূলকোণী ত্রিভুজের বাইরে অবস্থান করে। কিন্তু সমকোণী ত্রিভুজের ক্ষেত্রে অতিভুজের মধ্যবিন্দুই হল ওই ত্রিভুজের পরিকেন্দ্র। সমকোণী ত্রিভুজের অতিভুজ ওই ত্রিভুজের পরিবৃত্তের একটি ব্যাস।
18. লম্ববিন্দু (Orthocenter)
ত্রিভুজের শীর্ষবিন্দুগুলি থেকে বিপরীত বাহুগুলির ওপর অঙ্কিত লম্ব তিনটির সাধারণ ছেদবিন্দুকে লম্ববিন্দু (Orthocentre) বলে। সমবাহু ত্রিভুজের লম্ববিন্দু, পরিকেন্দ্র, অন্তঃকেন্দ্র ও ভরকেন্দ্র একই বিন্দু।
সমবিন্দু সংক্রান্ত উপপাদ্য – Theorems on Concurrence
সদৃশতা বিষয়ক উপপাদ্য – Theorems on similarity
একটি ত্রিভুজের তিনটি কণের পরিমাপ অপর একটি ত্রিভুজের তিনটি কণের পরিমাপের সঙ্গে সমান হলে ত্রিভুজদ্বয়কে সদৃশকোণী বলা হয়। দুটি ত্রিভুজ সদৃশকোণী হলে ত্রিভুজ দুটি সদৃশ হবে। দুটি ত্রিভুজ সদৃশ হলে ত্রিভুজ দুটির অনুরূপ বাহুগুলি সমানুপাতী হবে।
(a) ABC ত্রিভুজের AB ও AC বাহুর উপর P ও Q
এরূপ দুটি বিন্দু যে PQ || BC হবে।
আমরা পাই,
(i) APPB = AQQC (ii) APAB = AQAC (iii) ABPB = ACQC (iv) APAB = PQBC = AQAC
(b) ABC ত্রিভুজের AB ও AC বাহুর উপর P ও Q এরূপ দুটি বিন্দু যে APPB = AQQC হয়, তাহলে PQ || BC হবে।
(c) ΔABC ও ΔPQR – এর ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R হলে ABPQ = BCQR = CARP হবে।
(b) যদি ΔABC ও ΔDEF-এর বাহুগুলি এরূপ যে,
ABDE=BCEF=CAFD হয়, তাহলে PQ || BC হবে।
পিথাগোরাসের উপপাদ্য (Pythagoras’ Theorem)
(a) পিথাগোরাসের উপপাদ্য :
বিবৃতি: সমকোণী ত্রিভুজের অতিভুজের (সমকোণের বিপরীত বাহুর) উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল, ত্রিভুজের অপর দুটি বাহুর উপর অঙ্কিত বর্গক্ষেত্র দুটির ক্ষেত্রফলের সমষ্টির সমান।
ABC সমকোণী ত্রিভুজের
∠A সমকোণ হলে, BC2 = AB2 + AC2
∠B সমকোণ হলে, AC2 = AB2 + BC2
∠C সমকোণ হলে, AB2 = AC2 + BC2
b) পিথাগোরাসের উপপাদ্যের বিপরীত উপপাদ্য:
বিবৃতি: কোনো ত্রিভুজের একটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুটি বাহুর উপর অঙ্কিত বর্গক্ষেত্র দুটির ক্ষেত্রফলের সমষ্টির সমান হলে, ত্রিভুজটি সমকোণী হবে এবং বৃহত্তম বাহুর বিপরীত কোণটি সমকোণ হবে।
ABC ত্রিভুজের
BC2 = AB2 + AC2 হলে, ∠A সমকোণ
AC2 = AB2 + BC2 হলে, ∠B সমকোণ
AB2 = AC2 + BC2 হলে, ∠C সমকোণ
অ্যাপোলোনিয়াসের উপপাদ্য :
AB² + AC² = 2(AD² + BD²)
চতুর্ভুজ (Quadrilateral)
সামান্তরিকের ধর্ম (Properties of Parallelogram)
সংজ্ঞা: যে চতুর্ভুজের দুই জোড়া বিপরীত বাহু পরস্পর সমাস্তরাল তাকে সামান্তরিক বলে।
(a) সামান্তরিকের বিপরীত বাহুগুলি পরস্পর সমান, বিপরীত কোণগুলি পরস্পর সমান এবং প্রত্যেক কর্ণ সামান্তরিককে দুটি সর্বসম ত্রিভুজে বিভক্ত করে।
(b) সামান্তরিকের কর্ণ দুটি পরস্পরকে সমদ্বিখণ্ডিত করে।
ABCD সামান্তরিকের AD || BC, AB || DC এবং কর্ণ AC ও কর্ণ BD-এর ছেদবিন্দু O
সামান্তরিকের ধর্ম অনুসারে আমরা পাই,
(i) AB = DC, AD = BC. (ii) ∠A = ∠C, ∠B = ∠D. (iii) ΔABC ≅ ΔACD, ΔABD ≅ΔBCD. (iv) OA = OC, OB = OD.
দ্রষ্টব্য: সামান্তরিকের যে–কোনো বাহু সংলগ্ন কোণদ্বয়ের সমষ্টি 2 সমকোণ বা 180°; যেমন ABCD সামান্তরিক হলে, ∠A + ∠B = 180°.
(1) যে চতুর্ভুজের বিপরীত বাহুগুলি সমান, তা একটি সামান্তরিক।
(2) যে চতুর্ভুজের বিপরীত কোণগুলি সমান, তা একটি সামান্তরিক।
(3) কোনো চতুর্ভুজের একজোড়া যে–কোনো দুটি বিপরীত বাহু সমান ও সমান্তরাল হলে, চতুর্ভুজটি একটি সামান্তরিক হবে।
(4) যে চতুর্ভুজের কর্ণ দুটি পরস্পরকে সমদ্বিখণ্ডিত করে, তা একটি সামান্তরিক।
আয়তক্ষেত্র, বর্গক্ষেত্র এবং রম্বসের প্রত্যেকটি এক– একটি বিশেষ প্রকারের সামান্তরিক।
যে সামান্তরিকের চারটি বাহু (অথবা দুটি সন্নিহিত বাহু) সমান, তাকে রম্বস বলে।
যে সামান্তরিকের চারটি বাহু সমান এবং প্রত্যেকটি কোণ সমকোণ, তাকে বর্গক্ষেত্র বলে।
যে সামান্তরিকের প্রত্যেকটি কোণ সমকোণ, তাকে আয়তক্ষেত্র
যে চতুর্ভুজের কেবল এক জোড়া বিপরীত বাহু পরস্পর সমান্তরাল, তাকে ট্যাপিজিয়াম বলে। ট্যাপিজিয়ামের প্রত্যেক তির্যক বাহু সংলগ্ন কোণ দুটির সমষ্টি 180″। স্পষ্টত ট্রাপিজিয়াম সামান্তরিক নয়।
রম্বস একটি সামান্তরিক। সুতরাং সামান্তরিকের সকল ধর্মই রম্বসে বর্তমান।
ABCD একটি চতুর্ভুজ। O বিন্দু কর্ণদ্বয় AC ও BD-এর ছেদবিন্দু। চতুর্ভুজটি একটি সামান্তরিক হবে, যদি (i) AB = DC, AD = BC হয় ;
(ii) ∠A = ∠C, ∠B = ∠D হয়;
(iii) AB = DC, AB || DC
অথবা AD = BC, AD || BC হয়;
(iv) OA = OC, OB = OD হয়।
(i) সামান্তরিক এবং আয়তক্ষেত্র উভয়েরই কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
(ii) রম্বস এবং বর্গক্ষেত্র উভয়েরই কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
ভেদক ও মধ্যবিন্দু সংক্রান্ত উপপাদ্য (Transversal & Mid-point Theorem)
(a) ত্রিভুজের কোনো একটি বাহুর মধ্যবিন্দু দিয়ে দ্বিতীয় একটি বাহুর সমান্তরাল করে অঙ্কিত সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে এবং ত্রিভুজের বাহুগুলির দ্বারা সমান্তরাল সরলরেখাটির খণ্ডিতাংশ দ্বিতীয় বাহুর অর্ধেক হবে।
(b) ত্রিভুজের যে–কোনো দুটি বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক।
(c) যদি তিনটি বা তার বেশি সমান্তরাল সরলরেখা একটি ভেদক থেকে সমান সমান অংশ খণ্ডিত করে, তবে তারা অপর যে–কোনো ভেদক থেকেও সমান সমান অংশ খণ্ডিত করবে।
(i) ABC একটি ত্রিভুজ। P বিন্দু AB বাহুর মধ্যবিন্দু। P দিয়ে BC-এর সমান্তরাল করে অঙ্কিত সরলরেখা AC-কে Q বিন্দুতে ছেদ করে। আমরা পাই,
(a) AQ = QC(b) PQ = 12 BC
(ii) ABC ত্রিভুজের AB ও AC বাহুর মধ্যবিন্দু D ও E. আমরা পাই,
(a) DE || BC (b) DE = 12 BC
প্রয়োগ : ABC ত্রিভুজের BE ও CD দুটি মধ্যমা। DE = 4 সেমি হলে BC বাহুর দৈর্ঘ্য কত?
: BE ও CD দুটি মধ্যমা D ও E যথাক্রমে AB ও AC বাহুর মধ্যবিন্দু।
.:. DE = 12 BC বা, BC = 2.DE = 2 × 4 সেমি = ৪ সেমি।
ক্ষেত্রফল সংক্রান্ত উপপাদ্য (Theorems on Area)
(a) একই ভূমির উপর এবং একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত সামান্তরিকগুলির ক্ষেত্রফল সমান।
(b) কোনো ত্রিভুজ ও কোনো সামান্তরিক একই ভূমির উপর এবং একই সমান্তরাল যুগলের মধ্যে অবস্থিত হলে ত্রিভুজের ক্ষেত্রফল সামান্তরিকের ক্ষেত্রফলের অর্ধেক হবে।
(c) একই ভূমির উপর এবং একই সমান্তরাল যুগলের মধ্যে অবস্থিত ত্রিভুজগুলির ক্ষেত্রফল সমান।
(d) সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজগুলি যদি একই ভূমির উপর এবং ভূমির একই পার্শ্বে অবস্থিত হয়, তবে তারা একই সমান্তরাল যুগলের মধ্যে অবস্থিত হবে।
(i) সামান্তরিকের ক্ষেত্রফল = ভূমি × উচ্চতা।
ABCD সামান্তরিকের BC বাহুর (বা BC বাহুর বর্ধিতাংশের উপর A (বা D) শীর্ষ থেকে AP (বা DQ) লম্ব হলে ABCD সামান্তরিকের ক্ষেত্রফল = BC x AP = BC x DQ.
(∵AD || BC ∴AP = DQ)
আবার, AB বাহুর (বা AB বাহুর বর্ধিতাংশের) উপর C থেকে অঙ্কিত লম্ব CR হলে ABCD সামান্তরিকের ক্ষেত্রফল = AB × CR.
(ii) ত্রিভুজের ক্ষেত্রফল = 12 × ভূমি × উচ্চতা।
12× কোনো একটি বাহু × ওই বাহুর উপর বিপরীত শীর্ষ থেকে অঙ্কিত লম্ব।
ABC ত্রিভুজের BC, CA ও AB বাহুর উপর যথাক্রমে AD, BE ও CF লম্ব হলে ΔABC- এর ক্ষেত্রফল
12× BC × AD = 12× CA × BE = 12× AB × CF.
(iii) দুটি ত্রিভুজের একই শীর্ষবিন্দু এবং একই ভূমি (বা সমান ভূমি) হলে ক্ষেত্রফল সমান হবে। একটি ত্রিভুজের যে–কোনো মধ্যমা ত্রিভুজকে যে দুটি ত্রিভুজে বিভক্ত করে, তাদের ক্ষেত্রফল সমান। যেমন, AD যদি ABC ত্রিভুজের একটি মধ্যমা হয়, তবে ΔABD = ΔACD. [∵উভয় ত্রিভুজের সমান ভূমি এবং একই শীর্ষ]
(iv) ABC ত্রিভুজের ভরকেন্দ্র G হলে ΔGAB = ΔGBC = ΔGCA = 13ΔABC.
(v) ABCD সামান্তরিকের কর্ণদ্বয়ের ছেদবিন্দু O হলে ΔABC = ΔADC = ΔBCD = ΔBAD = 12সামান্তরিক ABCD
ΔOAB=ΔOBC= ΔOCD = ΔOAD = 14 সামান্তরিক ABCD.
বহুভুজ
বহুভুজ (Polygon): কয়েকটি রেখাংশ দ্বারা সীমাবদ্ধ সামতলিক ক্ষেত্রকে বহুভুজ বলে।
বাহুর সংখ্যার তারতম্য অনুসারে বহুভুজের নামকরণ করা হয়। ত্রিভুজ হল তিনটি বাহুবিশিষ্ট বহুভুজ এবং চতুর্ভুজ হল চারটি বাহুবিশিষ্ট বহুভুজ।
কয়েকটি বহুভুজের দৃষ্টান্ত হল:
পঞ্চভুজ (Pentagon) অর্থাৎ যে বহুভুজের পাঁচটি বাহু থাকে।
ষড়ভুজ (Hexagon) অর্থাৎ যে বহুভুজের ছয়টি বাহু থাকে।
সপ্তভুজ (Heptagon) অর্থাৎ যে বহুভুজের সাতটি বাহু থাকে।
অষ্টভুজ (Octagon) অর্থাৎ যে বহুভুজের আটটি বাহু থাকে।
নবভুজ (Nonagon) অর্থাৎ যে বহুভুজের নয়টি বাহু থাকে।
দশভুজ (Decagon) অর্থাৎ যে বহুভুজের দশটি বাহু থাকে।
কুব্জ বহুভুজ (Convex Polygon)
যে বহুভুজে কোনো প্রবৃদ্ধকোণ থাকে না তাকে কুব্জ বহুভুজ বলে। অন্য কথায় বলা যেতে পারে যে, কুব্জ বহুভুজের প্রত্যেকটি অন্তঃকোণ 2 সমকোণ অপেক্ষা ক্ষুদ্রতর। সাধারণভাবে বহুভুজ বলতে কুব্জ বহুভুজকেই বোঝায়।
সুষম বহুভুজ (Regular Polygon)
যে বহুভুজের সব বাহু পরস্পর সমান এবং সব কোণ পরস্পর সমান তাকে সুষম বহুভুজ বলে।
দ্রষ্টব্য: যে বহুভুজের সব বাহু পরস্পর সমান তাকে সমবাহু বহুভুজ (equilateral polygon) বলে। আবার যে বহুভুজের সব কোণ পরস্পর সমান তাকে সদৃশকোণী বহুভুজ (equiangular polygon) বলে। কোনো বহুভুজ যুগপৎ সমবাহু ও সদৃশকোণী হলে, তাকে সুষম বহুভুজ বলে।
বেশির ভাগ ক্ষেত্রেই দেখা যায় যে, কোনো বহুভুজের বাহুর দৈর্ঘ্যগুলি সমান হলে তার কোণগুলিও সমান হয়। যেমন, সমবাহু ত্রিভুজের তিনটি কোণই 60° করে, বর্গক্ষেত্রের প্রত্যেকটি কোণ 90° করে, সুষম পঞ্চভুজের প্রত্যেকটি কোণ 108° করে, সুষম ষড়ভুজের প্রত্যেকটি কোণ 120° করে। তবে এর ব্যতিক্রমও আছে। যেমন, রম্বসের চারটি বাহু পরস্পর সমান কিন্তু তার চারটি কোণ পরস্পর সমান নয়। সুতরাং, রম্বসকে সুষম বহুভুজ বলা যাবে না।
(1) একটি বহিঃকোণের মান =360°n ; যেখানে n = বাহুর সংখ্যা
(2) একটি অন্তঃকোণ =[2n−4n] সমকোণ = (2n − 4) x 90°n।
(3) একটি অন্তঃকোণের মান = (180° – একটি বহিঃকোণ)
(4) মোট বহিঃকোণের পরিমাণ = 360° [বাহুর সংখ্যা যাই হোক না কেন]
(5) মোট অন্তঃকোণের পরিমাণ = (2n – 4) x 90°
(6) কর্ণের সংখ্যা = n(n−3)2 ; যেখানে n = বাহুর সংখ্যা।
(7) কোনো বহুভুজের বাহুগুলিকে একই ক্রমে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণগুলির সমষ্টি চার সমকোণ হবে।
(8) কোনো সুষম বহুভুজের একটি বহিঃস্থ কোণ x° হলে বহুভুজটির বাহুসংখ্যা = 360°x°
(9) কেনো সুষম বহুভুজের একটি অন্তঃকোণ x° হলে বহুভুজটির বাহুসংখ্যা = 360°180°−x°
কোন্ ক্ষেত্রে সুষম বহুভুজের প্রত্যেক অন্তঃকোণ প্রত্যেক বহিঃকোণ অপেক্ষা বৃহত্তর হয়?
তিনটি বাহুবিশিষ্ট সুষম বহুভুজের (অর্থাৎ সমবাহু ত্রিভুজের) প্রত্যেক বহিঃকোণ = 36003 =120° এবং প্রত্যেক অন্তঃকোণ = 180° – 120° = 60°
এক্ষেত্রে, অন্তঃকোণ বহিঃকোণ অপেক্ষা ছোটো।
চারটি বাহুবিশিষ্ট সুষম বহুভুজের (অর্থাৎ বর্গক্ষেত্রের) প্রত্যেক বহিঃকোণ = 36004 =90° এবং প্রত্যেক অন্তঃকোণ = 180° – 90° = 90° । এক্ষেত্রে, অন্তঃকোণ এবং বহিকোণ সমান।
আবার, যখন সুষম বহুভুজের বাহুসংখ্যা চারের বেশি, অর্থাৎ যখন n > 4 তখন প্রত্যেক বহিঃকোণ
= 3600n <90° অর্থাৎ, সন্নিহিত অন্তঃকোণ 90° অপেক্ষা বৃহত্তর। এক্ষেত্রে অন্তঃকোণ, বহিঃকোণ অপেক্ষা বৃহত্তর।
পূরকের একটি অন্তঃকোণ এবং সংলগ্ন বহিঃকোণের যোগফল 180° ।
বহুভুজের কর্ণ (Diagonals of a Polygon)
কোনো বহুভুজের যে–কোনো শীর্ষবিন্দুর পাশাপাশি দুটি শীর্ষবিন্দু ছাড়া অপর যে–কোনো শীর্ষবিন্দুর সঙ্গে যদি ওই শীর্ষবিন্দুটিকে যুক্ত করা হয় তাহলে যেসমস্ত রেখাংশ পাওয়া যায়, তাদের ওই বহুভুজের কর্ণ বলে।
n-সংখ্যক বাহুবিশিষ্ট বহুভুজের কর্ণের সংখ্যা হয় n(n−1) 2 − n
বহুভুজের অন্তঃকোণ এবং বহিঃকোণ সম্বন্ধে কয়েকটি জ্ঞাতব্য বিষয় (Some information about the interior and the exterior angles of polygons)
যে–কোনো বহুভুজে যতগুলি বাহু থাকে ঠিক ততগুলিই কোণ থাকে। যেমন, যে বহুভুজের বাহুর সংখ্যা 10 তার কোণের সংখ্যা 10.
বহুভুজের কোণ বলতে তার অন্তঃকোণ বোঝায়।
(1) n-সংখ্যক বাহুবিশিষ্ট বহুভুজের অন্তঃকোণগুলির সমষ্টি (2n – 4) সমকোণ অর্থাৎ (2n – 4) x 90°.
(2) n-সংখ্যক বাহুবিশিষ্ট সুষম বহুভুজের প্রত্যেকটি অন্তঃকোণের মান (2n−4)n সমকোণ অর্থাৎ
, (2n−4)x90°n
দ্রষ্টব্য: সুষম বহুভুজের প্রতিটি কোণের মান সমান বলে কোণের সমষ্টিকে কোণের সংখ্যা দ্বারা ভাগ করে এক–একটি কোণের মান নির্ণয় করা যায়। বহুভুজটি সুষম না হলে প্রত্যেকটি কোণ সমান হত না।
(3) যে–কোনো বহুভুজের একটি অন্তঃকোণ এবং একটি বহিঃকোণের সমষ্টি 180° বা 2 সমকোণ।
(4) যে–কোনো বহুভুজের বাহুগুলি একই ক্রমে বর্ধিত করলে, যে বহিঃকোণগুলি উৎপন্ন হয়, তাদের সমষ্টি চার সমকোণের সমান।
(5) n-সংখ্যক বাহুবিশিষ্ট কোনো সুষম বহুভুজের প্রত্যেকটি বহিঃকোণের পরিমাণ 4n সমকোণ অর্থাৎ, 3600n।
দ্রষ্টব্য: সমগ্র আলোচনায় আমরা বহুভুজ বলতে কুব্জ বহুভুজ (অর্থাৎ যে বহুভুজে কোনো প্রবৃদ্ধ কোণ নেই) ধরে নিয়েছি।
বৃত্তের ধর্ম
বৃত্ত সম্পর্কিত (চাপ ও জ্যা বিষয়ক) উপপাদ্য –Theorems on Circle – Related to Arc and Chord
(ii) ব্যাস বৃত্তের বৃহত্তম জ্যা। পরিধি বৃত্তের বৃহত্তম চাপ।
(iii) O-কেন্দ্রীয় বৃত্তের AB একটি জ্যা। যদি D বিন্দু AB-এর মধ্যবিন্দু হয়, তবে OD⊥AB
(iv) O-কেন্দ্রীয় বৃত্তের AB একটি জ্যা। যদি OD⊥AB হয়, তবে AD = BD.
আমরা পাই, OA2= OD2 + AD2 = OD2 + (12AB)2
(v) বৃত্তের সমান সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
(vi) বৃত্তের কেন্দ্র থেকে সমদূরবর্তী জ্যা সমান।
বৃত্তের ব্যাসার্ধ কোনো স্পর্শকের উপরে স্পর্শবিন্দুতে লম্ব হয়।
বৃত্তস্থ কোণ সংক্রান্ত উপপাদ্য – Theorems regarding angles in the segment of a circle
(i)একই বৃত্তচাপের উপর অবস্থিত পরিধিস্থ কোণ (বা বৃত্তস্থ কোণ) x° হলে, কেন্দ্রস্থ কোণ হবে 2x° বৃত্তের একই চাপের উপর অবস্থিত কেন্দ্রস্থ কোণ x° হলে, পরিধিস্থ কোণ হবে 12 x°
(ii) একই বৃত্তাপের উপর অবস্থিত দুটি পরিধিস্থ কোণ x° ও y° হলে, x° = y°
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য – Theorems regarding cyclic quadrilateral
ABCD একটি বৃত্তস্থ চতুর্ভুজ হলে ∠A + ∠C = 180° এবং ∠B + ∠D = 180°.
স্পর্শক বিষয়ক উপপাদ্য – Theorems regarding tangent to a circle
যদি A এবং B কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে C বিন্দুতে স্পর্শ (অন্তঃস্থভাবে বা ‘বহিঃস্থভাবে) করে, তবে A, B, C সমরেখ।
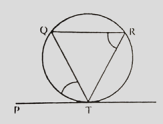
PT2 = PQ × PR
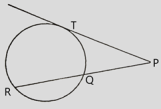
Note: যদি দুটি বৃত্তের ব্যাসার্ধ যথাক্রমে R এবং r হয়, এবং তাদের কেন্দ্রদ্বয়ের দূরত্ব D হয় তবে,
(i) সরল সাধারণ স্পর্শকের দৈর্ঘ্য = √D2− (R−r)2
(ii) তীর্যক সাধারণ স্পর্শকের দৈর্ঘ্য = √D2− (R+r)2
(iii) দুটি বৃত্তে মোট 3 টি স্পর্শক অঙ্কন করা যায়, যদি বৃত্ত দুটি পরস্পরকে স্পর্শ করে।
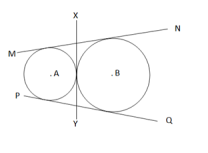
(iv) দুটি বৃত্তে মোট 4 টি (2 টি সরল ও 2 টি তির্যক) স্পর্শক অঙ্কন করা যায়, যদি বৃত্ত দুটি স্পর্শ না করে।
স্পর্শবিন্দু ছাড়া স্পর্শকের কোনো কিছুই বৃত্তের উপর অবস্থিত নয়।




