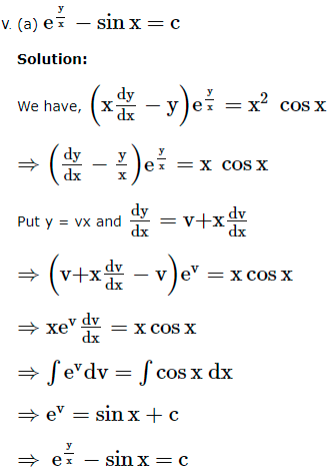Differential-Equations
DIFFERENTIAL EQUATIONS
Multiple Choice questions-
![]()
(a) 3
(b) 2
(c) 1
(d) not defined.
2. The order of the differential equation:
![]()
(a) 2
(b) 1
(c) 0
(d) not defined.
3. The number of arbitrary constants in the general solution of a differential equation of fourth order is:
(a) 0
(b) 2
(c) 3
(d) 4.
4. The number of arbitrary constants in the particular solution of a differential equation of third order is:
(a) 3
(b) 2
(c) 1
(d) 0.
5. Which of the following differential equations has y = c1 ex + c2 e-x as the general solution?
(a) d2ydx2 + y = 0
(b) d2ydx2 – y = 0
(c) d2ydx2 + 1 = 0
(d) d2ydx2 – 1 = 0
6. Which of the following differential equations has y = x as one of its particular solutions?
(a) d2ydx2 – x² dydx + xy = x
(b) d2ydx2 + x dydx + xy = x
(c) d2ydx2 – x² dydx + xy = 0
(d) d2ydx2 + x dydx + xy = 0
7. The general solution of the differential equation dydx = ex+y is
(a) ex + e-y = c
(b) ex + ey = c
(c) e-x + ey = c
(d) e-x + e-y = c.
8. Which of the following differential equations cannot be solved, using variable separable method?
(a) dydx + ex+y + e-x+y
(b) (y² – 2xy) dx = (x² – 2xy) dy
(c) xydydx = 1 + x + y + xy
(d) dydx + y = 2.
9. A homogeneous differential equation of the form dydx = h(xy) can be solved by making the substitution.
(a) y = vx
(b) v = yx
(c) x = vy
(d) x = v
10. Which of the following is a homogeneous differential equation?
(a) (4x + 6y + 5)dy – (3y + 2x + 4)dx = 0
(b) xy dx – (x³ + y²)dy = Q
(c) (x³ + 2y²) dx + 2xy dy = 0
(d) y² dx + (x² – xy – y²)dy = 0.
Very Short Questions:
dydx = ex+y (C.B.S.E. Sample Paper 2019-20)
ydydx – 2x = y3e-y
Short Questions:
dydx + y = cos x – sin x (Outside Delhi 2019)
dxdy + x = (tan y + sec2y). (Outside Delhi 2019 C)
Long Questions:
x2 + y2 = a2. (N.C.E.R.T.)
{(x,y): x2 + y2< 8, x2< 2y}. (C.B.S.E. Sample Paper 2018-19)
Case Study Questions:
1. If the equation is of the form ![]() where P, Q are functions of x, then the solution of the differential equation is given by ye
where P, Q are functions of x, then the solution of the differential equation is given by ye![]() is called the integrating factor (I.F.).
is called the integrating factor (I.F.).
Based on the above information, answer the following questions.
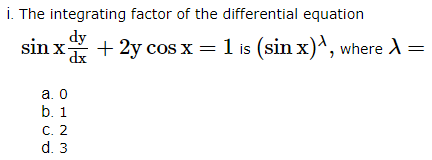
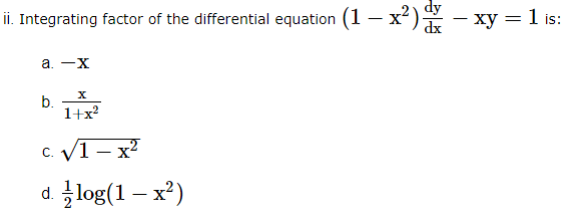
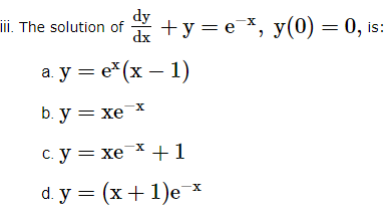
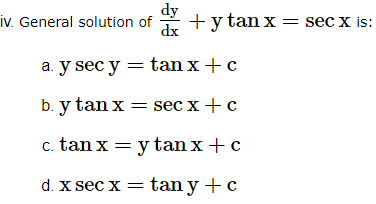
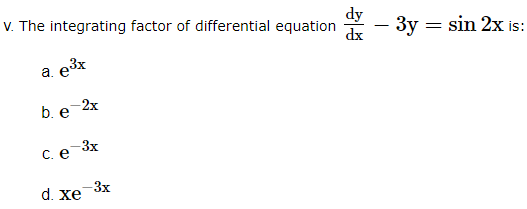
2. If the equation is of the form ![]() where f(x, y), g(x, y) are homogeneous functions of the same degree in x and y, then put y = vx And
where f(x, y), g(x, y) are homogeneous functions of the same degree in x and y, then put y = vx And 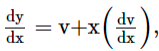 so that the dependent variable y is changed to another variable v and then apply variable separable method.
so that the dependent variable y is changed to another variable v and then apply variable separable method.
Based on the above information, answer the following questions.
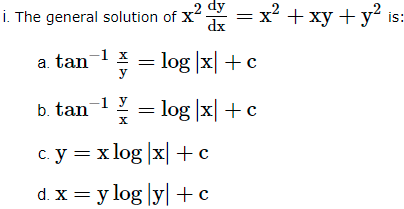
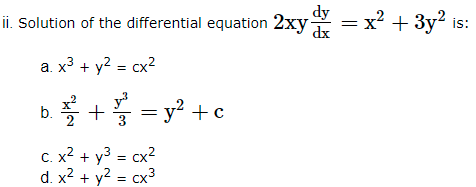
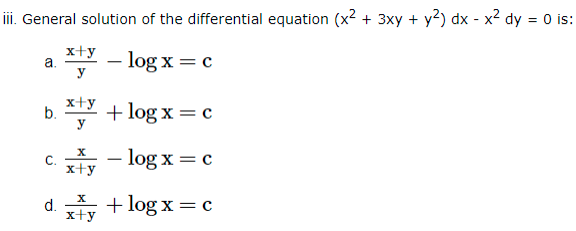
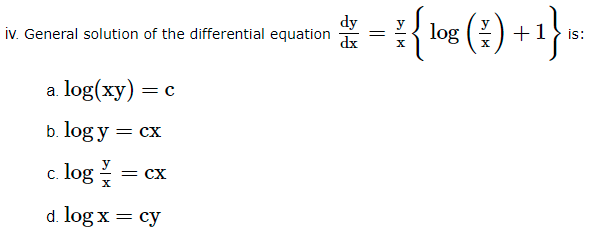
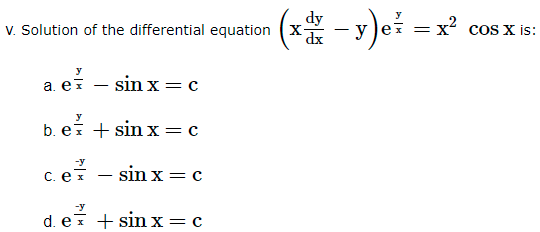
Answer Key-
Multiple Choice questions-
Very Short Answer:
We have: y= b(x + a) …(1)
Diff. w.r.t. x, b.
Again diff. w.r.t. x, d2ydx2 = 0,
which is the reqd. differential equation.
We have: dydx = ex+y
⇒ e–ydy = ex dx [Variables Separable
![]()
⇒– e-y + c = ex
⇒ ex + e-y = c.
The given equation can be written as.
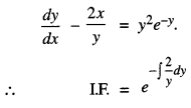
![]()
We have: y – a sin (3x – b) …(1)
Diff. W.r.t y dydx = a cos (3x – b) .3
= 3a cos (3x – b)
d2ydx2 = -3a sin (3x – b) 3
= -9a sin (3x – b)
= -9y [Using (1)]
d2ydx2 + 9y = 0,m
which in the reqd. differential equation.
Short Answer:
We have: y = e2x (a + bx) …(1)
Diff. w.r.t. x, dydx = e2x (b) + 2e2x (a + bx)
⇒dydx = be2x + 2y ………….. (2)
Again diff. w.r.t. x,
d2ydx2 = 2be2x + 22x
d2ydx2 = 2 (dydx–2y)+dydx
[Using (2)]
Hence, d2ydx2 -4 dydx + 4y = 0, which is the reqd. differential equation.
The given differential equation is:
dydx + y = cos x – sin x dx Linear Equation
∴ I.F. = e∫1dx = ex
The solution is :
y.ex = ∫ (cos x — sin x) ex dx + C
⇒y.ex = ex cos x + C
or y = cos x + C e-x
The given differential equation is:
dxdy + x = (tany + sec2y).
Linear Equation
∵ I.F. = Jldy = ey
∴ The solution is:
x. ey = ∫ ey (tan y + sec2y)dy + c
⇒ x. ey = ey tan y + c
= x = tan y + c e-y, which is the reqd. solution.
Long Answer:

log x = -log (1 + v2) + log C
x(1 + v2) = C
x(1 + y2x2)=C
x2 + y2 = C.

![]()
= tan-1 x + C
When y = 0, x = 1,
then 0 = π4 + C
C = π4
∴ y (1 + x2) = tan -1 x –π4
![]()
We have: y = aebx + 5 + 5 …(1)
Diff. w.r.t. x, dydx = aebx + 5. (b)
dydx = dy ……(2) [Using (1)]]
Again diff. w.r.t x.,
d2ydx2 = b dydx ………(3)
Dividing (3) by (2),
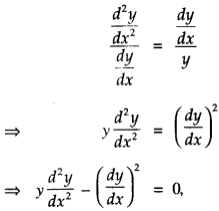
which is the required differential equation.
The given differential equation is:
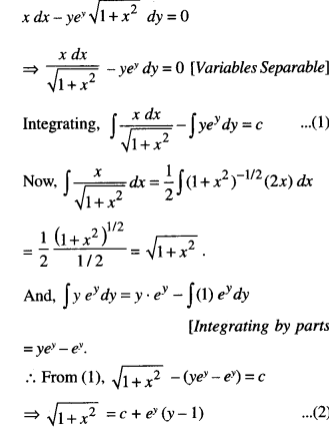
When x = 0, y = 1, ∴ 1 = c + c(0) ⇒ c = 1.
Putting in (2), √1 + x2= 1 + ey(y -1),
which is the reqd. particular solution.
Case Study Answers:
1. Answer :
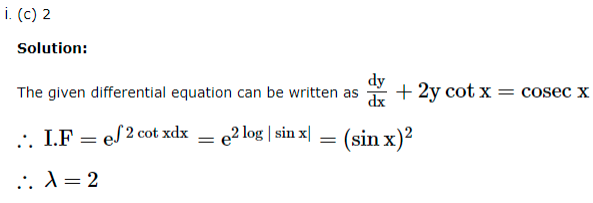
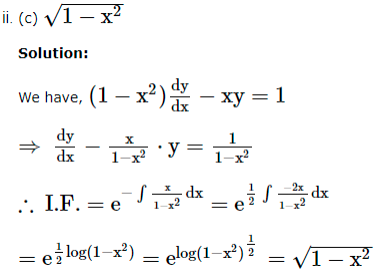
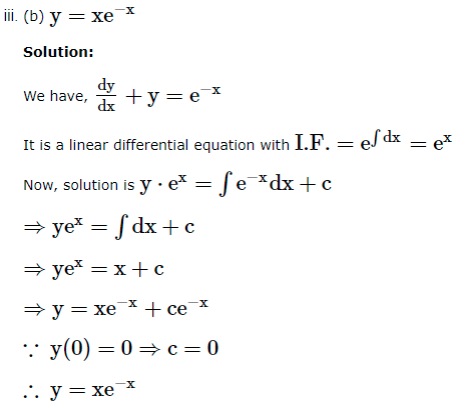
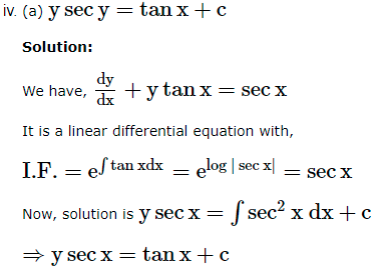
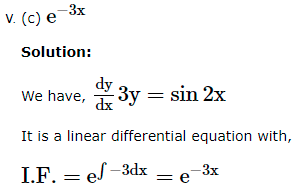
2. Answer :