DETERMINANTS

Top Definitions

1.To every square matrix A = [a_ij], a unique number (real or complex) called the determinant of the square matrix A can be associated. The determinant of matrix A is denoted by det(A) or |A| or

Δ

2.Only square matrices can have determinants.

3.A determinant can be thought of as a function which associates each square matrix to a unique number (real or complex).

f : M → K is defined by f(A) = k, where A $\in$ M set of square matrices and k $\in$ K set of numbers (real or complex).

4.Let A = [a] be a matrix of order 1, then the determinant of A is defined to be equal to a.

5.Determinant of order 2

Diagram Description automatically generated

6.Determinant of order 3

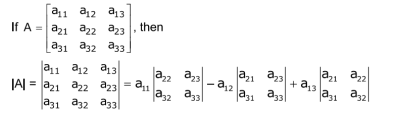
Chart, schematic Description automatically generated

7.Minor of an element a_¡j Of A determinant is the determinant obtained by deleting its i^th row and j^th column in which the element a_ij lies. Minor of an element a_ij is denoted by M_¡j.The order of minor matrix is (n -1).

8.Cofactor of an element a_ij denoted by A_ij is defined by

A_ij = (-1)^i+jM_ij, where M_ij is the minor of a_ij.

9.The adjoint of a square matrix A = [a_ij] is the transpose of the cofactor matrix [A_ij]_n×n-

10.A square matrix A is said to be singular if |A| = 0.

11.A square matrix A is said to be non-singular if |A| ≠ 0.

12.If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.

13.The determinant of the product of the matrices is equal to the product of the respective determinants, i.e., |AB| = |A||B|, where A and B are square matrices of the same order.

14.A square matrix A is invertible, i.e., its inverse exists if and only if A is a non-singular matrix. Inverse of matrix A (if it exists) is given by

15.A system of equations is said to be consistent if its solution (one or more) exists.

16.A system of equations is said to be inconsistent if its solution does not exist.

Notations to evaluate determinants:

i.R_i to denote the i^th row.

ii.R_i

\leftrightarrow

R_j to denote the interchange of the i^th and j^th rows.

iii.R_i

\leftrightarrow

R_j + λR_j to denote the addition of λ times the elements of the j^th row to the corresponding elements of the i^th row.

iv.R_i (λ) to denote the multiplication of all elements of the i^th row by λ.

v.Similar notations are used to denote column operations.

Top Concepts.

1.A determinant can be expanded along any of its rows (or columns). For easier calculations, it must be expanded along the row (or column) containing maximum zeroes.

2.Property 1: Value of the determinant remains unchanged if its rows and columns are interchanged. If A is a square matrix, then det(A) = det(A’), where A’ = transpose of A.

3.Property 2: If any two rows (or columns) of a determinant are identical, then the value of the determinant is zero.

4.Property 3: If A = [a_ij] is a square matrix of order n and B is the matrix obtained from A by multiplying each element of a row (or column) of A by a constant k, then its value gets multiplied by k. If

Δ_{1}

is the determinant obtained by applying R_i→kR_i or C_i→ kC_i to the determinant

Δ

, then

Δ_{1} = k Δ

. Thus, |B| = k|A|. This property enables removing the common factors from a given row or column.

5.If A is a square matrix of order n and k is a scalar, then |kA| = kⁿ |A|.

6.Property 4: If in a determinant, the elements in two rows or columns are proportional, then the value of the determinant is zero.

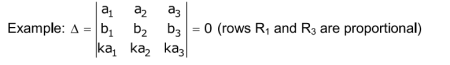
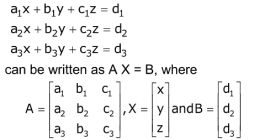
A picture containing text Description automatically generated

7.Property 5: If the elements of a row (or column) of a determinant are expressed as the sum of two terms, then the determinant can be expressed as the sum of the two determinants.

8.Property6: If to any row or column of a determinant, a multiple of another row or column is added, then the value of the determinant remains the same, i.e., the value of the determinant remains the same on applying the operation R_i

\to

R_i + kR_j or C_i

\to

C_i + kC_j.

9.Property 7: If any two rows (columns) of a determinant are interchanged, then the value of the determinant changes by a minus sign only.

10.Let A be a square matrix of order n(12) such that each element in a row (column) of A is zero, then |A|= 0.

11.If A – [a_ij] is a diagonal matrix of order n(

\geq

2) , then |A|a₁₁.a₂₂ a₃₃ … a_nn.

12.If A and B are square matrices of the same order, then |AB| = |A|.|B|

13.If more than one operation such as R_i

\to

R_i + kR_j is done in one step, care should be taken to see that a row which is affected in one operation should not be used in another operation. A similar remark applies to column operations.

14.Because area is a positive quantity, the absolute value of the determinant is taken in case of finding the area of a triangle.

15.If the area is given, then both positive and negative values of the determinant are used for calculation.

16.The area of a triangle formed by three collinear points is zero.

17.If A is a skew-symmetric matrix of odd order, then |A| = 0.

18.The determinant of a skew symmetric matrix of even order is a perfect square.

19.The minor of an element of a determinant of order n(n

\geq

2) is a determinant of order n-1.

20.The value of determinant of a matrix A is obtained by the sum of the product of the elements of a row (or column) with its corresponding cofactors. Example: |A| = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃ + A₁₃.

21.If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero.

22.Adjoint of a matrix: The adjoint of a square matrix A [a_ij]_{n × n} is defined as the transpose of the matrix [A_ij]_{n × n}, where A_ij is the cofactor of the element a_ij. Adjoint of the matrix A is denoted by adj A.

23.If A is any given square matrix of order n, then A (adj A) = (adj A) A = |A| I, where I is the identity matrix of order n.

24.A square matrix A is said to be singular if |A| = 0.

25.A square matrix is invertible if and only if A is a non-singular matrix.

26.The adjoint of a symmetric matrix is also a symmetric matrix.

27.If A is a non-singular matrix of order n, then |adj.A| = |A|^n-1.

28.If A and B are non-singular matrices of the same order, then AB and BA are also non-singular matrices of the same order.

29.If A is a non-singular square matrix, then adj(adj A) = |A|^n-2 A .

30.Determinants can be used to find the area of triangles whose vertices are given.

31.Determinants and matrices can also be used to solve the system of linear equations in two or three variables.

32.System of equations,

A picture containing text Description automatically generated

Then matrix X = A^-1 B gives the unique solution of the system of equations if |A| is non-zero and A^-1 exists.

Top Formulae

1.Area of a triangle with vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃)

2.Determinant of a matrix A = [a_ij]_{1 × 1} is given by |a₁₁|= a₁₁

Diagram Description automatically generated with medium confidence

4.Cofactor of a_ij is A_ij = (-1)^i+j. M_i.

6.If A and B are the square matrices of the same order, then |AB| = |A| |B|.

Logo Description automatically generated with medium confidence

8.If A and B are non-singular matrices of the same order, then

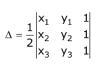
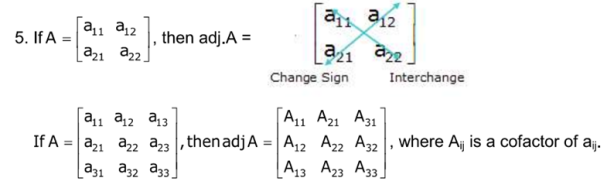
adj(AB) = (adj B)(adj A) .

9.If A is an invertible square matrix, then adj A^T-(adj A)^T.

10.Let A, B and C be square matrices of the same order n. If A is a non-singular matrix, then

11.If A and B are two invertible matrices of the same order, then (AB)^-1 =B^-1A^-1

12.If A, B and C are invertible matrices of the same order, then (ABC)^-1 = C^-1B^-1A^-1

13.If A is an invertible square matrix, then AT is also invertible and (AT)^-1 = (A^-1)^T

14.The inverse of an invertible symmetric matrix is a symmetric matrix.

15.If A is a non-singular matrix of order n, then adj (adj A) = |A|(^n-2)A

17.Cramer’s rule (system of two simultaneous equations with two unknowns): The solution of the system of simultaneous linear equations,

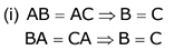
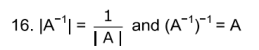
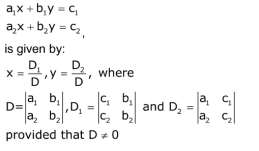
Text Description automatically generated with low confidence

18.Cramer’s rule (system of three simultaneous equations with three unknowns): The solution of the system of simultaneous linear equations,

19.For a system of two simultaneous linear equations with two unknowns:

i.If D ≠ 0, then the given system of equations is consistent and has a unique solution, given by

ii.If D = 0 and D₁ = D₂ = 0, then the system is consistent and has infinitely many solutions.

iii.If D = 0 and one of D₁ and D₂ is non-zero, then the system is inconsistent.

20.For a system of three simultaneous linear equations in three unknowns:

i.If D ≠ 0, then the given system of equations is consistent and has a unique solution given by

ii.If D = 0 and D₁ = D₂ = D₃ = 0, then the system is consistent and has infinitely many solutions.

21.Unique solution of equation AX = B is given by X = A^-1B, where |A| ≠ 0.

22.For a square matrix A in matrix equation AX = B,

i.If |A| ≠ 0, then there exists a unique solution.

ii.If |A| = 0 and (adj A) B ≠ 0, then there exists no solution.

iii.If |A| = 0 and (adj A) B = 0, then the system may or may not be consistent.

Important Questions

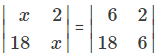Text Description automatically generated with low confidence Multiple Choice questions-

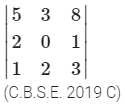
1. If , then x is equal to

(a) 6

(b) ±6

(d) 6, 6

2. Let A be a square matrix of order 3 × 3. Then |kA| is equal to

(a) k |A|

(b) k²|A|

(d) 3k|A|

3. Which of the following is correct?

(a) Determinant is a square matrix

(b) Determinant is a number associated to a matrix

(d) None of these.

4. If area of triangle is 35 sq. units with vertices (2, -6), (5, 4) and (k, 4). Then k is

(a) 12

(b) -2

Text Description automatically generated with low confidence (d) 12, -2.

5. If and A_ij is co-factors of a_ij, then A is given by

(a) a₁₁A₃₁ + a₁₂A₃₂ + a₁₃A₃₃

(b) a₁₁A₁₁ + a₁₂A₂₁ + a₁₃A₃₃

(d) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁

6. Let A be a non-singular matrix of order 3 × 3. Then |adj. A| is equal to

(a) |A|

(b) |A|²

(d) 3|A|

7. If A is any square matrix of order 3 x 3 such that |a| = 3, then the value of |adj. A| is?

(a) 3

(b) $\frac{1}{3}$

(d) 27

8. If A is an invertible matrix of order 2, then det (A-1) is equal to

(a) det (A)

(b) $\frac{1}{d e t (A)}$

(d) 0

9. If a, b, c are in A.P., then determinant

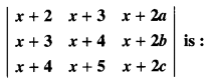
MCQ Questions for Class 12 Maths Chapter 4 Determinants with Answers 1

(a) 0

(b) 1

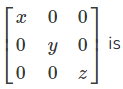Calendar Description automatically generated with medium confidence (d) 2x

10. If x, y, z are non-zero real numbers, then the inverse of matrix A =

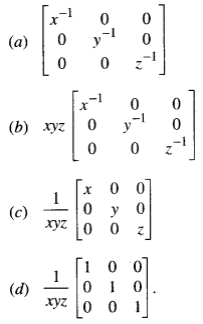
MCQ Questions for Class 12 Maths Chapter 4 Determinants with Answers 2

Very Short Questions:

1.Find the co-factor of the element a23 of the determinant:

Calendar Description automatically generated with low confidence

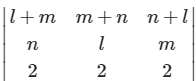A picture containing text, clock Description automatically generated

If A and B are invertible matrices of order 3, |A| = 2 and |(AB)^-1| = −

\frac{1}{6}

Find |B|. (C.B.S.E. Sample Paper 2018-19)

3.Check whether (l + m + n) is a factor of the determinant or not. Given reason. (C.B.S.E. Sample Paper 2020)

4.If A is a square matrix of order 3, with |A| = 9, then write the value of |2 . adj. A|. (A.I.C.B.S.E. 2019)

5.If A and B are square matrices of the same order 3, such that |A| = 2 and AB = 2I, write the value of IBI. (C.B.S.E. 2019)

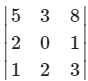Calendar Description automatically generated

A is a square matrix with |A| = 4. Then find the value of |A. (adj. A) |. (A.I.C.B.S.E. 2019)

7.If Δ = , write:

(i) the minor of the element a23 (C.B.S.E. 2012)

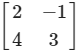A picture containing text, clock, watch Description automatically generated (ii) the co-factor of the element a32. (C.B.S.E. 2012)

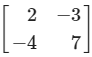Find the adjoint of the matrix A = (A.I.C.B.S.E. 2010)

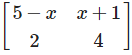Given A = compute A^-1 and show that 2A^-1 = 9I – A. (C.B.S.E. 2018)

10.For what value of ‘x’, the matrix is singular? (C.B.S.E. 2011)

Long Questions:

1.Using properties of determinants, prove the following:

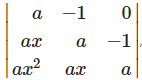
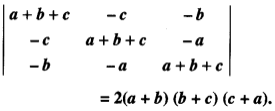
A picture containing text, clock Description automatically generated Class 12 Maths Important Questions Chapter 4 Determinants 5

2.If f(x) = ,using properties of determinants, find the value (C.B.S.E. 2015)

3.Using properties of determinants, prove that:

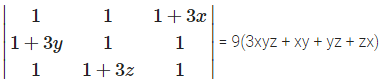
A picture containing text, clock Description automatically generated

4.Using properties of determinants, prove that:

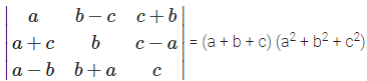
A picture containing schematic Description automatically generated

Assertion and Reason Questions-

1. Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes(a), (b), (c) and (d) as given below.

a)Both A and R are true and R is the correct explanation of A.

b)Both A and R are true but R is not the correct explanation of A.

c)A is true but R is false.

d)A is false and R is true.

e)Both A and R are false.

Assertion(A):Minor of element 6 in the matrix 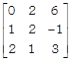A picture containing text, monitor, indoor, hand Description automatically generated is 3.

Reason (R):Minor of an element a_ij of a matrix is the determinant obtained by deleting its i^th

row.

2. Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes(a), (b), (c) and (d) as given below.

a)Both A and R are true and R is the correct explanation of A.

b)Both A and R are true but R is not the correct explanation of A.

c)A is true but R is false.

d)A is false and R is true.

e)Both A and R are false.

Assertion (A):For two matrices A and B of order 3, |A|=3, |B|=−4, then |2AB| is −96.

Reason(R):For a matrix A of order n and a scalar k, |kA|=kⁿ|A|.

Case Study Questions-

1.Raja purchases 3 pens, 2 pencils and 1 mathematics instrument box and pays ₹41 to the shopkeeper. His friends, Daya and Anil purchases 2 pens, 1 pencil, 2 instrument boxes and 2 pens, 2 pencils and 2 mathematical instrument boxes respectively. Daya and Anil pays ₹29 and ₹44 respectively. Based on the above information answer the following:

(i)The cost of one pen is:

a)₹2

b)₹5

c)₹10

d)₹15

(ii)The cost of one pen and one pencil is:

a)₹ 5

b)₹10

c)₹15

d)₹17

(iii)The cost of one pen and one mathematical instrument box is:

a)₹ 7

b)₹10

c)₹15

d)₹18

(iv)The cost of one pencil and one mathematical instrumental box is:

a)₹ 5

b)₹10

c)₹15

d)₹20

(v)The cost of one pen, one pencil and one mathematical instrumental box is:

a)₹ 10

b)₹15

c)₹22

d)₹25

2. The management committee of a residential colony decided to award some of its members (say x) for honesty, some (sayy) for helping others and some others (sayz) for supervising the workers to kept the colony neat and clean. The sum of all the awardees is 12. Three times the sum of awardees for cooperation and supervision added to two times the number of awardees for honesty is 33. The sum of the number of awardees for honesty and supervision is twice the number of awardees for helping.

A group of people shaking hands Description automatically generated

(i) Value of x + y + z is

(a) 3

(b) 5

(d) 12

(ii) Value of x − 2 y is

(a) z

(b) -z

(d) -2z

(iii) The value of z is

(a) 3

(b) 4

(d) 6

(iv) The value of x + 2 y is

(a) 9

(b) 10

(d) 12

(v) The value of 2x + 3y + 5z is

(a) 40

(b) 43

(d) 53

Answer Key-

Multiple Choice questions-

1.Answer: (a) 6

2.Answer: (c) k³|A|

3.Answer: (c) Determinant is a number associated to a square matrix

4.Answer: (d) 12, -2.

5.Answer: (d) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁

6.Answer: (b) |A|²

7.Answer: (c) 9

8.Answer: (b)

\frac{1}{d e t (A)}

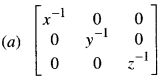MCQ Questions for Class 12 Maths Chapter 4 Determinants with Answers 3

Answer: (a) 0

10.Answer:

Very Short Answer:

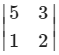Solution:

Co-factor of a₂₃ = (-1)^{2 + 3}

= (-1)⁵ (5 x 2 – 1 x 3)

= (-1) (10-3)

= (-1) (7) = -7.

2.Solution:

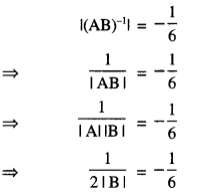
Class 12 Maths Important Questions Chapter 4 Determinants 1

Hence |B| = 3

3.Solution:

Given

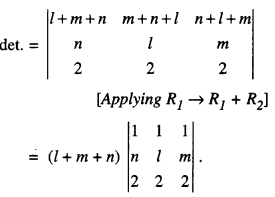
Class 12 Maths Important Questions Chapter 4 Determinants 3

Hence, (l + m + n) is a factor of given determinant.

4.Solution:

| 2 – adj. A| = 2³ | A |^3-1

= 8(9)²

= 648.

5.Solution:

We have: AB = 2I

∴ |AB| = |2I|

⇒ |A||B| = |2I|

⇒ 2|B|= 2(1).

Hence, |B| = 1.

6.Solution:

|A. (adj. A) | = |A|ⁿ

= 4ⁿ or 16 or 64.

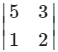Solution:

(i) a₂₃ =

= (5) (2) – (1) (3)

= 10 – 3 = 7.

(ii) a₃₂ = (-1)³⁺²

= (-1)⁵ [(5) (1) – (2) (8)]

= (-1)⁵ (5 – 16)

= (- 1) (- 11) = 11.

8.Solution:

Text Description automatically generated

Now A₁₁ = Co-factor of 2 = 3,

A₁₂ = Co-factor of – 1 = – 4,

A₂₁ = Co-factor of 4 = 1

and A₂₂ = Co-factor of 3 = 2

A picture containing text, clock Description automatically generated

9.Solution:

A picture containing text, clock Description automatically generated

= (2) (7) – (-4) (-3)

= 14 – 12 = 2 ≠ 0.

∴ A^-1 exists and

Text Description automatically generated with medium confidence

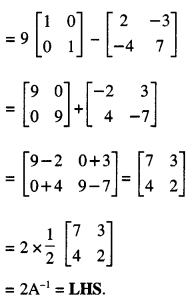
Class 12 Maths Important Questions Chapter 4 Determinants 4

10.Solution:

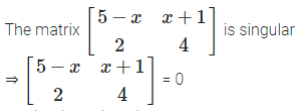
A screenshot of a computer Description automatically generated with low confidence

⇒ 4(5 -x) – 2 (x + 1) = 0

⇒ 20 – 4x – 2x – 2 = 0

⇒ 18 – 6x = 0

⇒ 6x = 18.

Hence, x = 3.

Long Answer:

1.Solution:

Class 12 Maths Important Questions Chapter 4 Determinants 6

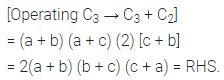
Text, letter Description automatically generated

2.Solution:

We have

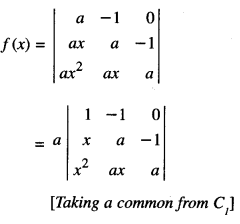
Class 12 Maths Important Questions Chapter 4 Determinants 7

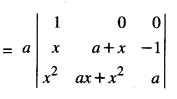
Class 12 Maths Important Questions Chapter 4 Determinants 8

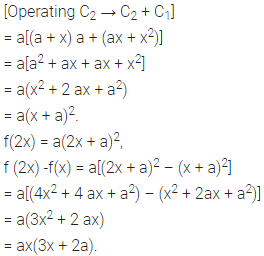
Text, letter Description automatically generated

3.Solution:

Class 12 Maths Important Questions Chapter 4 Determinants 9

(0 + 9yz) + 3x(3 z + 9yz + 3y)

= 9(3xyz + xy + yz + zx) = RHS

4.Solution:

Class 12 Maths Important Questions Chapter 4 Determinants 10

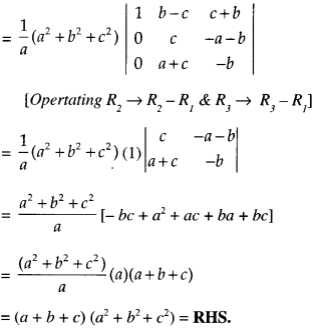
Class 12 Maths Important Questions Chapter 4 Determinants 11

Case Study Answers-

(i) (a) ₹ 2

(ii) (d) ₹ 17

(iii) (a) ₹ 7

(iv) (d) ₹20

(v) (c) ₹22

(i) (d) 12

(ii) (b)-z

(iii) (c)5

(iv) (c) 11

(v) (b)43

Assertion and Reason Answers-

1.(e)Both A and R are false.

Solution:

Minor of element

∴Given Assertion [A] is false Also we know that minor of an element a_ijof a matrix is the determinant obtained by deleting its i^throw and j^thcolumn.

∴ Given Reason (R) is also false

∴ Both Assertion [A] and Reason [R] are false Hence option (e) is the correct Answer.

2.(b) Both A and R are true but R is not the correct explanation of A.

Solution:

Here,

|2AB|=23|AB|=8|A||B|

=8×3×−4=−96

∴ Assertion [A] is true

{∵|kA|=kn|A|and|AB|=|A||B|}

Also we know that |kA|=kn|A|

for matrix A of order n.

∴ Reason (R) is true But |AB|=|A||B|is not mentioned in Reason R.