
constructions
Constructions
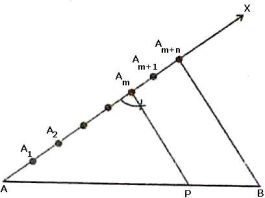
Step 1: Draw a line segment AB of given length by using a ruler.
Step 2: Draw any ray AX making an acute angle with AB.
Step 3: Along AX mark off (m + n) points A1, A2,………Am-1, Am+1,………,Am+n, such that AA1 = A1A2 = Am+n-1 Am+n.
Step 4: Join BAm+n
Step 5: Through the point Am, draw a line parallel to Am+nB by making an angle equal to ∠AAm+nB at Am, intersecting AB at point P.
The point P so obtained is the required point which divides AB internally in the ratio m: n.
 Justification
Justification
In ∆ABAm+n, we observe that Am P is parallel to Am+n B . Therefore, by Basic Proportionality theorem, we have:
AAmAmAm+n=APPB
=APPB=mn[∵AAmAmAm+n=mn, by construction]
=AP :PB = m : n
Hence, P divides AB in the ratio m: n.
Bisecting a Line Segment
Step 1: With a radius of more than half the length of the line segment, draw arcs centred at either end of the line segment so that they intersect on either side of the line segment.
Step 2: Join the points of intersection. The line segment is bisected by the line segment joining the points of intersection.
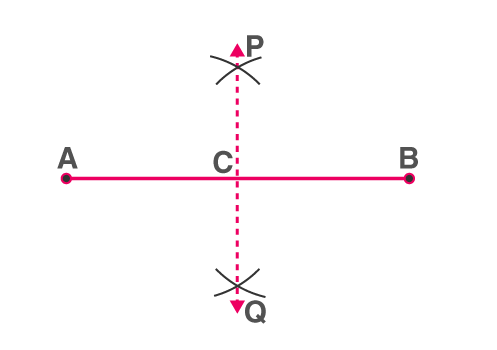
PQ is the perpendicular bisector of AB
 Example Find the point C such that it divides BA in ratio 2:3
Example Find the point C such that it divides BA in ratio 2:3
Steps of Construction:
Justification
Here ∆BB2C ̴ AA3C …AA test
BB2AA3=BCAC……(c.p.s.t.)
23=BCAC
Construction of Triangle Similar to given Triangle
Consider a triangle ABC. Let us construct a triangle similar to ∆ABC such that each of its sides is ||of (mn)th the corresponding sides of ABC.
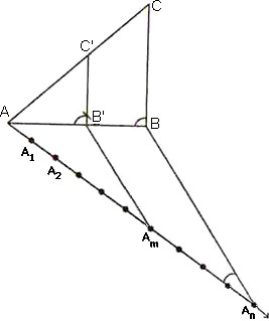
Steps of constructions when m < n:
Step 1: Construct the given triangle ABC by using the given data.
Step 2: Take any one of the three side of the given triangle as base. Let AB be the base of the given triangle.
Step 3: At one end, say A, of base AB. Construct an acute angle BAX below the base AB.
Step 4: Along AX mark off n points A1, A2, A3,………, An such that
AA1 = A1A2 = ……… = An-1 An
Step 5: Join AnB
Step 6: Draw AmB’ parallel to AnB which meets AB at B’.
Step 7: From B’ draw B’C’||BC meeting AC at C’.
Triangle AB’C’ is the required triangle each of whose sides is (mn)thof the corresponding side of ΔABC.
Justification
Since Am B’|| An B. Therefore
AB‘B‘B=AAmAmAn [by basic proportionality theorem]
AB‘B‘B=mn−m
B‘BAB‘=n−mm
Now, ABAB‘=AB‘+B‘BAB‘
ABAB‘=1+B‘BAB‘=1+n−mm+nm
AB‘AB=mn
In triangles ABC and AB’C’, we have
∠BAC = ∠B’ AC’
And ∠ABC = ∠AB’ C’
So, by AA similarity criterion, we have
∆AB’C’ ̴ ∆ABC
AB‘AB=B‘C‘BC=AC‘AC
AB‘AB=B‘C‘BC=AC‘AC=mn
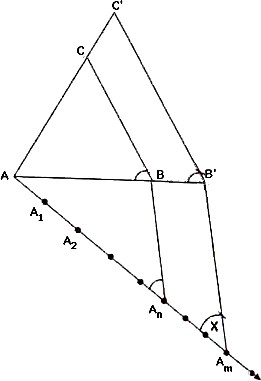
Steps of construction when m > n:
Step 1: Construct the given triangle by using the given data.
Step 2: Take any one of the three sides of the given triangle and consider it as the base. Let AB be the base of the given triangle.
Step 3: At one end, say A, of base AB. Construct an acute angle ∠BAX below base AB i.e., on the opposite side of the vertex C.
Step 4: Along AX mark off m (large of m and n) points A1, A2, A3,………Am of AX such that
AA1 = A1A2 = ………= Am-1Am.
Step 5: Join AnB to B and draw a line through Am parallel to AnB, intersecting the extended line segment AB at B’.
Step 6: Draw a line through B’ parallel to BC intersecting the extended line segment AC at C’. Step 7: ΔAB’C’ so obtained is the required triangle.
Justification
Consider triangle ABC and AB’ C’. We have:
∠BAC = ∠B‘ AC ‘
∠ABC = ∠AB ‘C ‘
So, by AA similarity criterion,
ΔABC ̴ ΔAB ‘C’
ABAB‘=BCB‘C‘=ACAC‘
ΔA Am B’, AnB || AmB’
∴ABBB‘=AAnAnAm
BB‘AB=AnAmAAn
BB‘AB=m−nn
AB‘−ABAB=m−nn
AB‘AB−1=m−nn
AB‘AB=mn
From (i) and (ii), we have
AB‘AB=B‘C‘BC=AC‘AC=mn
The tangent to a circle is a line that intersects the circle at exactly one point.
Tangent to a circle is perpendicular to the radius through the point of contact.
Construction of Triangle to a Circle from a point outside the Circle
Construction of a tangent to a circle from a point outside the circle, when its centre is known
The steps of constructions are as follows:
Step 1: Join the centre O of the circle to the point P.
Step 2: Draw perpendicular bisector of OP intersecting OP at Q.
Step 3: With Q as centre and radius OQ, draw a circle. This circle has OP as its diameter.
Step 4: Let this circle intersect the first circle at two points T and T’. Join PT and P T’ .
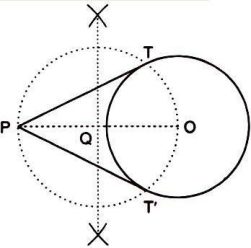 PT and P T’ are the two tangents to the given circle from the point P.
PT and P T’ are the two tangents to the given circle from the point P.
Justification
Join OT and OT’
It can be seen that ∠PTO is an angle in the semi-circle. We know that angle in a semi-circle is a right angle.
∴∠ PTO = 90°
OT ꓕ PT
Since OT is the radius of the circle, PT has to be a tangent of the circle. Similarly, PT’ is a tangent of the circle.
Number of Tangents to a circle from a given point
If the point is in an interior region of the circle, any line through that point will be a secant. So, in this case, there is no tangent to the circle.
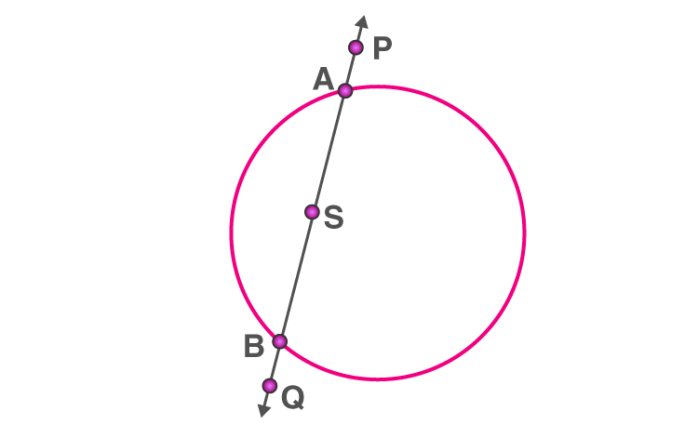
AB is a secant drawn through the point S
When the point lies on the circle, there is accurately only one tangent to a circle.
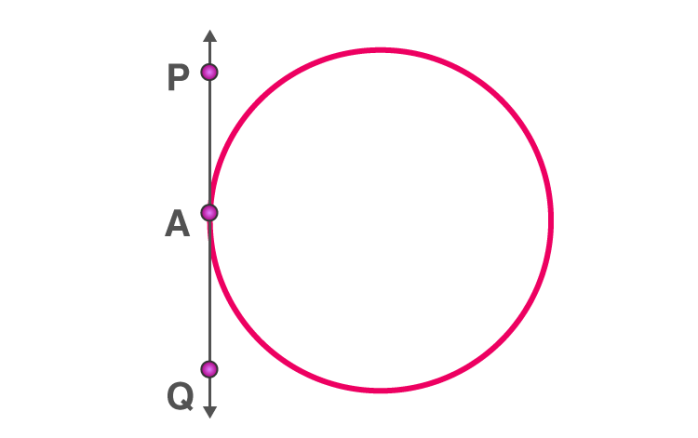
PQ is the tangent touching the circle at A
When the point lies outside of the circle, there are exactly two tangents to a circle.
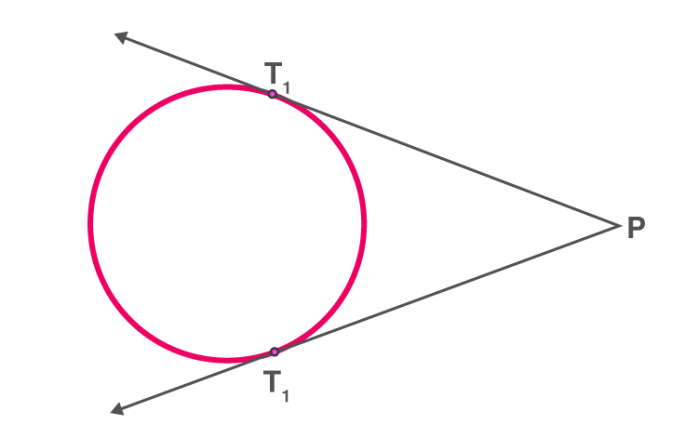
PT1 and PT2 are tangents touching the circle at T1 and T2
Drawing tangents to a circle from a point outside the circle
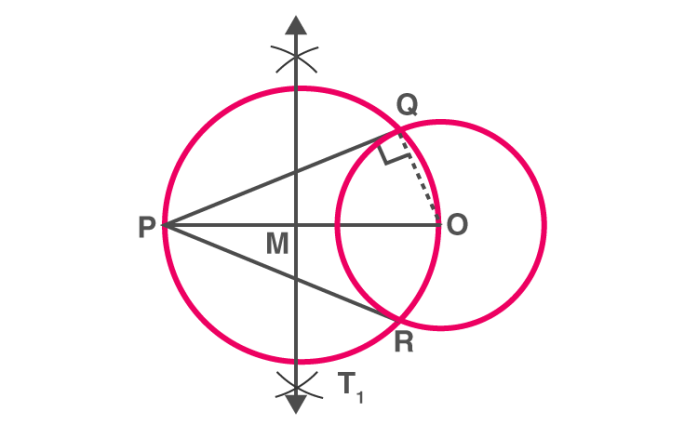
To construct the tangents to a circle from a point outside it.
Consider a circle with centre O and let P be the exterior point from which the tangents to be drawn.
Step 1: Join the PO and bisect it. Let M be the midpoint of PO.
Step 2: Taking M as the centre and MO(or MP) as radius, draw a circle. Let it intersect the given circle at the points Q and R.
Step 3: Join PQ and PR
Step 4:PQ and PR are the required tangents to the circle.
Important Questions
Multiple Choice questions-
1. To divide a line segment AB in the ratio p : q (p, q are positive integers), draw a ray AX so that ∠BAX is an acute angle and then mark points on ray AX at equal distances such that the minimum number of these points is
(a) greater of p and q
(b) p + q
(c) p + q – 1
(d) pq
2. To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is
(a) 105°
(b) 70°
(c) 140°
(d) 145°
3. To divide a line segment AB in the ratio 5 : 7, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is
(a) 8
(b) 10
(c) 11
(d) 12
4. To divide a line segment AB in the ratio 4 : 7, ray AX is drawn first such that ∠BAX is an acute angle and then points A1, A2, A3,……… are located at equal distances on the ray AX and the point B is joined to
(a) A12
(b) A11
(c) A10
(d) A9
5. To divide a line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray B4 parallel to AX and the points A1, A2, A3, …….. and B1, B2, B3,………. are located at equal distances on ray AX and B4, respectively. Then the points joined are:
(a) A5 and B6
(b) A6 and B5
(c) A4 and B5
(d) A5 and B4
6. To construct a triangle similar to a given ΔABC with its sides 37 of the corresponding sides of ΔABC, first draw a ray BX such that ∠CBX is an acute angle and X lies on the opposite side of A with respect to BC. Then locate points B1, B2, B3, on BX at equal distances and next step is to join
(a) B10 to C
(b) B3 to C
(c) B7 to C
(d) B4 to C
7. To construct a triangle similar to a given ΔABC with its sides 85 of the corresponding sides of ΔABC draw a ray BX such that ∠CBX is an acute angle and X is on the opposite side of A with respect to BC. Then minimum number of points to be located at equal distances on ray BX is
(a) 5
(b) 8
(c) 13
(d) 3
8. To draw a pair of tangents to a circle which are inclined to each other at an angle of 60°, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be:
(a) 135°
(b) 90°
(c) 60°
(d) 120°
9. To construct a pair of tangents to a circle at an angle of 60° to each other, it is needed to draw tangents at endpoints of those two radii of the circle, the angle between them should be:
(a) 100°
(b) 90°
(c) 180°
(d) 120°
10. A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of ___________ from the centre.
(a) 3.5 cm
(b) 2.5 cm
(c) 5 cm
(d) 2 cm
Very Short Questions:

Short Questions :
Long Questions :
Case Study Questions:
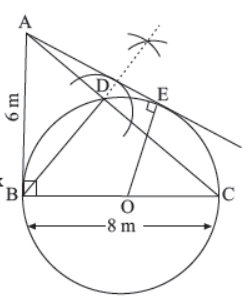
As it turns out, the road the engineer will be building and the road it will connect to both represent characteristics of a circle that have their own name. The road/bridge that already exists is called a secant of the circular lake, and the road the engineer is going to build is called the tangent of the circular lake.
Assertion Reason Questions-
Assertion: a, b and c are the lengths of three sides of a triangle, then a+b > c
Reason: The sum of two sides of a triangle is always greater than the third side.
Assertion: The side lengths 4cm, 4cm and 4cm can be sides of equilateral triangle.
Reason: Equilateral triangle has all its three sides equal.
Answer Key
Multiple Choice questions-
Very Short Answer :
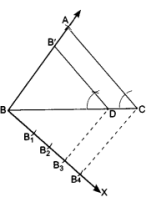
Given AB = 8 cm
AB’ = 34 of AB
= 34 × 8 = 6 cm
BB’ = AB – AB’ = 8 – 6 = 2 cm.
⇒ AB’: BB’ = 6 : 2 = 3 : 1
Hence the required ratio is 3 : 1.
Hence, PA : PB = 3 : 4
∴ AP : PB = 3 : 2
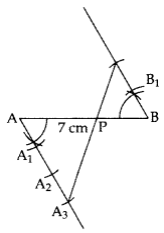
Hence, AP : AB = 3 : 5 or APAB=35
Short Answer :
AB = 5 cm
BC = 6 cm
∠ABC = 60°
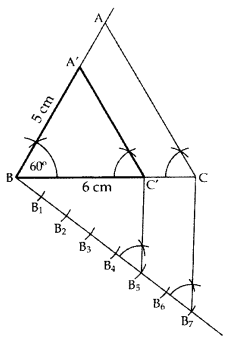
Hence, ∆A’BC’ is the required ∆.
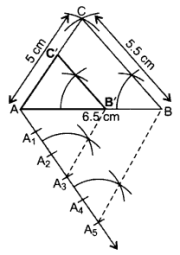
∴ ∆AB’C’ is the required ∆.
Ratio = 35 of corresponding sides
∴ ∆AB’C’ is the required triangle.
PQ = 5 cm, PR = 6 cm, ∠P = 120°
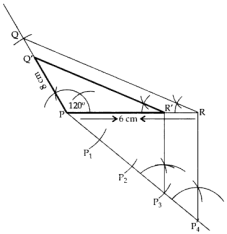
∴ ∆POʻR’ is the required ∆.
∴ ∆A’BC’ is the required triangle.
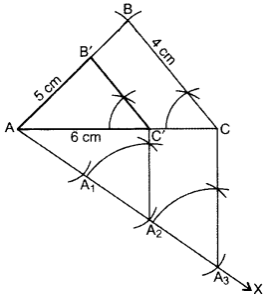
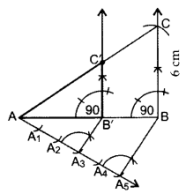
Steps of Construction:
Draw ∆ABC with AC = 6 cm, AB = 5 cm, BC = 4 cm.
Draw ray AX making an acute angle with AÇ.
Locate 3 equal points A1, A2, A3 on AX.
Join CA3.
Join A2C’ || CA3.
From point C’ draw B’C’ || BC.
∴ ∆AB’C’ is the required triangle.
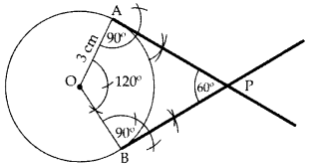
∴ PA & PB are the required tangents.+
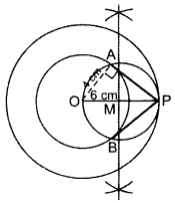
Steps of Construction:
Draw two circles with radius OA = 4 cm and OP = 6 cm with O as centre. Draw ⊥ bisector of OP at M. Taking M as centre and OM as radius draw another circle intersecting the smaller circle at A and B and touching the bigger circle at P. Join PA and PB. PA and PB are the required tangents.
Verification:
In rt. ∆OAP,
OA2 + AP2 = OP2 … [Pythagoras’ theorem
(4)2 + (AP)2 = (6)2
AP2 = 36 – 16 = 20
AP = +√20=√4×5
=2√5 2(2.236) = 4.472 = 4.5 cm
By measurement, ∴ PA = PB = 4.5 cm
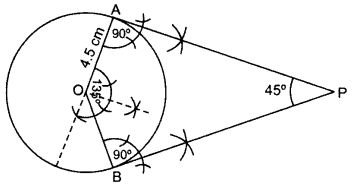
Draw ∠AOB = 135°, ∠OAP = 90°, ∠OBP = 90°
∴ PA and PB are the required tangents.
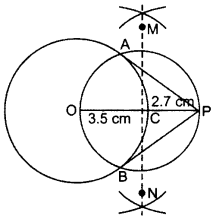
Hence AP & PB are the required tangents.
Long Answer :
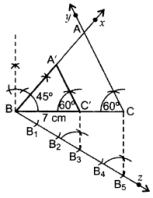
105° + 45° + C = 180°
∠C = 180° – 105° – 45o = 30°
BC = 7 cm
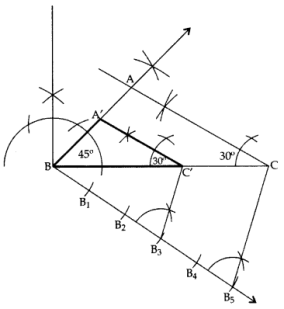
∴ ∆A’BC’ is the required ∆.
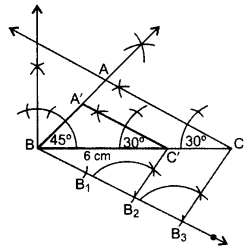
In ∆ABC,
∠A + ∠B + ∠C = 180° …[Angle-sum-property of a ∆
105° + ∠B + 30° = 180°
∠B = 180° – 105° – 30° = 45°
∴ ∆A’BC’ is the required ∆.
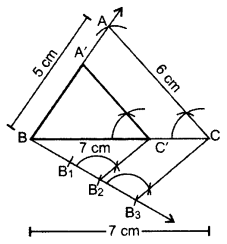
∴ ∆A’BC’ is the required triangle.
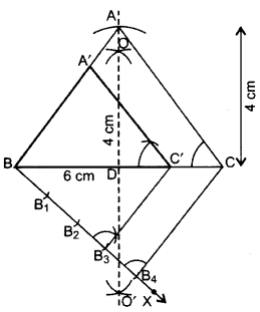
∴ ∆A’BC’ is the required triangle.
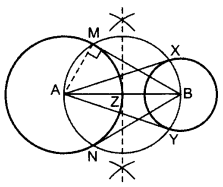
Step of constructions:
Draw two circles on A and B as asked.
Z is the mid-point of AB.
From Z, draw a circle taking ZA = ZB as radius,
so that the circle intersects the bigger circle at M and N and smaller circle at X and Y.
Join AX and AY, BM and BN.
BM, BN are the required tangents from external point B.
AX, AY are the required tangents from external point A.
Justification:
∠AMB = 90° …[Angle in a semi-circle
Since, AM is a radius of the given circle.
∴BM is a tangent to the circle
Similarly, BN, AX and AY are also tangents.
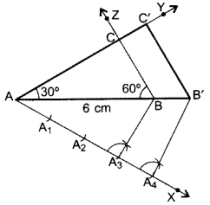
Steps of construction:
Hence, ∆AB’C’ is the required triangle.
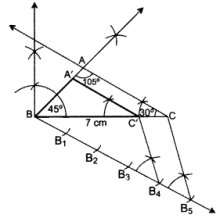
∴ ∆A’BC’ is the required ∆.
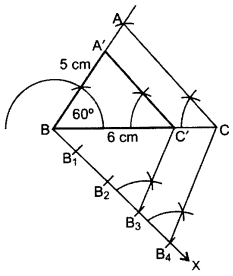
Steps of Construction:
Then ∆AB’C’ in the required triangle.
Justification:

Case Study Answer:
Assertion Reason Answer-
(a) Both A and R are true and R is the correct explanation of A.
(a) Both A and R are true and R is the correct explanation of A.






