
Circles
Circles
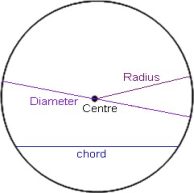
A circle is the locus of a point which lies in the plane in such a manner that its distance from a fixed point in the plane is constant. The fixed point is called the centre and the constant distance is called the radius of the circle.
Circle and line in a plane
For a circle and a line on a plane, there can be three possibilities.
they can be non-intersecting
they can have a single common point: in this case, the line touches the circle.
they can have two common points: in this case, the line cuts the circle.
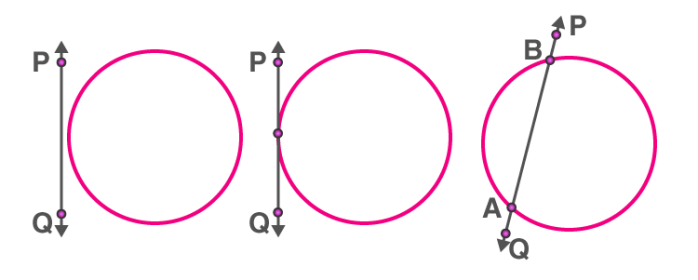
(i) Non intersecting (ii) Touching (iii) Intersecting
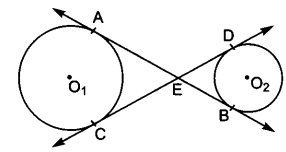
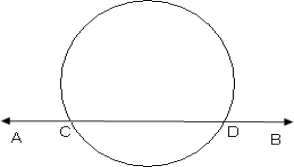 In the figure, AB is a secant to the circle.
In the figure, AB is a secant to the circle.
A tangent to the circle is a line that intersects the circle (touches the circle) at only one point. The word ’tangent’ comes from the Latin word ‘tangere’, which means to touch. The common point of the circle and the tangent is called point of contact.
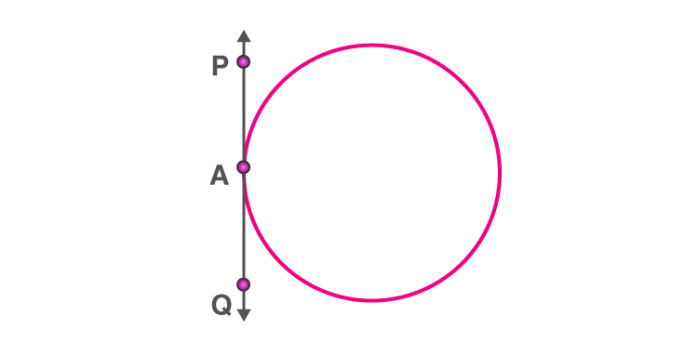 In the figure, AB is a tangent to the circle and P is the point of contact.
In the figure, AB is a tangent to the circle and P is the point of contact.
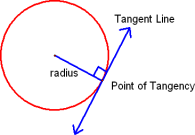
The length of the segment of the tangent from the external point P and the point of contact with the circle is called the length of the tangent.
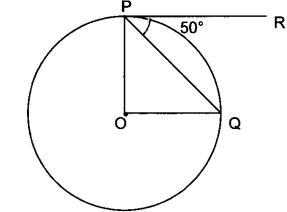
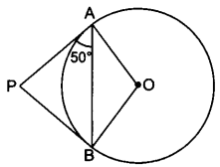
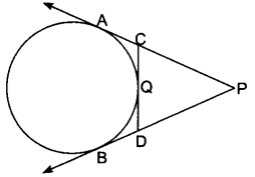
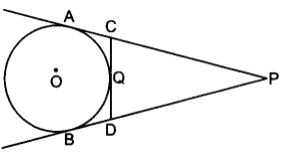
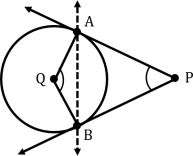 Angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.In the figure, angle P and angle Q are supplementary.
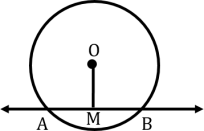
Perpendicular drawn from the centre to any chord of the circle, divides it into two equal parts. In the figure, OM is perpendicular to AB and AM = MB.
 The line containing the radius through the point of contact is called the normal to the circle at that point.
The line containing the radius through the point of contact is called the normal to the circle at that point.
Opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
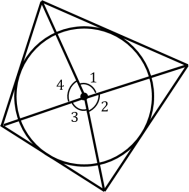
In the figure, angles 1 and 3 are supplementary. Accordingly, angles 2 and 4 are supplementary.
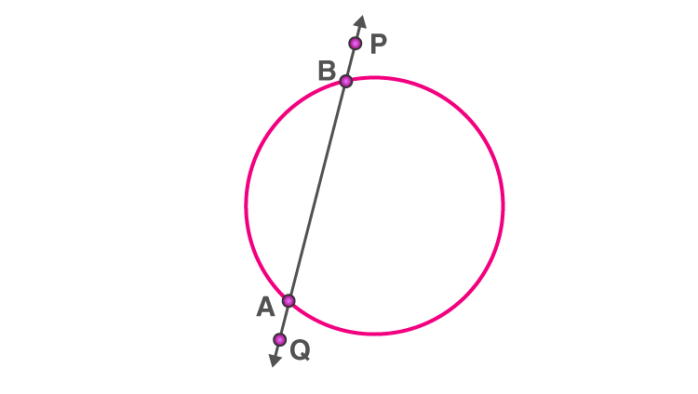
Secant
A secant to a circle is a line that has two points in common with the circle. It cuts the circle at two points, forming a chord of the circle.
Tangent as a special case of Secant
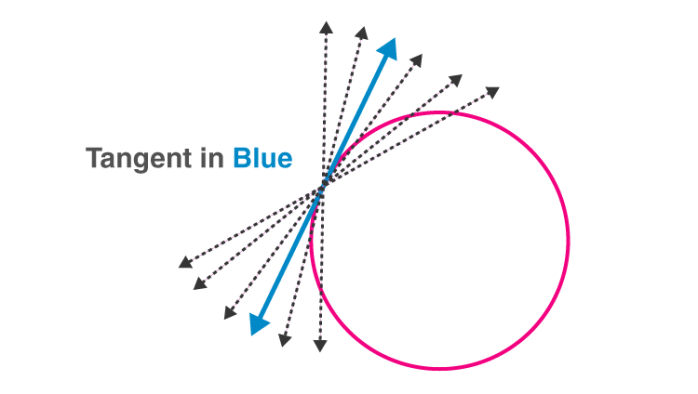
The tangent to a circle can be seen as a special case of the secant when the two endpoints of its corresponding chord coincide.
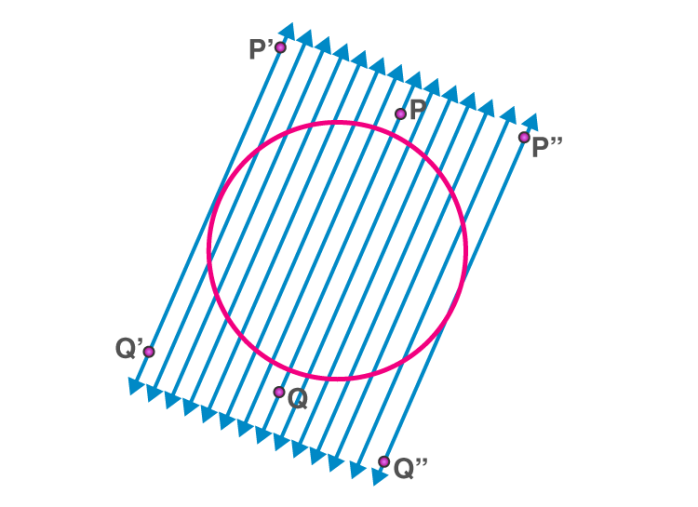
Two parallel tangents at most for a given secant
For every given secant of a circle, there are exactly two tangents which are parallel to it and touches the circle at two diametrically opposite points.
Theorems
Tangent perpendicular to the radius at the point of contact
Theorem: The theorem states that “the tangent to the circle at any point is the perpendicular to the radius of the circle that passes through the point of contact”.
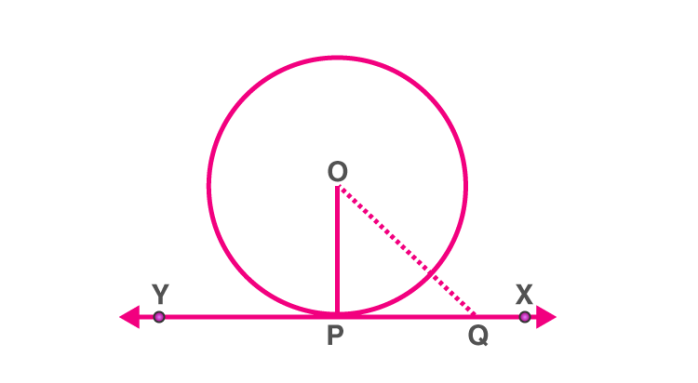
Here, O is the centre and OP⊥XY.
The number of tangents drawn from a given point
If the point is in an interior region of the circle, any line through that point will be a secant. So, no tangent can be drawn to a circle which passes through a point that lies inside it.
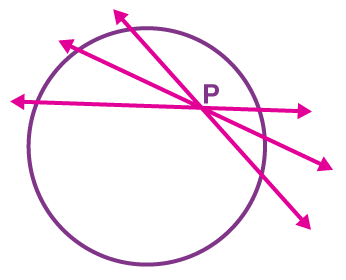
No tangent can be drawn to a circle from a point inside it
AB is a secant drawn through the point S
When a point of tangency lies on the circle, there is exactly one tangent to a circle that passes through it.
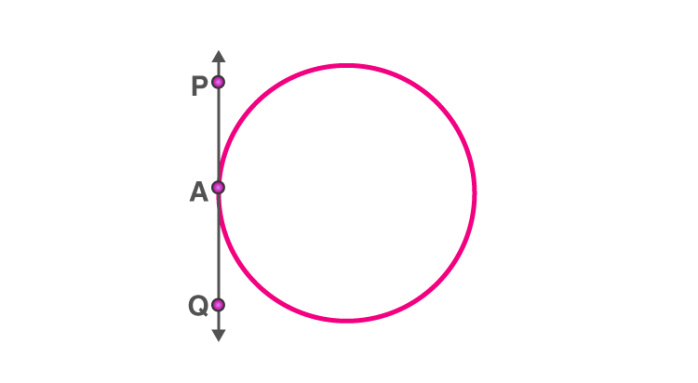
A tangent passing through a point lying on the circle
When the point lies outside of the circle, there are accurately two tangents to a circle through it
Tangents to a circle from an external point
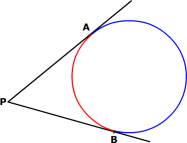
Length of a tangent
The length of the tangent from the point (Say P) to the circle is defined as the segment of the tangent from the external point P to the point of tangency I with the circle. In this case, PI is the tangent length.

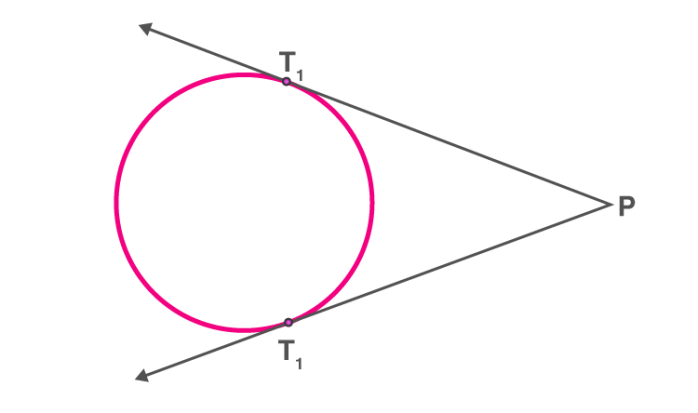
Lengths of tangents drawn from an external point
Theorem: Two tangents are of equal length when the tangent is drawn from an external point to a circle.

PT1 = PT2
Thus, the two important theorems in Class 10 Maths Chapter 10 Circles are:
Theorem 10.1: The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Theorem 10.2: The lengths of tangents drawn from an external point to a circle are equal.
Interesting facts about Circles and its properties are listed below:
In two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
The tangents drawn at the ends of a diameter of a circle are parallel.
The perpendicular at the point of contact to the tangent to a circle passes through the centre.
The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
The parallelogram circumscribing a circle is a rhombus.
The opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Important Questions
Multiple Choice questions-
1. Two circle touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB =
(a) 60°
(b) 45°
(c) 30°
(d) 90°
2. If TP and TQ are two tangents to a circle with centre O so that ∠POQ = 110°, then, ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°
3. Tangents from an external point to a circle are
(a) equal
(b) not equal
(c) parallel
(d) perpendicular
4. Two parallel lines touch the circle at points A and B respectively. If area of the circle is 25 n cm2, then AB is equal to
(a) 5 cm
(b) 8 cm
(c) 10 cm
(d) 25 cm
5. A line through point of contact and passing through centre of circle is known as
(a) tangent
(b) chord
(c) normal
(d) segment
6. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q
(a) √119 cm
(b) 13 cm
(c) 12 cm
(d) 8.5 cm
7. From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(a) 60 cm2
(b) 65 cm2
(c) 30 cm2
(d) 32.5 cm2
8. At point A on a diameter AB of a circle of radius 10 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY at a distance 16 cm from A is
(a) 8 cm
(b) 10 cm
(c) 16 cm
(d) 18 cm
9. The tangents drawn at the extremities of the diameter of a circle are
(a) perpendicular
(b) parallel
(c) equal
(d) none of these
10. A circle is inscribed in a ΔABC having AB = 10cm, BC = 12cm and CA = 8cm and touching these sides at D, E, F respectively. The lengths of AD, BE and CF will be
(a) AD = 4cm, BE = 6cm, CF = 8cm
(b) AD = 5cm, BE = 9cm, CF = 4cm
(c) AD = 3cm, BE = 7cm, CF = 5cm
(d) AD = 2cm, BE = 6cm, CF = 7cm
Very Short Questions:
Short Questions :
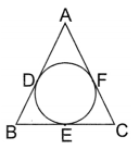
OR
In Fig. if AB = AC, prove that BE = EC.
[Note: D, E, F replace by F, D, E]
Long Questions :
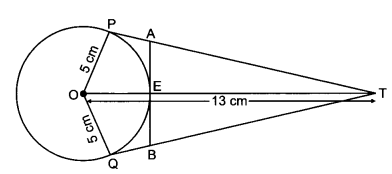
Case Study Questions:
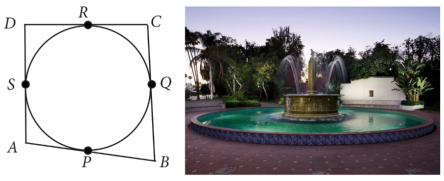
Based on the above information, answer the following questions.

Assertion Reason Questions-
Assertion (A): In a circle of radius 6 cm, the angle of a sector is 60°. Then the area of the sector is 132/7 cm2.
Reason (R): Area of the circle with radius r is πr2
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference 2π× radius.
Answer Key-
Multiple Choice questions-
Very Short Answer :
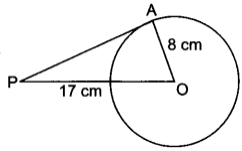
OA ⊥ PA (∵ radius is ⊥ to tangent at point of contact)
∴ In ∆OAP, we have
PO2 = PA2 + AO2
⇒ (17)2 = (PA)2 + (8)2
(PA)2 = 289 – 64 = 225
⇒ PA = √225 = 15
Hence, the length of the tangent from point P is 15 cm.
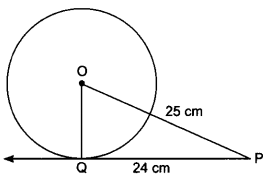
∵ OQ ⊥ PQ
∴ PQ2 + QO2 = OP2
⇒ 252 = OQ2 + 242
or OQ = √625 – √576
= √49 = 7 cm
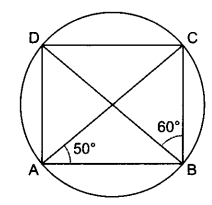
In ABCD, we have
∠BCD = 180° – (∠BDC + ∠DBC)
= 180° – (50° + 60°)= 70°
∴ ∠COD = 115°
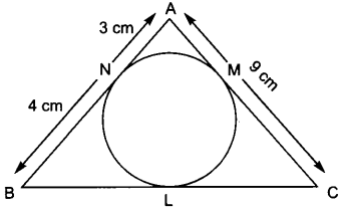
BN = BL = 4 cm [Tangents drawn from an external point]
CL = CM = AC – AM = 9 – 3 = 6 cm
⇒ BC = BL + CL = 4 + 6 = 10 cm.
OP = OQ [Radii of a circle]
∠OPQ = ∠OQP = 40°
(Equal opposite sides have equal opposite angles)
∠POQ = 180° – ∠OPQ – ∠OQP
= 180° – 40° – 40° = 100°
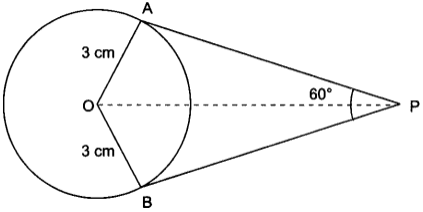
∆AOP ≅ ∆BOP (By SSS congruence criterion)
∠APO = ∠BPO = 60°2 = 30°
In ∆AOP, OA ⊥ AP
∴ tan 30° = OAAP
⇒ 1√3 = 3AP
⇒ AP = 3√3 cm
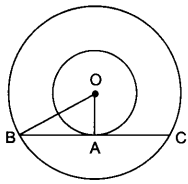
OA = 4 cm, OB = 5 cm
Also, OA ⊥ BC
∴ OB2 = OA2 + AB2
⇒ 52 = 42 + AB2
⇒ AB = √25 – √16 = 3 cm
⇒ BC = 2 AB = 2 × 3 = 6 cm
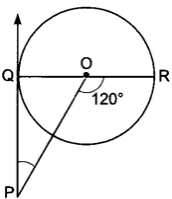
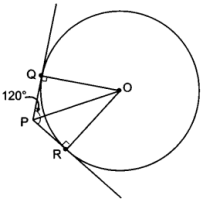
∠OQP = 90°
∠QOP = 180° – 120° = 60°
∠OPQ = 180° – ∠OQP – ∠QOP
= 180° – 90° – 60°
= 30°
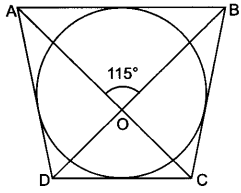
∴ ∠APB = 180° – 50° – 50° = 80°
∴ ∠AOB = 180° – 80° = 100°
Short Answer :

True, Join OC,
∠ACB = 90° (Angle in semi-circle)
∴ ∠OBC = 180o – (90° + 30°) = 60°
Since, OB = OC = radii of same circle [Fig. 8.16]
∴ ∠OBC = ∠OCB = 60°
Also, ∠OCD = 90°
⇒ ∠BCD = 90° – 60° = 30°
Now, ∠OBC = ∠BCD + ∠BDC (Exterior angle property)
⇒ 60° = 30° + ∠BDC
⇒ ∠BDC = 30°
∵ ∠BCD = ∠BDC = 30°
∴ BC = BD
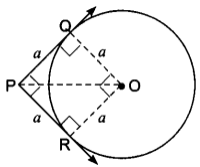
Then ∆PQO is always a right angled triangle with OP as the hypotenuse. So, PQ is always less than OP.
Since ∠P = 90°, so ∠QOR = 90°
Also, OR = OQ = a
∴ PQOR is a square
![]()
∴ PA = PB = 15 cm
Now, Perimeter of ∆PCD = PC + CD + DP = PC + CQ + QD + DP
= PC + CA + DB + DP
= PA + PB = 15 + 15 = 30 cm
⇒ 12 = PC + 3 = PC = 9 cm
∵ PA = PB = PA – AC = PB – BD
⇒ PC = PD
∴ PD = 9 cm
Hence, PC + PD = 18 cm
Construction : Join OB and OY.
Draw OP||AC
Since AB||PO
∠ABO + ∠POB = 180° (Adjacent interior angles)
∠ABO = 90° (A tangent to a circle is perpendicular to the radius through the point of contact)
90° + ∠POB = 180° = ∠POB = 90°
Similarly ∠POY = 90°
∠POB + ∠POY = 90° + 90° = 180°
Hence, BOY is a straight line passing through the centre of the circle.
Radius is perpendicular to the tangent at the point of contact.
∠OQP = 90°
⇒ ∠QPO = 60°
(Tangents drawn to a circle from an external point are equally inclined to the segment, joining the centre to that point)
![]()
2PQ = PO
On addition, we get
AE + BE = CE + ED
∠QPO = 60°
⇒ AB = CD
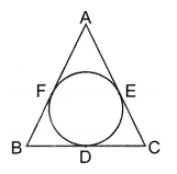
Given, AB = AC
We have, BF + AF = AE + CE ….(i)
AB, BC and CA are tangents to the circle at F, D and E respectively.
∴ BF = BD, AE = AF and CE = CD ….(ii)
From (i) and (ii)
BD + AE = AE + CD (∵ AF = AE)
⇒ BD = CD
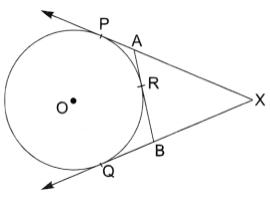
AP = AR
BR = BQ
XP = XQ [Tangent to a circle from an external point are equal]
XA + AP = XB + BQ
XA + AR = XB + BR [AP = AR, BQ = BR]
Long Answer :
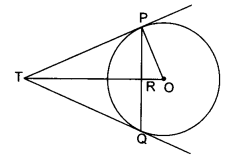
To Prove: OP ⊥ AB.
Construction: Take any point l, other than P, on the tangent AB. Join OQ. Suppose OQ meets the circle at R.
Proof: We know that among all line segments joining the point to a point on AB, the shortest one is perpendicular to AB. So, to prove that OP ⊥ AB it is sufficient to prove that OP is shorter than any other segment joining O to any point of AB.
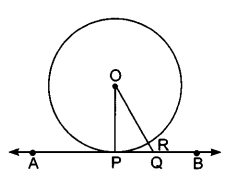
Clearly, OP = OR [Radii of the same circle]
Now, OQ = OR + RQ
⇒ OQ > OR
⇒ OQ > OP [∵OP = OR]
Thus, OP is shorter than any other segment joining O to any point on AB.
Hence, OP ⊥ AB.
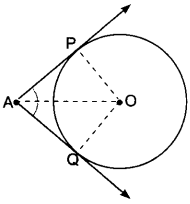
Given: AP and AQ are two tangents from a point A to a circle C (O, r).
To Prove: AP = AQ
Construction: Join OP, OQ and OA.
Proof: In order to prove that AP = AQ, we shall first prove that ∆OPA ≅ ∆OQA.
Since a tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OP ⊥ AP and OQ ⊥ AQ
⇒ ∠OPA = ∠OQA = 90°
Now, in right triangles OPA and OQA, we have
OP = OQ [Radii of a circle]
∠OPA = ∠OQA [Each 90°]
and OA = OA [Common]
So, by RHS-criterion of congruence, we get
∆OPA ≅ OQA
⇒ AP = AQ [CPCT]
Hence, lengths of two tangents from an external point are equal.
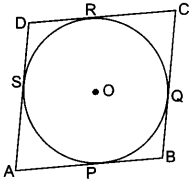
Let ABCD be a parallelogram such that its sides touch a circle with centre O.
We know that the tangents to a circle from an exterior point are equal in length.
Therefore, we have
AP = AS [Tangents from A]
BP = BQ [Tangents from B] …. (ii)
CR = CQ [Tangents from C] …. (iii)
And DR = DS [Tangents from D] …. (iv)
Adding (i), (ii), (iii) and (iv), we have
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC [∵ ABCD is a parallelogram ∴ AB = CD, BC = DA]
2AB = 2BC ⇒ AB = BC
Thus, AB = BC = CD = AD
Hence, ABCD is a rhombus.


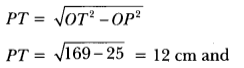
TE = 8 cm
Let PA = AE = x
(Tangents from an external point to a circle are equal)
In right ∆AET
TA2 = TE2 + EA2
⇒ (12 – x)2 = 64 + x2
⇒ 144 + x2 – 24x = 64 + x2
⇒ x = 8024
⇒ x = 3.3 cm
Thus, AB = 6.6 cm
Case Study Answer:
Solution:
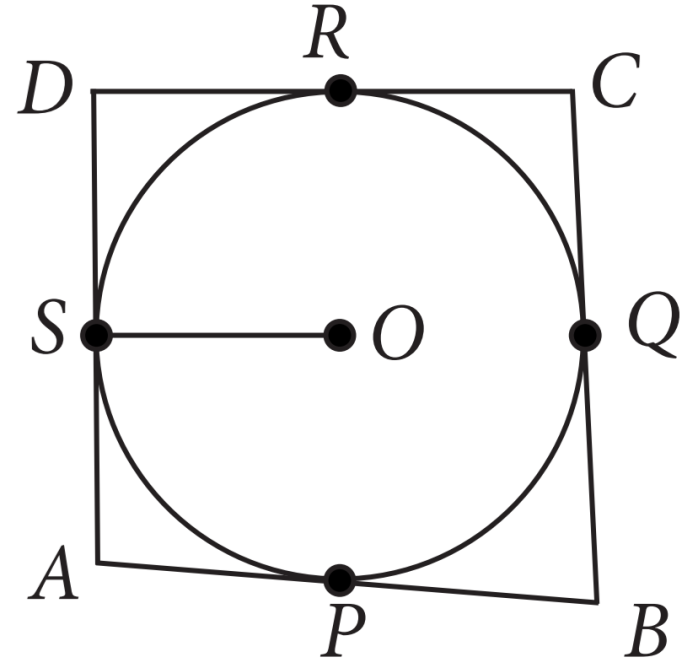
Here, OS the is radius of circle.
Since radius at the point of contact is perpendicular to tangent So, ∠OSA=90o
Solution:
Since, length of tangents drawn from an external point to a circle are equal.
∴ AS = AP, BP = BQ,
CQ = CR and DR = DS
Solution:
AP = AS = AD – DS = AD – DR = 11 – 7 = 4cm.
Solution:
In quadrilateral OQCR,
∠QCR = 60o, (Given)
And ∠OQC = ∠ORC = 90o
[Since, radius at the point of contact is perpendicular to tangent.]
∴ ∠QCR = 360o − 90o − 90o − 60o = 120
Solution:
From (I), we have AS = AP, DS = DR, BQ = BP and CQ = CR
Adding all above equations, we get
AS + DS + BQ + CQ = AP + DR + BP + CR
⇒ AD + BC = AB + CD
Assertion Reason Answer-






