Arithmetic Progressions

∴ (k + 10) – 2k = (3k + 2) – (k + 10)

⇒ -k + 10 = 2k – 8 or 3k = 18 or k = 6.

Let d be the common difference

d = a_n+1 – an

= 5 – 11(n + 1) – (5 – 11n)

= 5 – 11n – 11 -5 + 11n = -11

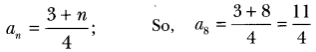
∴ second term – First term = Third term – second term

⇒ 13 – (2p + 1) = 5p – 3 – 13

⇒ 13 – 2p – 1 = 5p – 16

⇒ 12 – 2p = 5p – 16

⇒ -7p = – 28

⇒ p = 4

Putting the values given, we get

⇒ 4 = a + (7 – 1)(-4) or a = 4 + 24

⇒ a = 28

We know,

a₂₅ = a + (25 – 1 )d

= (-5) + $24\left(\frac{5}{2}\right)$ = -5 + 60 = 55

⇒ (a + 17d) – (a + 13d) = 32

⇒ 17d – 13d = 32 or d $=\frac{32}{4}$

Here 200 -150 = 250 – 200 = 300 – 250 and so on

∴ It forms a_n AP with a = 150, d = 50

(ii) The numbers involved are 10,800, 11,600, 12,400, …

which forms an AP with a = 10,800 and d = 800.

And, common difference d = 2nd term – 1st term = 8 – 3 = 5

Therefore, 20^th term from end = 1 -(20 – 1) × d = 253 – 19 × 5 = 253 – 95 = 158.

= ap² + bp – (ap² + a – 2ap + bp – b)

= ap² + bp – ap² – a + 2ap – bp + b = 2ap + b-a .

= a₁ = 2a + b – a = a + b and a₂ = 4a + b – a = 3a + b

⇒ d = a₂ – a₁ = (3a + b) – (a + b) = 2a

Given, a = 5, T_n = 45, s_n = 400 .

Tn = a + (m – 1)d

⇒ 45 = 5 + (m – 1)d

⇒ (n – 1) d = 40 ………(i)

s_n = $\frac{n}{2}$ (a + T_n)  

⇒ 400 = $\frac{n}{2}$ (5 + 45)

⇒ n = 2 × 8 = 16 substituting the value of n in (i)

⇒ (16 – 1)d = 40

⇒ d = $\frac{40}{15}$ = $\frac{8}{3}$

so, a1 = 110, d = 10, a_n = 990

We know, a_n = a₁ + (n – 1)d

990 = 110 + (n – 1) 10

(n – 1) = $\frac{990-110}{10}$

⇒ n = 88 + 1 = 89

3, 8, 13, 18, …..

Here, a = 3, d = 8 – 3 = 5 and a_n = 78

Now, a_n = a + (n – 1)d

⇒ 78 = 3 + (n – 1) 5

⇒ 78 – 3 = (n – 1) × 5

⇒ 75 = (n – 1) × 5

⇒ $\frac{75}{5}$ = n – 1

⇒ 15 = n – 1

⇒ n = 15 + 1 = 16

Hence, 16^th term of given AP is 78.

Now, we have

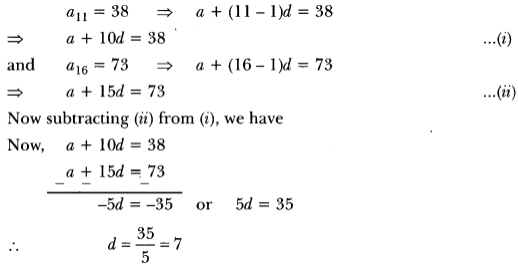
Putting the value of d in equation (i), we have

a + 10 × 7 = 38

⇒ a + 70 = 38

⇒ a = 38 – 70

⇒ a = – 32

We have, a = -32 and d = 7

Therefore, a₃₁ = a + (31 – 1)d

⇒ a₃₁ = a + 30d

⇒ (-32) + 30 × 7

⇒ – 32 + 210

= a₃₁ = 178

since, given AP consists of 50 terms, so n = 50

a₃ = 12

⇒ a + 2d = 12 …(i)

Also, a₅₀ = 106

⇒ a + 490 = 106 … (ii)

subtracting (i) from (ii), we have

47d = 94

⇒ d = $\frac{94}{47}$ = 2

Putting the value of d in equation (i), we have

a + 2 × 2 = 12

⇒ a = 12 – 4 = 8

Here, a = 8, d = 2

∴ 29th term is given by

a₂₉ = a + (29 – 1)d = 8 + 28 × 2

⇒ a₂₉ = 8 + 56

⇒ a₂₉ = 64

We have, a₈ = 31 and a15 = 16 + a₁₁

⇒ a + 7d = 31 and a + 14d = 16 + a + 10d

⇒ a + 7d = 31 and 4d = 16

⇒ a + 7d = 31 and d = 4

⇒ a + 7 × 4 = 31

⇒ a + 28 = 31

⇒ a= 3

Hence, the AP is a, a + d, a + 2d, a + 3d…..

i.e., 3, 7, 11, 15, 19, …

∴ a₃₁ = a + 30d = 5 + 30 × 10 = 305

Let nth term of the given AP be 130 more than its 31^st term. Then,

a_n = 130 + a₃₁

∴ a + (n – 1)d = 130 + 305

⇒ 5 + 10(n – 1) = 435

⇒ 10(n – 1) = 430

⇒ n – 1 = 43

⇒ n = 44

Hence, 44^th term of the given AP is 130 more than its 31^st term.

⇒ a + (4 – 1)d + a + (8 – 1) d = 24

⇒ 2a + 3d + 7d = 24

⇒ 2a + 10d = 24

⇒ 2(a + 5d) = 24

∴ a + 5d = 12

and, a₆ + a₁₀ = 44

⇒ a + (6 – 1)d + a + (10 – 1) d = 44

⇒ 2a + 5d + 9d = 44

⇒ 2a + 14d = 44

⇒ a + 7d = 22

subtracting (i) from (ii), we have

2d = 10

$\therefore d=\frac{10}{2}=5$

Putting the value of d in equation (i), we have

a + 5 × 5 = 12

⇒ a = 12 – 25 = -13

Here, a = -13, d = 5

Hence, first three terms are

-13, -13, + 5, -13 + 2 × 5 i.e., -13, -8, -3

Replacing n by (n – 1), we get

s_n-1 = 3(n – 1)² – 4(n – 1) ….(ii)

We know, .

a_n = s_n – s_n-1 = {3n² – 4n} – {3(n – 1)² – 4(n – 1)}.

= {3n² – 4n} – {3n² + 3 – 6n – 4n + 4}

= 3n² – 4n – 3n² – 3 + 6n + 4n – 4 = 6n – 7

so, nth term an = 6n – 7

To get the AP, substituting n = 1, 2, 3… respectively in (iii), we get

a₁ = 6 × 1-7 = -1,

a₂ = 6 × 2 – 7 = 5

a₃ = 6 × 3 – 7 = 11,…

Hence, AP is – 1,5, 1:1, …

Also, to get 12th term, substituting n = 12 in (iii), we get

a₁₂ = 6 × 12 – 7 = 72 – 7 = 65

Given, (a – 3d) + (a – d) + (a + d) + (a + 3d) = 56

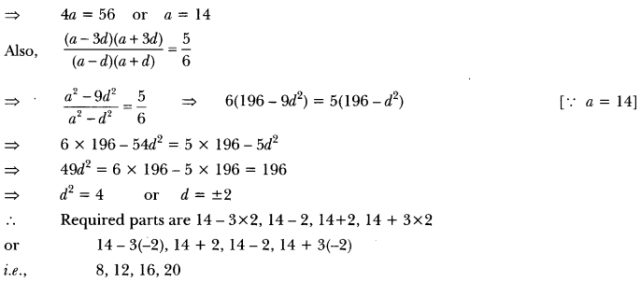
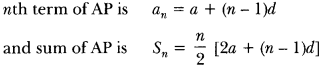
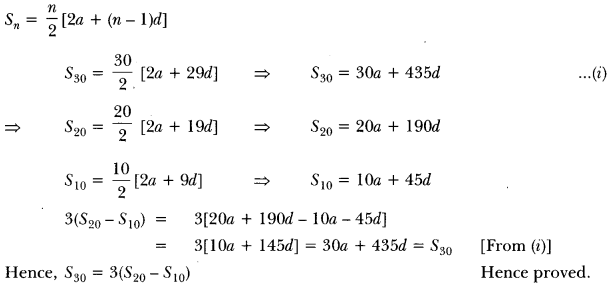
Total distance covered by thief = 100 n metres

Total distance covered by policeman = 100 + 110 + 120 + … + (n – 1) terms

∴ 100m = $\frac{n-1}{2}$ [100(2) + (n – 2)10]

⇒ 200n = (n – 1)(180 + 10n)

⇒ 102– 30n – 180 = 0

⇒ n2 – 3n – 18 = 0

⇒ (n-6) (n + 3) = 0

⇒ n = 6

Policeman took (n – 1) = (6 – 1) = 5 minutes to catch the thief.

The numbers of the houses are in AP, where a = 1 and d = 1

sum of n terms of an AP = $\frac{n}{2}$[2a + (n – 1)d]

Let X^th number house be the required house.

sum of number of houses preceding X^th house is equal to sx-1 i.e.,

since number of houses is positive integer,

∴ X = 35

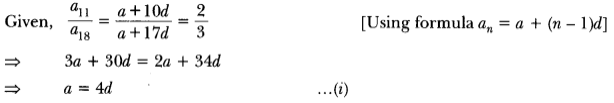
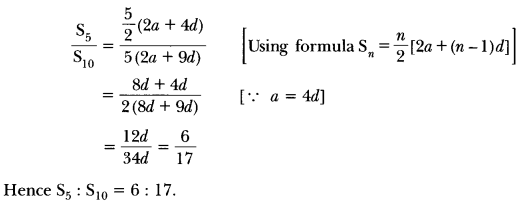
8, 16, 24, … 120

Clearly, these numbers are in AP with first term a = 8 and common difference, d = 16 – 8 = 8

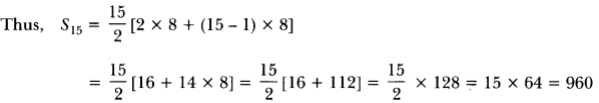
10, 13, 16, 19, …, 97, which forms an AP.

with a = 10, d = 3, an = 97

an = 97 = a + (n – 1) d = 97

or 10 + (n – 1)3 = 97

⇒ (n – 1) = $\frac{87}{3}$ = 29

⇒ n = 30

Now, s₃₀ = [2 × 10 + 29 × 3) = 15(20 + 87) = 15 × 107 = 1605

Here the smallest 3-digit number divisible by 7 is 105. So, the number of bacteria taken into consideration is 105, 112, 119, …. 994 So, first term (a) = 105, d = 7 and last term = 994.

Solution:

t₅ = a + 4d = 105 + 28 = 133

Solution:

Let n samples be taken under consideration  

∵ Last term = 994

⇒ a + (n – d)d = 994

⇒ 105 + (n – 1)7 = 994

⇒ n = 128

Solution:

Total number of bacteria in first 10 samples

Solution:

t₇ from end = (128 – 7 + 1) term from beginning = 122^th term = 105 + 121(7) = 952

Solution:

t₅₀ = 105 + 49 × 7 = 448

Geeta’s A.P. is -5, -2, 1, 4, … Here, first term (a₁) = -5 and conunon difference (d₁) = -2 + 5 = 3 Similarly, Madhuri’s A.P. is 187, 184, 181, … Here first term (a₂) = 187 and common difference (d₂) = 184 – 187 = -3

Solution:

t₃₄ = a₂ + 33d₂ = 187 + 33(-3) = 88

Solution:

Required sum = 3 + (-3) = 0

Solution:

t₁₉ = a₁ + 18d₁ = (-5) + 18(3) = 49

Solution:

Solution:

Let n^th terms of the two A.P s be equal.

∵ -5 + (n – 1)3 = 187 + (n – 1)(-3)

⇒ 6(n – 1) = 192

⇒ n = 33

Assertion Reason Answer-