https://makemynotes.in/arithmetic-progressions/

Arithmetic Progressions

1.What is a Sequence?

A sequence is an arrangement of numbers in a definite order according to some rule.

The various numbers occurring in a sequence are called its terms.

We denote the terms of a sequence by a₁, a₂, a₃…etc. Here, the subscripts denote the positions of the terms in the sequence.

In general, the number at the n^th place is called the n^th term of the sequence and is denoted by an. The n^th term is also called the general term of the sequence.

A sequence having a finite number of terms is called a finite sequence.

A sequence which do not have a last term and which extends indefinitely is known as an infinite sequence.

Sequences, Series and Progressions

A sequence is a finite or infinite list of numbers following a specific pattern. For example, 1, 2, 3, 4, 5,… is the sequence, an infinite sequence of natural numbers.

A series is the sum of the elements in the corresponding sequence. For example, 1 + 2 + 3 + 4 + 5….is the series of natural numbers. Each number in a sequence or a series is called a term.

A progression is a sequence in which the general term can be can be expressed using a mathematical formula.

2.Arithmetic Progression:

An arithmetic progression is a list of numbers in which each term is obtained by adding a fixed number to the preceding term, except the first term.

Each of the numbers of the sequence is called a term of an Arithmetic Progression. The fixed number is called the common difference. This common difference could be a positive number, a negative number or even zero.

3.General form and general term (n^th term) of an A.P:

The general form of an A.P. is a, a + d, a + 2d, a + 3d….., where ‘a’ is the first term and ‘d’ is the common difference.

The general term (n^th term) of an A.P is given by an = a + (n – 1) d, where ‘a’ is the first term and ‘d’ is the common difference.

If the A.P a, a + d, a + 2d, …….., l is reversed to l, l – d, l – 2d, ….., a then the common difference changes to negative of the common difference of the original sequence.

To find the n^th term from the end, we consider this AP backward such that the last term becomes the first term.

l, (l – d), (l – 2d) ……

The general term of this AP is given by a_n = + (n – 1)(-d)

4.Algorithm to determine whether a sequence is an AP or not:

When we are given an algebraic formula for the general term of the sequence:

Step 1: Obtain a_n.

Step 2: Replace n by (n + 1) in an to get a_n+1

Step 3: Calculate a_n+1 – a_n

Step 4: Check the value of a_n+1 – a_n.

If a_n+1 – a_n is independent of n, then the given sequence is an A.P. Otherwise, it is not an A.P.

A list of numbers a₁, a₂, a₃…… is an A.P, if the differences a₂ – a₁, a₃ – a₂, a₄ – a₃ … give the same value, i.e., a_k+1 – a_k is same for all different values of k.

5.Sometimes we require certain number of terms in A.P. The following ways of selecting terms are generally very convenient.

Number of terms	Terms	Common difference
3	a – d, a, a + d	d
4	a – 3d, a – d, a + d, a + 3d	2d
5	a – 2d, a – d, a, a + d, a + 2d	d
6	a – 5d, a – 3d, a – d, a + d, a + 3d, a + 5d	2d

It should be noted that in case of an odd number of terms, the middle term is ‘a’ and the common difference is ‘d’ while in case of an even number of terms the middle terms are a – d, a + d and the common differences is 2d.

6.Arithmetic mean:

If three number a, b, c (in order) are in A.P. Then,

b – a = c – b = common difference

⇒ 2b = a + c

Thus a, b and c are in A.P., if and only if 2b = a + c. In this case, b is called the Arithmetic mean of a and c.

7.Sum of n terms of an A.P:

Sum of n terms of an A.P. is given by:

$S_{n} = \frac{n}{2} [2 a + (n - 1) d]$

where ‘a’ is the first term, ‘d’ is the common difference and ‘n’ is the total number of terms.

Sum of n terms of an A.P. is also given by:

$S_{n} = \frac{n}{2} [a + l]$

where ‘a’ is the first term and ‘ $λ$ ’ is the last term.

Sum of first n natural numbers is given by

\frac{n (n + 1)}{2}

8.The n^th term of an A.P is the difference of the sum to first n terms and the sum to first (n – 1) terms of it. That is, a_n = S_n – S_n-1

9.Common Difference

The difference between two consecutive terms in an AP, (which is constant) is the “common difference“(d) of an A.P. In the progression: 2, 5, 8, 11, 14 …the common difference is 3.

As it is the difference between any two consecutive terms, for any A.P, if the common difference is:

• positive, the AP is increasing.

• zero, the AP is constant.

• negative, the A.P is decreasing.

10.Finite and Infinite AP

• A finite AP is an A.P in which the number of terms is finite. For example the A.P: 2, 5, 8……32, 35, 38

• An infinite A.P is an A.P in which the number of terms is infinite. For example: 2, 5, 8, 11…..

A finite A.P will have the last term, whereas an infinite A.P won’t.

Finite sets are the sets having a finite/countable number of members. Finite sets are also known as countable sets as they can be counted. The process will run out of elements to list if the elements of this set have a finite number of members.

Examples of finite sets:

P = {0, 3, 6, 9, …, 99}

Q = {a : a is an integer, 1 < a < 10}

A set of all English Alphabets (because it is countable).

Another example of a Finite set:

A set of months in a year.

M = {January, February, March, April, May, June, July, August, September, October, November, December}

n (M) = 12

It is a finite set because the number of elements is countable.

Cardinality of Finite Set

If ‘a’ represents the number of elements of set A, then the cardinality of a finite set is n(A) = a.

So, the Cardinality of the set A of all English Alphabets is 26, because the number of elements (alphabets) is 26.

Hence, n (A) = 26.

Similarly, for a set containing the months in a year will have a cardinality of 12.

So, this way we can list all the elements of any finite set and list them in the curly braces or in Roster form.

Properties of Finite sets

The following finite set conditions are always finite.

• A subset of Finite set

• The union of two finite sets

• The power set of a finite set

Few Examples:

P = {1, 2, 3, 4}

Q = {2, 4, 6, 8}

R = {2, 3)

Here, all the P, Q, R are the finite sets because the elements are finite and countable.

$\begin{matrix} . \subset \end{matrix}$

P, i.e R is a Subset of P because all the elements of set R are present in P. So, the subset of a finite set is always finite.

P U Q is {1, 2, 3, 4, 6, 8}, so the union of two sets is also finite.

The number of elements of a power set = 2ⁿ.

The number of elements of the power set of set P is 24 = 16, as the number of elements of set P is 4. So it shows that the power set of a finite set is finite.

Non- Empty Finite set

It is a set where either the number of elements are big or only starting or ending is given. So, we denote it with the number of elements with n(A) and if n(A)is a natural number then it’s a finite set.

Example:

S = {a set of the number of people living in India}

It is difficult to calculate the number of people living in India but it’s somewhere a natural number. So, we can call it a non-empty finite set.

If N is a set of natural numbers less than n. So the cardinality of set N is n.

N = {1,2,3….n}

X = x₁, x₂, ……, x_n

Y = {x : x₁ ϵ N, 1 ≤ i ≤ n}, where i is the integer between 1 and n.

Can we say that an empty set is a finite set?

Let’s learn what is an empty set first.

An empty set is a set which has no elements in it and can be represented as { } and shows that it has no element.

P = { } Or ∅

As the finite set has a countable number of elements and the empty set has zero elements so, it is a definite number of elements.

So, with a cardinality of zero, an empty set is a finite set.

What is Infinite set?

If a set is not finite, it is called an infinite set because the number of elements in that set is not countable and also we cannot represent it in Roster form. Thus, infinite sets are also known as uncountable sets.

So, the elements of an Infinite set are represented by 3 dots (ellipse) thus, it represents the infinity of that set.

Examples of Infinite Sets

• A set of all whole numbers, W = {0, 1, 2, 3, 4,…}

• A set of all points on a line

• The set of all integers

Cardinality of Infinite Sets

The cardinality of a set is n (A) = x, where x is the number of elements of a set A. The cardinality of an infinite set is n (A) = ∞ as the number of elements is unlimited in it.

Properties of Infinite Sets

• The union of two infinite sets is infinite

• The power set of an infinite set is infinite

• The superset of an infinite set is also infinite

11.Comparison of Finite and Infinite Sets

Let’s compare the differences between Finite and Infinite set:

The sets could be equal only if their elements are the same, so a set could be equal only if it is a finite set, whereas if the elements are not comparable, the set is infinite.

Factors	Finite sets	Infinite sets
Number of elements	Elements are countable	The number of elements is uncountable
Continuity	It has a start and end elements	It is endless from the start or end. Both the sides could have continuity
Cardinality	n(A) = n, n is the number of elements in the set	n(A) = ∞ as the number of elements are uncountable
union	Union of two finite sets is finite	Union of two infinite sets is infinite
Power set	The power set of a finite set is also finite	The power set of an infinite set is infinite
Roster form	Can be easily represented in roster form	As the set in infinite set can’t be represented in Roster form, so we use three dots to represent the infinity

How to know if a Set is Finite or Infinite?

As we know that if a set has a starting point and an ending point both, it is a finite set, but it is infinite if it has no end from any side or both sides.

Points to identify a set is whether a finite or infinite are:

An infinite set is endless from the start or end, but both the side could have continuity unlike in Finite set where both start and end elements are there.

If a set has the unlimited number of elements, then it is infinite and if the elements are countable then it is finite.

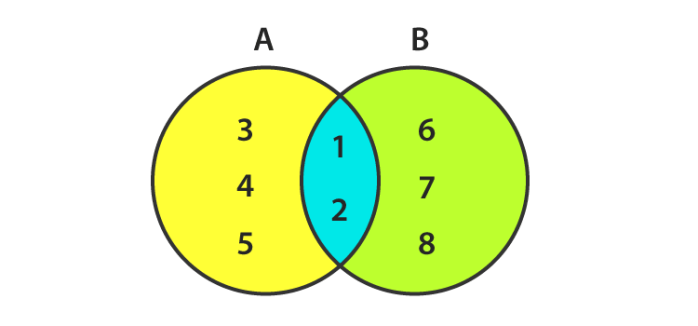
12.Graphical Representation of Finite and Infinite Sets

Here in the above picture,

A = {1, 2, 3, 4, 5}

B = {1, 2, 6, 7, 8}

A U B = {1, 2, 3, 4, 5, 6, 7, 8}

A∩B = {1, 2}

Both A and B are finite sets as they have a limited number of elements.

n(A) = 5 and n(B) = 5

AUB and A∩B are also finite.

So, a Venn diagram can represent the finite set but it is difficult to do the same for an infinite set as the number of elements can’t be counted and bounced in a circle

Important Questions

Multiple Choice questions-

1. The n^th term of an A.P. is given by an = 3 + 4n. The common difference is

(a) 7

(b) 3

(d) 1

2. If p, q, r and s are in A.P. then r – q is

(a) s – p

(b) s – q

(d) none of these

3. If the sum of three numbers in an A.P. is 9 and their product is 24, then numbers are

(a) 2, 4, 6

(b) 1, 5, 3

(d) 2, 3, 4

4. The (n – 1)^th term of an A.P. is given by 7,12,17, 22,… is

(a) 5n + 2

(b) 5n + 3

(d) 5n – 3

5. The n^th term of an A.P. 5, 2, -1, -4, -7 … is

(a) 2n + 5

(b) 2n – 5

(d) 3n – 8

6. The 10th term from the end of the A.P. -5, -10, –15,…, -1000 is

(a) -955

(b) -945

(d) -965

7. Find the sum of 12 terms of an A.P. whose nth term is given by an = 3n + 4

(a) 262

(b) 272

(d) 292

8. The sum of all two digit odd numbers is

(a) 2575

(b) 2475

(d) 2425

9. The sum of first n odd natural numbers is

(a) 2n²

(b) 2n + 1

(d) n²

10. The number of multiples lie between n and n² which are divisible by n is

(a) n + 1

(b) n

(d) n – 2

Very Short Questions:

1.Which of the following can be the n^th term of a_n AP?

4n + 3, 3n² + 5, n² + 1 give reason.

2.Is 144 a term of the AP: 3, 7, 11, …? Justify your answer.

3.The first term of a_n AP is p and its common difference is q. Find its 10^th term.

4.For what value of k: 2k, k + 10 and 3k + 2 are in AP?

5.If a_n = 5 – 11n, find the common difference.

6.If n^th term of an AP is

\frac{3 + n}{4}

find its 8^th term.

7.For what value of p are 2p + 1, 13, 5p – 3, three consecutive terms of AP?

8.In a_n AP, if d = -4, n = 7, a, = 4 then find a.

9.Find the 25^th term of the AP: –

5, \frac{- 5}{2}

0, \frac{- 5}{2}

10.Find the common difference of an AP in which a₁₈ – a₁₄ = 32.

Short Questions :

1.In which of the following situations, does the list of numbers involved to make an AP? If yes, give a reason.

(i) The cost of digging a well after every meter of digging, when it costs 150 for the first meter and rises by 50 for each subsequent meter.

(ii) The amount of money in the account every year, when 10,000 is deposited at simple interest at 8% per annum.

2.Find the 20^th term from the last term of the AP: 3, 8, 13, …, 253.

3.If the sum of the first p terms of an AP is ap² + bp, find its common difference.

4.The first and the last terms of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.

5.Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.

6.Which term of the AP: 3, 8, 13, 18, … , is 78?

7.Find the 31^st term of an AP whose 11^th term is 38 and the 16^th term is 73.

8.An AP consists of 50 terms of which 3^rd term is 12 and the last term is 106. Find the 29^th term.

9.If the 8^th term of an AP is 31 and the 15^th term is 16 more than the 11^th term, find the AP.

10.Which term of the arithmetic progression 5, 15, 25, …. will be 130 more than its 31^st term?

Long Questions :

1.The sum of the 4^th and 8^th term of an AP is 24 and the sum of the 6^th and 10^th term is 44. Find the first three terms of the AP.

2.The sum of the first n terms of an AP is given by sn = 3n² – 4n. Determine the AP and the 12^th term.

3.Divide 56 into four parts which are in AP such that the ratio of product of extremes to the product of means is 5 : 6.

4.In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the AP.

5.If s, denotes the sum of the first n terms of an AP, prove that s₃₀ = 3 (s₂₀ – s₁₀).

6.A thief runs with a uniform speed of 100 m/minute. After one minute a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief?

7.The houses in a row are numbered consecutively from 1 to 49. show that there exists a value of X such that sum of numbers of houses preceeding the house numbered X is equal to sum of the numbers of houses following X. Find value of X.

8.If the ratio of the 11^th term of an AP to its 18^th term is 2:3, find the ratio of the sum of the first five terms to the sum of its first 10 terms.

9.Find the sum of the first 15 multiples of 8.

10.Find the sum of all two digit natural numbers which when divided by 3 yield 1 as remainder.

Case Study Questions:

1.ln a pathology lab, a culture test has been conducted. ln the test, the number of bacteria taken into consideration in various samples is all 3-digit numbers that are divisible by 7, taken in order.

A person working on a computer Description automatically generated with low confidence

On the basis of above information, answer the following questions

i.How many bacteria are considered in the fifth sample?

a.126

b.140

c.133

d.149

ii.How many samples should be taken into consideration?

a.129

b.128

c.130

d.127

iii.Find the total number of bacteria in the first 10 samples.

a.1365

b.1335

c.1302

d.1540

iv.How many bacteria are there in the 7^th sample from the last?

a.952

b.945

c.959

d.966

v.The number of bacteria in 50^th sample is?

a.546

b.553

c.448

d.496

2.ln a class the teacher asks every student to write an example of A.P. Two friends Geeta and Madhuri writes their progressions as -5, -2, 1, 4,….. and 187, 184, 181, …. respectively. Now, the teacher asks various students of the class the following questions on these two progressions. Help students to find the answers of the questions.

Children sitting at a table Description automatically generated with low confidence

i.Find the 34^thterm of the progression written by Madhuri.

a.86

b.88

c.-99

d.190

ii.Find the sum of common difference of the two progressions.

a.6

b.-6

c.1

d.0

iii.Find the 19^th tenn of the progression written by Geeta.

a.49

b.59

c.52

d.62

iv.Find the sum of first 10 terms of the progression written by Geeta.

a.85

b.95

c.110

d.200

v.Which term of the two progressions will have the same value?

a.31

b.33

c.32

d.30

Assertion Reason Questions-

1.Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

a.Both A and R are true and R is the correct explanation for A.

b.Both A and R are true and R is the correct explanation for A.

c.A is true but R is false.

d.A is false but R is true.

Assertion: 184 is the 50^th term of the sequence 3, 7, 11, …………

Reason: The nth term of A.P. is given by a_n = a + (n – 1)d

2.Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

a.Both A and R are true and R is the correct explanation for A.

b.Both A and R are true and R is the correct explanation for A.

c.A is true but R is false.

d.A is false but R is true.

Assertion: The nth term of A.P. is given by a_n = a + (n – 1)d

Reason: Common difference of the A.P. a, a + d, a + 2d, …….., is given by d = 2^nd term – 1^st term.

Pages: 1 2

Leave a Reply Cancel reply

Related Stories

Constructions

Probability

Statistics

You may have missed

বিজ্ঞানের জয়যাত্রা ও মানুষের ভবিষ্যৎ-Bigyaner jayayatra o manuser bhabisyat

বাংলার ঋতুচক্র-Banglar Rituchakra

প্রিয় গ্রন্থকার -“মানিক বন্দ্যোপাধ্যায়”-Priya granthakar- Manik bandyopadhay

তোমার প্রিয় কবি (জীবনানন্দ দাস )-Tomar priya kabi (Jibanananda das)