
Areas Related to Circles
Answer Key-
Multiple Choice questions-
Very Short Answer :
∴ p2 = side2 + side2
⇒ p2 = 2side2
or side2 = p22 cm2 = area of the square
![]()
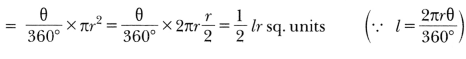
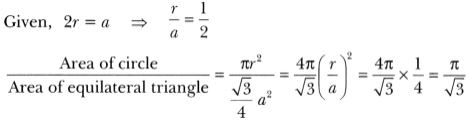
∴ Its area = d
Diagonal of inner square = d
∴ Side = d√2
⇒ Area = d22
Area of outer square = 2 × Area of inner square.
⇒ 2r = r2
⇒ r(r – 2) = 0 or r = 2
i.e. d = 4 units
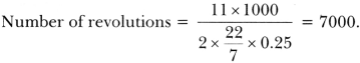
= (2r + πr) cm
⇒ 2r + πr = 36
⇒ r(2+227)= 36
⇒ r = 7cm
Diameter 2r = 2 × 7 = 14 cm.
= 227 × 7 + 2 × 7 = 22 + 14 = 36cm
Then, diagonal of the square = 2r
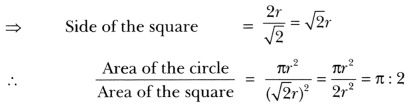
Short Answer :
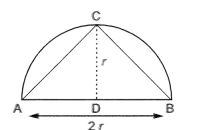
Area of largest ∆ABC = 12 × AB × CD
12 × 2r × r = r2 sq. units

rectangle = b cm
∴ Radius = b2 cm
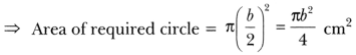
or r (2π – 1) = 37
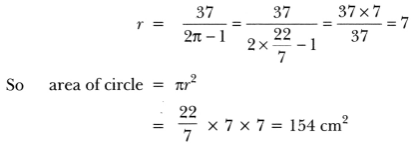
πr2 = p(8)2 + p(6)2
⇒ πr2 = 64p + 36p
⇒ pr2 = 100p
∴ r2 = 100pp = 100
⇒ r = 10cm
Hence, radius of required circle is 10 cm.
Perimeter = 66 cm
= πr + 2r = 66 [∴ Perimeter of a semicircle = πr + 2r]

Diameter = 2r cm and Circumference = 2πr cm
According to question,
Circumference = Diameter + 16.8
⇒ 2πr = 2r + 16.8
⇒ 2 × 227 × r = 2r + 16.8
⇒ 44r = 14r + 16.8 × 7
⇒ 44r – 14r = 117.6 or 30r = 117.6
⇒ r = 117.630 = 3.92
Hence, radius = 3.92 cm.
2πR = 396 and 2πr = 352
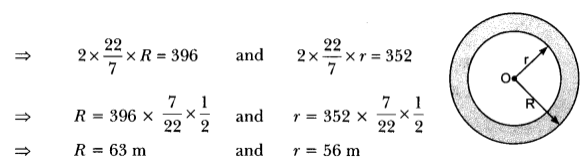
Hence, width of the track = (R – r) m = (63 – 56) m = 7 m
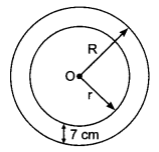
Let the inner and outer radii of the circular track berm and R m respectively. Then,
Inner circumference = 2πr = 220 m
![]()
Since the track is 7 m wide everywhere. Therefore,
R = Outer radius = r + 7 = (35 + 7)m = 42 m
∴ Outer circumference = 2πR = 2 × 227 × 42m = 264m
Rate of fencing = ₹ 2 per metre
∴ Total cost of fencing = (Circumference × Rate) = ₹(264 × 2) = ₹ 528
radius of the wheel = 40 cm.
Now, distance travelled in one complete revolution of wheel = 2π × 40 = 80π
Since, speed of the car is 66 km/h
So, distance travelled in 10 minutes = 66×100000×1060
= 11 × 100000 cm = 1100000 cm.
So, Number of complete revolutions in 10 minutes
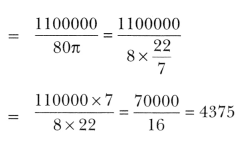
Long Answer :

Area of the shaded region
= ar (square) – 4 (ar of quadrant)
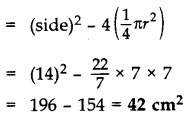
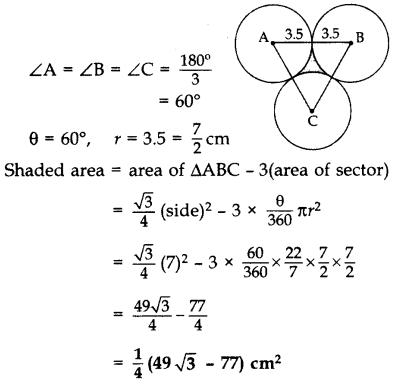
= 2(3.5) = 7 cm
∴ ∆ABC is an equilateral ∆
Area of the shaded region
= ar(square) – 4(circle)
= (side)2 – 4 (πr2)
= (28)2 – 4 × 227 × 7 × 7 = 784 – 616 = 168 cm2
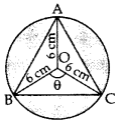
Area of shaded region
= 3(ar of minor segment) = 3[ar(minor sector) – ar(∆ABC)]
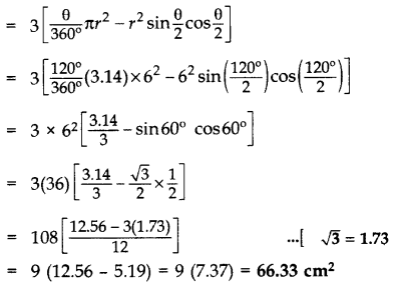
Case Study Answers:
Solution:
Radius of circle representing red region
![]()
Solution:
Area of red region πr2
![]()
Solution:
Radius of circle formed by combining red and silver region = Radius of red region + width of silver sign.
= (11+ 10.5)cm = 21.5cm
Solution:
Area of silver region = Area of combined region – Area of red region.
![]()
= 1452.78 – 380.28 = 1072.50cm2
Solution:
Area of circular path formed by two concentric circles ![]()
Let r and R be the radii of each smaller circle and larger circle, respectively.
We have, ![]()
![]()
Solution:
Area of smaller circle πr2
![]()
Solution:
Area of larger circle πR2
![]()
Solution:
Area of the black color region = Area of larger circle – Area of 4 smaller circles.
= 804.57 – 4 × 50.28 = 603.45cm2
Solution:
Area of quadrant of a smaller circle
![]()
Solution:
Area between two concentric circles
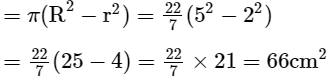
Assertion Reason Answer-






