
Areas Related to Circles
Areas Related to Circles
Number of revolutions in one minute =Distance moved in 1 minuteCircumference
Area enclosed by two concentric circles = πR2−πr2=π(R2−r2)=π(R+r)(R−r)
Where, R and r are radii of two concentric circles
 A diameter of circle divides a circle into two equal arcs, each known as a semi-circle.
A diameter of circle divides a circle into two equal arcs, each known as a semi-circle.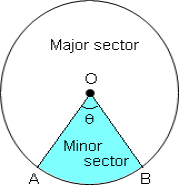 If the central angle of a sector is more than180°, then the sector is called a major sector and if the central angle is less than 180°, then the sector is called a minor sector.
If the central angle of a sector is more than180°, then the sector is called a major sector and if the central angle is less than 180°, then the sector is called a minor sector.
The segment which is smaller than the portion of semi-circle is called the minor segment and the segment which is larger than the portion of semi-circle is called the major segment. In the circle shown, the yellow portion is the minor segment while the non-shaded portion is the major segment.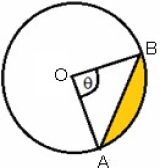
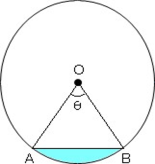
Area of the segment ACB = Area of sector OABC – Area of ∆ OAB
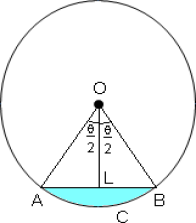 Area of segment ACB={Ѳ360°×πr2} –{sinѲ2+cosѲ2}
Area of segment ACB={Ѳ360°×πr2} –{sinѲ2+cosѲ2}
Area of a circle is πr2, where π=22/7 or ≈3.14 (can be used interchangeably for problem-solving purposes) and r is the radius of the circle.
π is the ratio of the circumference of a circle to its diameter.
Circumference of a Circle
The perimeter of a circle is the distance covered by going around its boundary once. The perimeter of a circle has a special name: Circumference, which is π times the diameter which is given by the formula 2πr
Segment of a Circle
A circular segment is a region of a circle that is “cut off” from the rest of the circle by a secant or a chord.
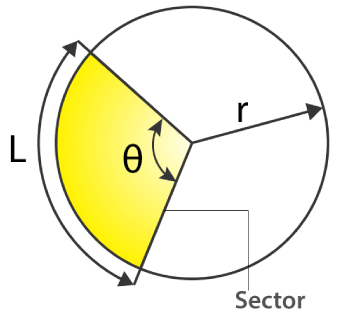
Sector of a Circle
A circle sector/ sector of a circle is defined as the region of a circle enclosed by an arc and two radii. The smaller area is called the minor sector and the larger area is called the major sector.
Angle of a Sector
The angle of a sector is the angle that is enclosed between the two radii of the sector.
Length of an arc of a sector
The length of the arc of a sector can be found by using the expression for the circumference of a circle and the angle of the sector, using the following formula:
L= (θ/360°)×2πr
Length of an arc of a sector
The length of the arc of a sector can be found by using the expression for the circumference of a circle and the angle of the sector, using the following formula:
L= (θ/360°)×2πr
where ∠θ is the angle of this sector (minor sector in the following case) and r is its radius
Area of a Triangle
The Area of a triangle is,
Area = (1/2) × base × height
If the triangle is an equilateral then
Area = (√3/4) × a2 where “a” is the side length of the triangle.
Area of a Segment of a Circle
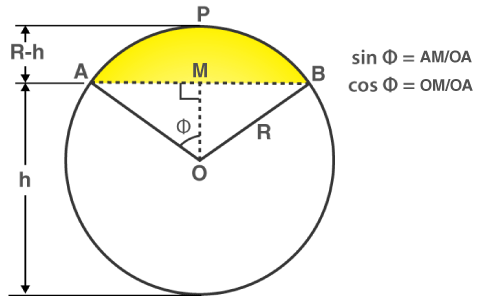
Area of segment APB (highlighted in yellow)
= (Area of sector OAPB) – (Area of triangle AOB)
= [(∅/360°) × πr2] – [(1/2) × AB × OM]
[To find the area of triangle AOB, use trigonometric ratios to find OM (height) and AB (base)]
Also, the Area of segment APB can be calculated directly if the angle of the sector is known using the following formula.
= [(θ/360°) × πr2] – [r2 × sin θ/2 × cosθ/2]
Where θ is the angle of the sector and r is the radius of the circle
All these formulas are tabulated as given below for quick revision.

Visualizations
Areas of different plane figures
Area of a square (side l) = l2
Area of a rectangle = l × b, where l and b are the length and breadth of the rectangle
Area of a parallelogram = b × h, where “b” is the base and “h” is the perpendicular height.
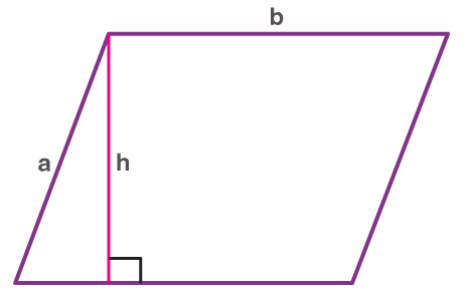
Parallelogram
Area of a trapezium = [(a + b) × h]/2,
where
a & b are the length of the parallel sides
h is the trapezium height
Area of a rhombus = pq/2, where p & q are the diagonals.
Area Of Shapes
In Geometry, a shape is defined as the figure closed by the boundary. The boundary is created by the combination of lines, points and curves. Basically, there are two different types of geometric shapes such as:
Two – Dimensional Shapes
Three – Dimensional Shapes
Each and every shape in the Geometry can be measured using different measures such as area, volume, surface area, perimeter and so on. In this article, let us discuss the area of shapes for 2D figures and 3D figures with formulas.
2D shapes
The two-dimensional shapes (2D shapes) are also known as flat shapes, are the shapes having two dimensions only. It has length and breadth. It does not have thickness. The two different measures used for measuring the flat shapes are area and the perimeter. Two-dimensional shapes are the shapes that can be drawn on the piece of paper. Some of the examples of 2D shapes are square, rectangle, circle, triangle and so on.
Area of 2D Shapes Formula
In general, the area of shapes can be defined as the amount of paint required to cover the surface with a single coat. Following are the ways to calculate area based on the number of sides that exist in the shape, as illustrated below in the fig.
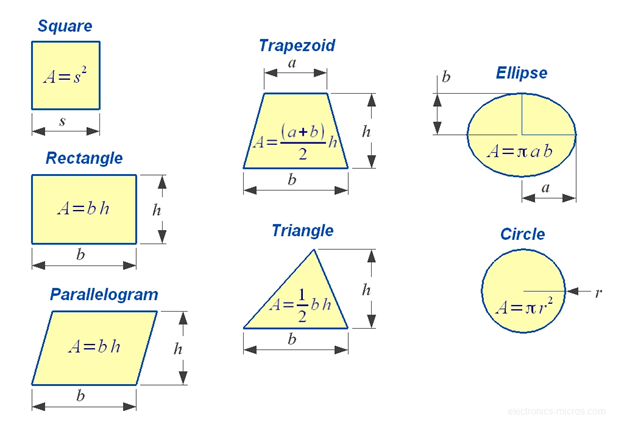
Let us write the formulas for all the different types of shapes in a tabular form.
|
Shape |
Area |
Terms |
|
Circle |
π × r2 |
r = radius of the circle |
|
Triangle |
½ × b × h |
b = base h = height |
|
Square |
a2 |
a = length of side |
|
Rectangle |
l × w |
l = length w = width |
|
Parallelogram |
b × h |
b=base h=vertical height |
|
Trapezium |
½(a+b) × h |
a and b are the length of parallel sides h = height |
|
Ellipse |
πab |
a = ½ minor axis b = ½ major axis |
Areas of Combination of Plane figures
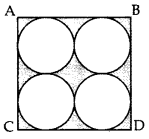
For example: Find the area of the shaded part in the following figure: Given the ABCD is a square of side 28 cm and has four equal circles enclosed within.
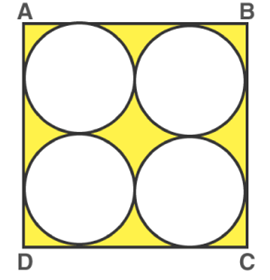
Area of the shaded region
Looking at the figure we can visualize that the required shaded area = A(square ABCD) − 4 × A(Circle).
Also, the diameter of each circle is 14 cm.
= (l2) −4 × (πr2)
= (282) − [4 × (π × 49)]
= 784 − [4 × 22/7 × 49]
= 784 − 616
= 168cm2
Important Questions
Multiple Choice questions-
1. Perimeter of a sector of a circle whose central angle is 90° and radius 7 cm is
(a) 35 cm
(b) 25 cm
(c) 77 cm
(d) 7 cm
2. The area of a circle that can be inscribed in a square of side 10 cm is
(a) 40π cm²
(b) 30π cm²
(c) 100π cm²
(d) 25π cm²
3.The perimeter of a square circumscribing a circle of radius a units is
(a) 2 units
(b) 4α units
(c) 8α units
(d) 16α units
4. The perimeter of the sector with radius 10.5 cm and sector angle 60° is
(a) 32 cm
(b) 23 cm
(c) 41 cm
(d) 11 cm
5. In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre, where π = 227 then length of arc is:
(a) 11 cm
(b) 227 cm
(c) 22 cm
(d) 44 cm
6. The perimeter of a sector of radius 5.2 cm is 16.4 cm, the area of the sector is
(a) 31.2 cm²
(b) 15 cm²
(c) 15.6 cm²
(d) 16.6 cm²
7. If the perimeter of a semicircular protractor is 72 cm where π = 227, then the diameter of protractor is:
(a) 14 cm
(b) 33 cm
(c) 28 cm
(d) 42 cm
8. If the radius of a circle is doubled, its area becomes
(a) 2 times
(b) 4 times
(c) 8 times
(d) 16 times
9. If the sum of the circumferences of two circles with radii R1 and R2 is equal to circumference of a circle of radius R, then
(a) R1 + R2 = R
(b) R1 + R2 > R
(c) R1 + R2 < R
(d) Can’t say.
10. The perimeter of a circular and square fields are equal. If the area of the square field is 484 m² then the diameter of the circular field is
(a) 14 m
(b) 21 m
(c) 28 m
(d) 7 m
Very Short Questions:
Short Questions :
Long Questions :
Assertion Reason Questions-
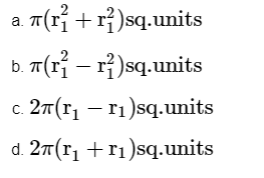

Case Study Answers:
Assertion: If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason: Circumference = 2π × radius
Assertion: If a wire of length 22 cm is bent is the shape of a circle, then area of the circle so formed is 40 cm.
Reason: Circumference of the circle = length of the wire.






