
Applications-of-Derivatives
Important Questions
Multiple Choice questions-
1. The rate of change of the area of a circle with respect to its radius r at r = 6 cm is:
(a) 10π
(b) 12π
(c) 8π
(d) 11π
2. The total revenue received from the sale of x units of a product is given by R(x)=3x²+36x+5. The marginal revenue, when x = 15 is:
(a) 116
(b) 96
(c) 90
(d) 126.
3. The interval in which y = x² e-x is increasing with respect to x is:
(a) (-∞, ∞)
(b) (-2,0)
(c) (2, ∞)
(d) (0, 2).
4. The slope of the normal to the curve y = 2x² + 3 sin x at x = 0 is
(a) 3
(b) 13
(c) -3
(d) –13
5. The line y = x + 1 is a tangent to the curve y² = 4x at the point:
(a) (1, 2)
(b) (2, 1)
(c) (1, -2)
(d) (-1, 2).
6. If f(x) = 3x² + 15x + 5, then the approximate value of f(3.02) is:
(a) 47.66
(b) 57.66
(c) 67.66
(d) 77.66.
7. The approximate change in the volume of a cube of side x meters caused by increasing the side by 3% is:
(a) 0.06 x³ m³
(b) 0.6 x³ m³
(c) 0.09 x³m³
(d) 0.9 x³ m³
8. The point on the curve x² = 2y, which is nearest to the point (0, 5), is:
(a) (2 √2, 4)
(b) (2 √2, 0)
(c) (0, 0)
(d) (2, 2).
9. For all real values of x, the minimum value of 1−x+x21+x+x2 is
(a) 0
(b) 1
(c) 3
(d) 13
10. The maximum value of [x (x – 1) + 1]1/3, 0 ≤ x ≤ 1 is
(a) (13)1/3
(b) 12
(c) 1
(d) 0
Very Short Questions:
f(x) = 4x3 – 18×2 – 27x – 7 is always increasing in R. (C.B.S.E. 2017)
x = at2, y = 2at t = 2.
(i) f(x) = (2x-1)2 + 3
(ii) f(x)= 16x2 – 16x + 28
(iii) f(x) = -|x+ 1| + 3
(iv) f(x) = sin 2x + 5
(v) f(x) = sin (sin x).
Long Questions:
Assertion and Reason Questions:
1. Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
Assertion(A):For each real ‘t’, then exist a point C in [t,t+π]
such that f′(C) = 0
Reason (R):f(t)=f(t+2π) for each real t
2. Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes(a), (b), (c) and (d) as given below.
Assertion (A):One root of x3−2x2−1= 0 and lies between 2 and 3.
Reason(R):If f(x) is continuous function and f [a], f[b] have opposite signs then at least one or odd number of roots of f(x)=0 lies between a and b.
Case Study Questions:
1. An architecture design a auditorium for a school for its cultural activities. The floor of the auditorium is rectangular in shape and has a fixed perimeter P.

Based on the above information, answer the following questions.


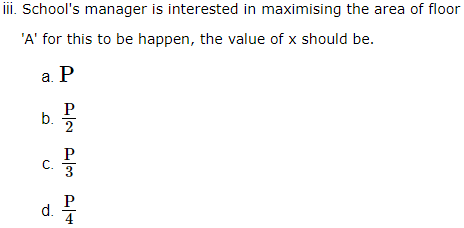

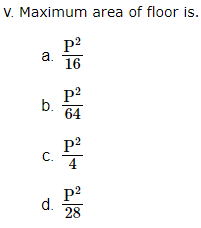
2. Rohan, a student of class XII, visited his uncle’s flat with his father. He observe that the window of the house is in the form of a rectangle surmounted by a semicircular opening having perimeter 10m as shown in the figure.
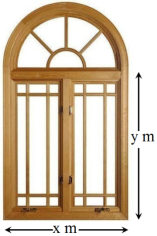
Based on the above information, answer the following questions.
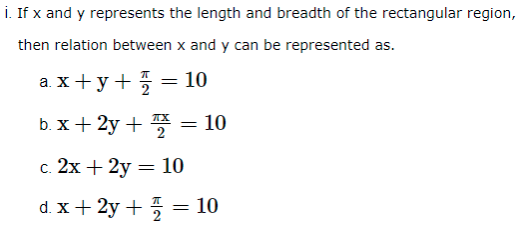
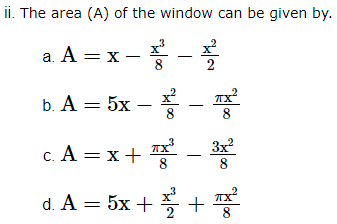



Answer Key-
Multiple Choice questions-
Very Short Answer:
The given curve is y = 5x – 2x3
∴dydx = 5 – 6x2
i.e., m = 5 – 6x2,
where ‘m’ is the slope.
∴dmdt = –12x dxdt = -12x (2) = -24x
∴dmdt]x=3 = -24(3) = -72.
Hence, the rate of the change of the slope = -72.
Let x1 and x2∈ R.
Now x1> x2
⇒ 7x1> 7x2
⇒ 7x1– 3 > 7x2– 3
⇒ f(x1) > f(x2).
Hence, ‘f’ is strictly increasing function in R.
We have: f(x) = 4x3 – 18 × 2 – 27x – 7
∴ f(x) = 12x2– 36x + 27 = 12(x2– 3x) + 27
= 12(x2 – 3x + 9/4) + 27 – 27
= 12(x – 3/2)2∀ x∈ R.
Hence, f(x) is always increasing in R.
The given curve is x – at2, y = 2at.
∴dxdt = 2at
dxdt = 2a
∴dydx = dy/dtdx/dt = 2a2at =
Hence, slope of the tangent at t = 2 is: dydx]t=2 = 12
(i) We have:
f(x) = (2x – 1)2 + 3.
Here Df = R.
Now f(x) ≥ 3.
[∵ (2x – 1)2≥ 0 for all x ∈ R]
However, maximum value does not exist.
[∵ f(x) can be made as large as we please]
(ii) We have:
f(x) = 16x2 – 16x + 28.
Here Df = R.
Now f(x) = 16 (x2 – x + 14 + 24
= (16(x – 12 )2 + 24
⇒ f(x) ≥ 24.
[∵ 16(x – 12)2 ≥ 0 for all x ∈ R
Hence, the minimum value is 24.
However, maximum value does not exist.
[ ∵ f(x) can be made as large as we please]
(iii) We have :
f(x) = – 1x + 11 + 3
⇒ f(x) ≤ 3.
[ ∵ -|x + 1| ≤ 0]
Hence, the maximum value = 3.
However, the minimum value does not exist.
[∵ f(x) can be made as small as we please]
(iv) We have :
f(x) = sin2x + 5.
Since – 1 ≤ sin 2x ≤ 1 for all x ∈ R,
– 1+5 ≤ sin2x + 5 ≤ 1+5 for all x∈ R
⇒ 4 ≤ sin2x + 5 ≤ 6 for all x ∈ R
⇒ 4 ≤ f(x) ≤ 6 for all x ∈ R.
Hence, the maximum value = 6 and minimum value = 4.
(v) We have :
f(x) = sin (sin x).
We know that – 1 ≤ sin x ≤ 1 for all x ∈ R
⇒sin(-1) ≤ sin(sinx) ≤ sin 1 for all x ∈ R
⇒– sin 1 ≤ f(x) ≤ sin 1.
Hence, maximum value = sin 1 and minimum value = -sin 1.
The given curve is x2 = 2y …(1)
Diff.w.r.t.t, 2x dxdt = 2 dydt
⇒ 2x dxdt = 2 dxdt
∵dydt = dxdt given
From (1), 1 = 2y ⇒ y = 12
Hence, the reqd. point is (1, 12)
Long Answer:
![]()
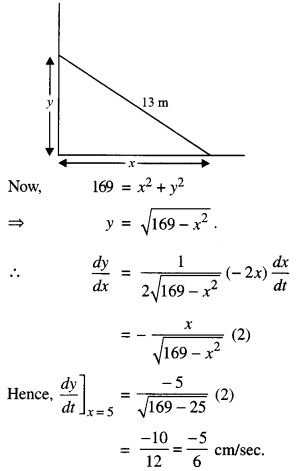
Hence, the height is decreasing at the rate of 5/6 cm/sec.
The given curves are:
x2 + y2 = 4 ………….(1)
(x – 2)2 + y2 = 4 ………….. (2)
From (2),
y = 4 – (x – 2)2
Putting in (1),
x2 + 4 – (x – 2)2 = 4
⇒ x2– (x – 2)2 = 0
⇒ (x + (x – 2)(x – x) + 2) = 0
⇒ (2x –2)(2) = 0
⇒ x = 1.
Putting in (1),
1 + y2 = 4
⇒ y = √3
∴ Point of intersection = (1, √3 )
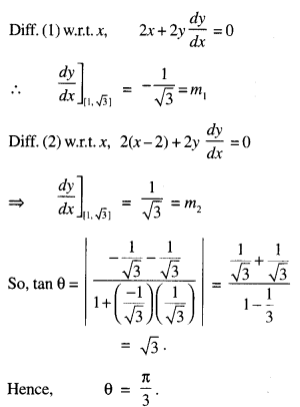
Given function is:
f(x) = – 2x3 – 9x2 – 12x + 1.
Diff. w.r.t. x,
f'(x) = -6x2 – 18x – 12
= -6(x + 1) (x + 2).
Now, f'(x) – 0
⇒ x = -2, x = -1
⇒ Intervals are (-∞– 2), (-2, -1) and (-1, ∞).
Getting f’ (x) > 0 in (-2, -1)
and f'(x) < 0 in (-∞, -2) u (-1, ∞)
⇒ f(x) is strictly increasing in (-2, -1) and strictly decreasing in (-∞, 2) u (-1, ∞).
Let ‘x’ and ‘y’ be the length and breadth of the rectangle ABCD.
Radius of the semi-circle = x2.
Circumference of the semi-circle = πx2

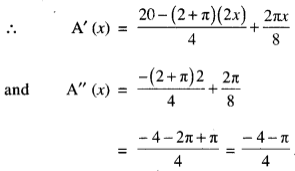
or Max ./Min. of A (x), A’ (x) = 0
![]()
20 – (2 + π)(2x) + πx = 0
20 + x(π – 4 – 2π) = 0
20 – x(4 + π) = 0
![]()
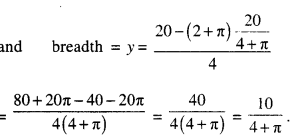
![]()
Case Study Answers:
1. Answer :
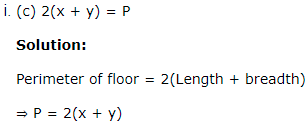
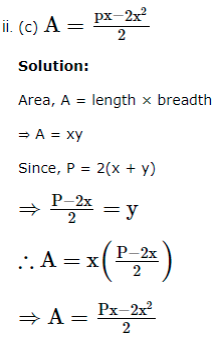
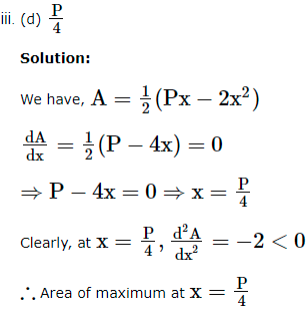
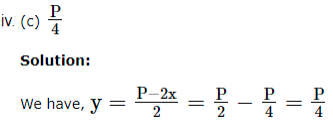
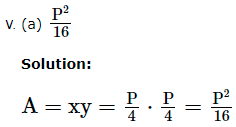
2. Answer :

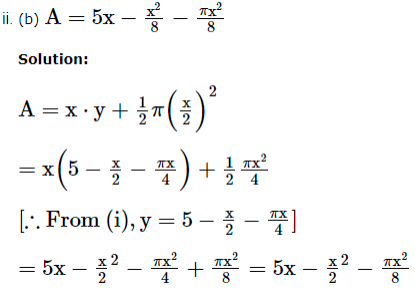
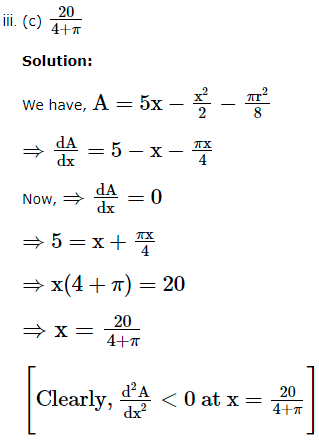

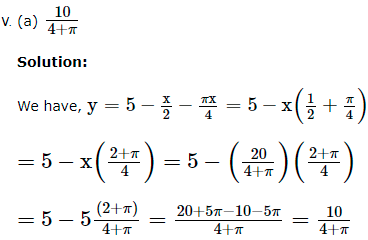
Assertion and Reason Answers:
1. a) Both A and R are true and R is the correct explanation of A.
Solution:
Given that f(x)=2+cosx
Clearly f(x) is continuous and differentiable everywhere Also f′(x) = −sinx⇒ f′(x=0)
⇒ −sinx = 0 ⇒ x = nπ
∴ These exists C ∈ [t, t+π] for t ∈ R
such that f′ (C) = 0
∴ Statement-1 is true Also
f(x) being periodic function of period 2π
∴ Statement-2 is true, but Statement-2 is not a correct explanation of Statement -1.
2. (a) Both A and R are true and R is the correct explanation of A.
Solution:
Given f(x)=x3−2x2−1=0
Here, f(2)=(2)3−2(2)2−1=8−8−1=−1
and f(3)=(3)3−2(3)2−1=27−18−1=8
∴f(2)f(3)=(−1)8=−8<0
⇒ One root of f(x) lies between 2 and 3
∴ Given Assertion is true Also Reason R is true and valid reason
∴ Both A and R are correct and R is correct explanation of A.






