Brain teasers in Bengali | Buddhir Bangla dhadha |Bengali Riddles

The Power of Daily Bengali Riddle-Solving

প্রতিদিন ধাঁধা (Bengali Riddles) সমাধান করা আপনার মস্তিষ্ককে একটি দৈনিক ওয়ার্কআউটের মতো শাণিত করে। এই ধাঁধাগুলো (Brain teasers in Bengali | Buddhir Bangla dhadha |Bengali Riddles) আপনাকে বিভিন্ন প্যাটার্ন বা ধরন শনাক্ত করতে, ভিন্নভাবে চিন্তা করতে এবং অসংলগ্ন ধারণাগুলোর মধ্যে সংযোগ স্থাপন করতে বাধ্য করে আপনার চিন্তাশক্তিকে বৃদ্ধি করে—যা জ্যামিতিক সমস্যা সমাধান, আইনি খসড়া তৈরি বা আর্থিক বিশ্লেষণের মতো দক্ষতার জন্য অত্যন্ত গুরুত্বপূর্ণ।

সৃজনশীলতা জাগিয়ে তুলতে, মনোযোগ বাড়াতে এবং শেখার বিষয়টিকে আনন্দদায়ক করতে দিনে একটি করে ধাঁধা দিয়ে শুরু করুন। সময়ের সাথে সাথে আপনি নিজের তীক্ষ্ণ বুদ্ধি এবং দ্রুত অন্তর্দৃষ্টি লক্ষ্য করবেন।

সূচীপত্র

বুদ্ধির ধাঁধা

 

1. নিম-এর খেলা

2. ঘোড়ার সঙ্গে ঘোরাঘুরি

3. জালিয়াতির জ্বালা

4. বইএর পোকা

5. নামাবলি

6. ছেলের হাতের মোয়া

7. কয়েদীর কেরামতি

8. সত্যাসত্য

9. শহীদ মক্ষিকা

10. ছোট্টো কিন্তু বড়ো সমস্যা

11. তুরুপের রং

12. গয়লার কেরামতি

13. ভাই-ভাই

14. ঝিঝিপোকার কান্না

15. বাঘা দাবাড়ের কাও

16. দুধে-জলে

17. প্রচ্ছন্ন পাটীগণিত

18. বন্দী পতঙ্গ

19. খনরাম দাসের দিনপঞ্জি থেকে

20. আপত্তিকর চিঠিচাপাটি

21. বাটপাড়িয়া হত্যারহস্য

22. যাদুবর্গ ও কিয়াহুব

23. পায়ে ধরে সাধা

24. দস্তুরমতো দরদস্তুর

25. খপ্পট অ্যাভিনিউ-এর ডাকপিয়ন

26. দুঃসাহসিক ভ্রমণকাহিনী

27. জন্মদিনের কেক

28. হবুচন্দ্র রাজার গোলটেবিল

29. বিভাজ্যতা

30. উড়নচণ্ডীতলা হাউসিং এস্টেট

31. বাজাব করার হাজার ঠ্যালা

32. টোপোলজি

33. পৃথিবীৰ সূত্ৰবল য

34. নোন্তার বুদ্ধি

35. হ য ব ব ন্স-র বিচার সভা

36. স্বল্পতম দূরত্ব

37. পাঁচে বহুতল ছয়ে গ্রহ

38 কাটাকুটি খেলা

39. বাসা বদল

40. একটি খুচরো সমস্যা

41. ঘড়ি ভাগ

42. দ্যাখার ভুল

43 রাজাব খেলা দাবা টোপোলজির খেলা

44. টোপোলজির খেলা

45. তাসের দেশ

46. ব্রহ্মগুপ্তের সমস্যা

47. ঘরে-বাইরে

48. হাতি-গলা ফাঁক

49. লীলাময়বাবুর লীলাখেলা

50. ভূতুড়ে গেট

51. সাংখ্যদর্শন

52. ধাঁধালি

.

.

1. নিম-এর খেলা

দুজনে মিলে ঘরে বসে যত রকম খেলা খেলা যায়, তার মধ্যে সবচেয়ে চালু হলো কাটাকুটি। কিন্তু একটু বড়ো হলেই খেলাটার মজা চলে যায়। একেবারে অন্যমনস্ক না হলে প্রত্যেকবারই ড্র হবে। কিন্তু নিম-এর খেলার ( NIM GAME) ব্যাপারই আলাদা । অনেকে বুড়ো বয়েস পর্যন্ত হেরেই চলেন, কী করে জেতে কিছুতেই বুঝে উঠতে পারেন না। আর কিছু ছেলে খেলাটা শেখার পরেই একটু মাথা খাটিয়ে ব্যাপারটা বুঝে নেয়, ফলে শুধুই জিতে চলে।

নিম-এর খেলা বোধহয় প্রথম চালু হয়েছিল চীনে। খেলাটার নাম ‘নিম‘ দিয়েছিলেন হার্ভার্ড বিশ্ববিদ্যালয়ের অংক-র অধ্যাপক চার্লস লিওনার্ড বুটন । 1901 সালে তিনিই খেলাটা বিশ্লেষণ করেন। পুরনো ইংরেজিতে ‘নিম‘ মানে সরিয়ে নেয়া বা হাত সাফাই

করা। উইলিয়াম শেকসপিয়রের ‘দা মেরি ওআইভস্ অব উইনসর‘ নাটকে

.

.

নিম বলে একটি চরিত্র আছে। ভদ্রলোকের আবার একটু হাতটান ছিল। জর্মন ভাষায় nehmeeins, মানে একটা নাও। আর কাগজটা ঘুরিয়ে পড়লে NIM শব্দটা দেখাবে WIN, কারণ M- কে 180° ঘোরালে W হয়ে যায়, I আর N-এর চেহারা একটুও পালটায় না।

অনেক গৌরচন্দ্রিকা হলো । এবার খেলাটায় আসা যাক। ধরা যাক দুর্যোধন আর যুধিষ্ঠির নিম খেলতে বসেছেন। তিন সারি দেশলাই কাঠি সাজিয়ে রাখা আছে। প্রথমটায় তিনটে, দ্বিতীয়টায় 5টা, তৃতীয়টায় 7টা। একবার যুধিষ্ঠির একবার দুর্যোধন এক একটি সারি থেকে যে-ক-টা ইচ্ছে কাঠি টানবেন, এমনকি পুরো একটা সারিও টানতে পারেন । তবে একই সঙ্গে দুটো সারি থেকে কাঠি টানা চলবে না। দুজনের টানাটানিতে শেষ অবধি যে-কোনো সারির একটা মাত্র কাঠি পড়ে থাকবে। যিনি শেষ কাঠিটি টানতে বাধ্য হবেন, তাঁর হার ।

যুধিষ্ঠিরই প্রথম টানবেন। তিনি প্রথম সারির একটা কাঠি নিলেন। দুর্যোধন হেসে ঐ সারিরই বাকি দুটো কাঠি টেনে নিলেন । যুধিষ্ঠির ভুরু কুঁচকে তৃতীয় সারির তিনটে কাঠি নিলেন। দুর্যোধন ঐ সারিরই একটা কাঠি টানলেন । যুধিষ্ঠির দ্বিতীয় সারির পাঁচটা কাঠিই তুলে নিলেন। দুর্যোধন এক গাল হেসে বললেন, সত্যি দাদা, তোমার মতো লোক হয় না। বলে তিনটে কাঠির দুটো তুলে নিলেন। একটা পড়ে রইল যুধিষ্ঠিরের জন্যে। অতএব তাঁর হার ।

বলে রাখা ভালো, দুজনেই পুরো আন্দাজে খেলেছেন। কারুরই কোনো ‘প্লান’ ছিল না । কিন্তু, বুদ্ধিমান পাঠক ভেবে-চিন্তে দ্যাখো তো, কার জেতার সম্ভাবনা বেশি: যে প্রথমে টানবে, না যে তার পরে টানবে। দ্বিতীয় কথা, প্রথমবার কোন্ সারি থেকে ক-টা কাঠি টানলে প্রথম খেলোয়াড় জিতবেই?

.

.

2. ঘোড়ার সঙ্গে ঘোরাঘুরি

॥ ক ॥

পক্ষীরাজটার ক-দিন হলো পেটব্যথা। রাজপুত্র বাধ্য হয়েই এমনি ঘোড়ায় চড়লেন । অনেক দূর যেতে হবে—তেপান্তরের মাঠ পেরিয়ে আরো অনেকটা ।

রাজপুত্র চলেছেন, চলেছেন, চলেছেন। হঠাৎ পেছন থেকে এক ঝলক গরম হাওয়া ঘাড়ে লাগলো। পেছনে তাকিয়ে দ্যাখেন– সর্বনাশ ! ঝাঁ ঝাঁ রোদ্দুরে এমনেই মাথা গরম হয়ে গেলো, এখন চোখদুটো সকেট থেকে বেরিয়ে আসার জোগাড়। পেছনের সমস্ত ঘাসে আগুন ধরে গেছে, প্রায় বেড়াজাল দিয়ে রাজপুত্রকে গ্রাস করতে আসচে। ঘোড়া যদি ঘণ্টায় ষাট মাইল জোরে যায়, হাওয়া বইছে সত্তর মাইল বেগে । যত জোরেই ঘোড়া ছোটাও, নিস্তার নেই । এতো আর পক্ষীরাজ নয় যে উড়ে যাবে। রাজপুত্র এধার-ওধার দেখে ঘোড়াটাকে দাঁড় করালেন–

শেষ পর্যন্ত রাজপুত্র দিব্যি তেপান্তর পেরোলেন । কী করে?

.

॥ খ ॥

রাজা কৃষ্ণচন্দ্র মরার সময় মন্ত্রীকে বলে গেলেন, আমি মরলে বড়ো ছেলেই রাজা হবে । তবে আমার সমস্ত সম্পত্তি ভাগ হবে এই ভাবেঃ বড়ো রাজপুত্র পাবে $\frac{1}{2}$, মেজো পাবে $\frac{1}{3}$ আর ছোটো $\frac{1}{9}$ ।

আর সব ঠিকঠাক হলো, শুধু সমস্যা হলো আস্তাবল নিয়ে। সতেরোটা ঘোড়া, তার $\frac{1}{2},\frac{1}{3},\frac{1}{9}$ হবে কী করে ? মহা মুশকিল । মন্ত্রী তো মাথা চুলকে অস্থির, তিন রাজপুত্রেরও তথৈবচ। ডাকো গোপাল ভাঁড়কে, যদি একটা মুশকিল আসান করতে পারে ।

গোপাল ভাঁড় এক টাট্টু, ঘোড়ায় চড়ে হাজির। সবাই বলে,কি হে গোপাল, তোমার আবার ঘোড়া কেন ? কান এঁটো করে হেসে গোপাল বললো, ঘোড়া ভাগাভাগির ব্যাপার, ঘোড়ায় না চড়লে চলে?

দিব্যি ভাগাভাগি হলো। সবাই খুশি। কী করে?

.

॥ গ ॥

এ এক অদ্ভুত স্বয়ম্বরা । রাজকন্যা কি পণ করেছেন সবচেয়ে আনাড়ি লোককে মালা দেবেন! হুলুস্থুলু কাণ্ড ।

রাজকন্যার দুটি ঘোড়া আছে। একটা কপ্পুরের মতো সাদা, অন্যটা শ্রাবণের মেঘের মতো কালো। যাঁরা স্বয়ম্বরায় আসবেন, তাঁদের মধ্যে থেকে দুজনকে বেছে নেয়া হবে । তার পরেই আসল পরীক্ষা। দুজনকে দুটি ঘোড়ায় উঠে ঐ দূরের নর্মদা নদীর জল আনতে হবে। যে-ঘোড়া শেষে পৌঁছবে তার জিৎ!

অঙ্গ আর কলিঙ্গের দুই রাজপুত্রই দ্যাখা গেলে। ভাগ্যবান্ । রাজকন্যা তাদেরই বেছে নিলেন। দুই রাজপুত্র ছুটলো ঘোড়ায় চড়ে। অঙ্গ সাদায়, কলিঙ্গ কালোয়। নর্মদার জল নিয়ে দুজনেই দাড়িয়ে পড়লো। অঙ্গ দাঁত খিঁচিয়ে বললো, যা-না, দাঁড়িয়ে আছিস্ কেন? কলিঙ্গ বললো, আহা, তুই আগে যা ।

এক সন্ন্যাসী দূরে বসে সমস্ত ঘটনাটা দেখছিলেন। এবার কাছে গিয়ে জিগেস করলেন ব্যাপারটা কী। ঘোঁৎঘোৎ করে দুজনেই বললো। সন্ন্যাসী দুজনেরই কানে কানে কী যেন বললেন। ব্যস, ছুট ছুট। দুজনেই প্রাণপণে ঘোড়া ছোটালো ।

অঙ্গই জিতলো। কী করে?

.

3. জালিয়াতির জ্বালা

কোট-প্যান্ট পরা এক ভদ্দরলোক এলেন সাবিত্রী বস্ত্রালয়ে। চল্লিশ বাণ্ডিল কাপড় দেখে একটা শাড়ি পছন্দ হলো। তারপর শুরু হলো দর কষাকষি। শেষ অবধি তিরিশ টাকায় রফা হলো । অত কমে রফা করতে দোকানীর ইচ্ছে ছিল না। কিন্তু বউনি বলে কথা ।

ভদ্দরলোক একটা একশ টাকার নোট দিলেন। সাবিত্রী বস্ত্রালয়ে অত টাকার ভাঙানি ছিল না। দোকানী পাশের এক দোকান থেকে দশটাকার নোট এনে সত্তর টাকা ফেরৎ দিলেন। ভদ্দরলোকও টাকাটা যত্ন করে কোটের ভেতরের পকেটে পুরে, শাড়িটি নিয়ে চলে গেলেন।

ঘণ্টাখানেক বাদে পাশের দোকানী এসে বলেন কিনা ঐ একশ টাকার নোটটা জাল ! সাবিত্রী বস্ত্রালয়ের তো মাথায় হাত। কী আর করবেন, নোটটা উলটেপালটে দেখে একশ টাকা ফেরৎ দিতে হলো।

সাবিত্রী বস্ত্রালয়ের তাহলে কত টাকা ক্ষতি হলো?

.

4. বইএর পোকা

সব জায়গায় যা হয়, মরণচাঁদ স্মৃতি পাঠাগারেও তাই হয়েছে। ভালো লেখকের ভারি বই বাজারে কাটে না, পোকায় কাটে। শ্রীশ্রীশচন্দ্র তর্কচঞ্চুর দশ খণ্ডের বই ‘মানবাত্মা ও জীবদেহের অন্যোন্য সম্পর্ক বিষয়ে গোস্বামীর সহিত বিচার, প্রতি খণ্ডে পাঁচশ করে পাতা। দশটা খণ্ডই পরপর সাজানো পড়ে ছিল, কেউ কখনো পড়ে নি। হঠাৎ কোন গবেষকের দরকার পড়েছে। তাক থেকে সেগুলো নাবিয়ে দ্যাখে— সর্বনাশ ! লেপিস্‌মা বলে সেই খানদানি পোকা প্রথম খণ্ডের প্রথম পাতা থেকে শেষ খণ্ডের শেষ পাতা পর্যন্ত সোজা কেটে চলে গেছে।

কথা হলো, ঐ দশ খণ্ডের মোট কত পাতা পোকার খোরাক হয়েছে?( মলাট বা মলাট খুললেই যে পুস্তনির সাদা পাতা থাকে, সে-সব হিসেব থেকে বাদ)

.

5. নামাবলি

ধাঁধা ব্যাপারটা বোধহয় সংক্রামক। না হলে আমাদের পাড়ার জাঁদরেল হেডমিস্ট্রেস, যাঁর গলা শুনলে মুলতানি গরু দুধের বদলে দই দেয়, তিনিও কিনা আমাদের সঙ্গে ধাঁধা করতে শুরু করেন ! সেদিন আমাদের দপ্তরে বসে বললেন : জানোই তো, ইস্কুল-কলেজের বন্ধুদের সঙ্গে এখন আর বড়ো একটা দ্যাখা-ট্যাখা হয় না । কুম্ভ কোণমের রাস্তায় হঠাৎ একজনকে দেখতে পেলুম, স্কটিশে আমার সঙ্গে পড়তো। সঙ্গে দেখি একটি বাচ্চা ছেলে। প্রায় এক যুগ বাদে দ্যাখা। অ্যাদ্দিন বেঁচে ছিল তাই জানতুম না । তা জিগেস করলুম, ছেলেটি কার। বললো, ওরই ছেলে, এবার নাকি ইস্কুলে ভর্তি হবে। ছেলেটিকে জিগেস করলুম, এই, তোর নাম কী রে? তো লাজুক গলায় বললো, বিত্তচঞ্চল রায়। আমি বললুম, বাঃ, বেশ বাবার নামের সঙ্গে মিলিয়ে নাম হয়েছে তো।এই অবধি বলে, রক্ত-জল-করা গলায় হেডমিস্ট্রেস বললেন, বলো দিকি, কী করে নামের মিল ধরলুম ।

.

6. ছেলের হাতের মোয়া

হাটে পাঠানোর আগে মা পইপই করে বলে দিলেন, এই দু হাঁড়ি মোয়া দিলুম, একটা মোয়া দশ পয়সা, জোড়া বিশ পয়সা, পয়সা হাতে পেলে তবে মোয়া দিবি । কানাই বলাই দুই ভাই, কাঁধে দু হাঁড়ি মোয়া নিয়ে বেরোলো। খানিক দূর যেতেই কানাই বললো, এই বলা, তোর হাঁড়ি থেকে একটা মোয়া দে-না। বলাই সাবধানী ছেলে । ঘাড় নেড়ে বললো, ওসব হবে না । ফ্যালো কড়ি মাখো তেল ।

হাটের পথে গাজনকাকুর সঙ্গে দ্যাখা। তিনি মোয়া-রসিক, নগদা পয়সা দিয়ে একটি মোয়া খেতে খেতে চলে গেলেন। হাটে পৌঁছতে না পৌঁছতে ন্যায্য দামে সব মোয়া বিক্রি হয়ে গেলো। দিনের শেষে শূন্য হাঁড়ি নিয়ে দু ভাই বাড়ি ফিরলো ।

মা খুশি হয়ে বললেন, লক্ষ্মী ছেলে, সব মোয়া বিক্রি হয়ে গেছে? এবার হাত মুখ ধুয়ে দুটো মোয়া খা, তোদের জন্যেই তুলে রেখেচি। তারপর পয়সাকড়ি দে ।

কানাই ট্যাক থেকে দশটি পয়সা বার করে দিলো। ব্যস, আর পয়সা ঠেকানোর নাম নেই। মা তো অবাক। কিন্তু দুই ভাইই জোর করে বললো, তোমার কথার একটুও নড়চড় করিনি। বিনি পয়সায় একটা মোয়াও বেচি নি।

কী ভাবে এটা হলো?

.

7. কয়েদীর ক্রোমতি

গোপাল ভাঁড়ের সঙ্গে থেকে থেকে রাজা কৃষ্ণচন্দ্রের মাথায় কিছু পোকা ঢুকেছিল। তিনজন দাগী আসামী –ডাকাতি, রাহাজানি আর খুনের দায়ে ধরা পড়েছে, ফাঁসি হবেই হবে। রাজা বললেন, তোমাদের বুদ্ধির পরীক্ষা হবে। যদি পাশ করো তো সব খুন মাফ ৷

তিন জনকেই চোখ বেঁধে দাঁড় করানো হলো । পাচটা টুপি আনা হয়েছে—তিনটে লাল রঙের, দুটো কালো। পাঁচটার মধ্যে থেকে যে-কোনো তিনটে টুপি তাদের মাথায় পরিয়ে দেয়া হলো । বাকি দুটো পড়ে রইলো। তারপর তিনজনকে এর–পেছনে-ও-এর– পেছনে-সে করে দাঁড় করিয়ে চোখের বাঁধন খুলে দেয়া হলো। প্রথম কয়েদী তাহলে সামনের দুজনকে দেখতে পাচ্ছে, দ্বিতীয় কয়েদী দেখছে একজনকে, তৃতীয় কয়েদী কাউকেই দেখতে পাচ্চে না। রাজা বললেন, বলো, তুমি কোন্ রঙের টুপি পরে আছ।

প্রথম কয়েদী কাতরভাবে বললো, জানি না মহারাজ, তবে আমার সামনে রাজা বললেন, চোপ!

দ্বিতীয় কয়েদী কাঁদো কাঁদো গলায় বললো, পারলুম না মহারাজ, তবে—রাজা বললেন, চোপরাও !

তৃতীয় কয়েদী ঝপ, করে বললো, আমি বলবো মহারাজ? বলে ঠিক উত্তরটাই দিলো ।

লোকটা কী উত্তর দিয়েছিল? কী করেই বা বললো?

8 সত্যাসত্য

শিশিরদের মেস থেকে রেগেমেগে বেরিয়ে ঘনাদা কোথায় যান? এটা কোনো ধাঁধা নয়! সাধারণত মাছ বা হাঁস বা জানলা বা ফুটো নিয়ে ঝামেলা হয় । আর ঘনাদাও ঐ অছিলায় বেরিয়ে পড়ে আমাদের আড্ডায় পায়ের ধুলো দিয়ে যান।

সেদিন গম্ভীর মুখ করে এসে ঘনাদা তো বসলেন । তখন তুমুল তর্ক চলচে। বেচারা ভুলান বাগবাজারের কাঁটাপুকুর লেনে এক মাস্টারের সঙ্গে দ্যাখা করতে গেলো। ঠিকানা জানতো না, তাই ও-পাড়ার রকে-বসা ছেলেদের জিগেস করেছে, শ্যামলবাবু কোন্ বাড়িতে থাকেন । ছেলেরা ওকে আধঘণ্টা এধার-ওধার ঘুরিয়ে সেই রকের সামনেই হাজির করেছে। লোকের কথা শুনে, সে সত্যি বলছে না মিথ্যে বলছে বোঝা যাবে কী করে—এই ছিল আলোচনার বিষয় ।

সমস্তটা শুনে ঘনাদা বললেন, এ আর এমন কী সমস্যা । সেবার ঘুরতে ঘুরতে প্রশান্ত মহাসাগরের একটা দ্বীপে গিয়ে পৌঁছেচি। পৌঁছনো মাত্র একটা লোক এলো। ফরাসি বোঝে, মোটামুটি বলতেও পারে। তাকেই গাইড করে নিলুম। আগেই জানতুম, এ দ্বীপের বাসিন্দারা অদ্ভুত। যারা সত্যিকথা বলে তারা কখনো সত্যি বই মিথ্যে বলে না, আর যারা মিথ্যুক তারা মরে গেলেও সত্যিকথা বলবে না। গাইডের সঙ্গে এখান ওখান দেখে বেড়াছি। হঠাৎ একটা লোককে দেখে জানতে ইচ্ছে করলো, লোকটা কী জাতের — সত্যিবাদী না মিথ্যেবাদী। লোকটিকে ডেকে জিগেস করলুম। লোকটা দেখলুম ফরাসি বোঝে, কিন্তু কোন্ এক দুর্বোধ্য ভাষায়-না-না, বিনয় করছি না, সত্যিই তার ভাষাটা বুঝতে পারি নি-বললো, গাংহা । গাইডকে বললুম, লোকটা কী বললো হে ? গাইড বললো, ও তো সার বললো হ্যাঁ, কিন্তু লোকটা মিথ্যেবাদী।

তখন আমার খেয়াল হলো, গাইড নিজে কোন্ জাতের সেটাই তো জানা নেই। তবু –

চেয়ের ছেড়ে উঠে ঘনাদা শেষ করলেন, ঠিকই বুঝে নিলুম কে কোন্ জাতের।

ঘনাদার কী বুদ্ধি! কিন্তু কী করে যে বুঝলো!

.

9. শহীদ মক্ষিকা

শেষ পর্যন্ত মাছিটা শহীদ হলো। মরতে তার দুঃখ ছিল না, কিন্তু যা করতে চেয়েছিল তাও করা হলো না । ঝুটমুট প্রাণটা গেলো।

ব্যাপারটা খুলেই বলি। বেণ্ডিলোগাস আর স্টাকামিথিয়া স্টেশন দুটোর দূরত্ব পাক্কা 10 মাইল । নামগুলো জবরদস্ত হলেও স্টেশন দুটো নেহাতই ছোটো, সিংগল লাইনের ট্রেন চলে। একদিন বেণ্ডিলোগাস থেকে একটা ট্রেন ছেড়েছে, চলেচে স্টাকামিথিয়া হয়ে টেরাটোভস্কার দিকে । আর ঠিক সেই একই সময়ে স্টাকামিথিয়া থেকেও একটা ট্রেন ছেড়েছে, চলেচে বেণ্ডিলোগাস হয়ে কাকানো– ফান্টার দিকে। প্রথমটার গতিবেগ ঘণ্টায় 30 মাইল, দ্বিতীয়টার ঘণ্টায় 20 মাইল । প্রথম ট্রেনটার ঈঞ্জিনের ওপর হবুশহীদ মাছিটা বসেছিল। ব্যাপারটা বুঝে দ্বিতীয় ট্রেনটাকে সাবধান করার জন্যে সে উড়লো ঘণ্টায় 300 মাইল বেগে। রেল লাইন ধরে উড়ে সে তাড়াতাড়ি ধরে ফেললো দ্বিতীয় ট্রেনটাকে। এতেই স্টাকামিথিয়ার ড্রাইভারের বোঝা উচিত ছিল। কিন্তু ভ্রূক্ষেপ না-করে সে ট্রেন চালিয়েই চললো। বেচারা মাছি আর কী করে! সে আবার ছুটলো (মানে উড়লো ) প্রথম ট্রেনটার দিকে, একটুও সময় নষ্ট না করে। কিন্তু বেণ্ডিলোগাসের ড্রাইভারও তাকে কোনো পাত্তা দিলো না। মাছিটা আর কী করে। বারবার এ-ট্রেন ও-ট্রেন ছুয়ে বেড়ানো, যদি শেষ মুহূর্তেও ড্রাইভারদুটোর চৈতন্য হয়। কিন্তু কাকস্য পরিবেদনা। বেণ্ডিলোগাস আর স্টাকামিথিয়ার ট্রেনদুটো সোজা মুখোমুখি ধাক্কা মারলো। দুটো এঞ্জিনের মধ্যে পড়ে মাছিটাও শহীদ হলো ।

শহীদ মক্ষিকার সম্মানে ভেবে ছ্যাখো: দুর্ঘটনা এড়াবার জন্য তাকে কতটা পথ ওড়াউড়ি করতে হয়েছিল ?

.

10. ছোট্টো কিন্তু বড়ো সমস্যা

ডক্টর শুশ্রুত কাহালি একজন নামকরা ফিলাটেলিস্ট। রুগীর চিকিৎসা করে তিনি ডাক্তার উপাধি পান নি। যত সব পুরনো ডাক– টিকিটের শুশ্রূষা করেই তাঁর দিন কাটে । এ ব্যাপারে তাঁর জ্ঞান– বুদ্ধিও অগাধ । আমরা ধাঁধা করি শুনে বললেন, ওহে, আমি তো এক ‘ঝামেলায় পড়েছি। আমার অভ্যেস হলো, পাশাপাশি না সেঁটে, একটার তলায় আরেকটা স্ট্যাম্প সাঁটা। সৌদি আরাবিয়ার 1 থেকে 5 রিআল-এর ( ওখানকার মুদ্রার নাম রিআল, আমাদের যেমন রুপি, ইংল্যাণ্ডের পাউণ্ড ) কত যে স্ট্যাম্প পেয়েছি তার ইয়ত্তা নেই ৷ পাতার তলার দিকে দাবার ছকের মতো পাশাপাশি ও লম্বালম্বি চারটে-চারটে করে ষোলোটা ঘর খালি আছে। আমার ইচ্ছে, সব চেয়ে বেশি রিআল-এরটা বেশি ব্যবহার করে স্ট্যাম্প গুলো সাঁটি। কিন্তু কোনো একই দামের স্ট্যাম্প পাশাপাশি বা কোণাকুণি বসাবো না। কিছু একটা উপায় বাতলাও দিকি। আমি চাই, অন্তত 50 রিআল-এর স্ট্যাম্প থাকুক ।

দ্যাখো কী করে করা যায় ।

.

11. তুরুপের রং

ব্রিজ খেলতে বসে মাঝে মাঝে এমন অদ্ভুত তাস হাতে পড়ে যে কহতব্য নয়—বললেন চাম্পিয়ন ব্রিজ-খেলোয়াড় সুগন্ধ চাকলা– নবীশ । তাস-টাস তো ভালো করেই কাটিয়ে দিয়েছি, এক-দুই করে তেরোটা তাস পেলুম। তারপর ভাই সাজাতে গিয়ে দেখি অদ্ভুত কাণ্ড। হাতে চার রঙেরই তাস এয়েছে, প্রত্যেক রঙেরই অন্তত একটা করে তাস আছে, কিন্তু কোনো দুটো রঙের তাসের সংখ্যা এক নয় । আমার হাতে ছিল পাঁচটা রুইতন আর চিঁড়েতন, ছটা হরতন আর রুইতন । আর তুরুপের রঙের ঠিক দুটো তাস। আমরা অবাক হয়ে জিগেস করলুম, তুরুপের রং কী ছিল? চাকলানবীশ মুচকি হেসে বললেন, সেটাই তো ধাঁধা ।

.

12. গয়লার কেরামতি

রামধন গয়লার কারবারই আলাদা। দু-হাতে তিনটে বালতি নিয়ে বীরবিক্রমে চলেচে। দুটো অবশ্য খালি, একটায় 5 সের ভুধ ধরে, অন্যটায় 3 সের। আরেকটা বালতিতে ৪ সের দুধ ধরে– সেটা একেবারে ছাপাছাপি ভর্তি। মা দেখে গালে হাত দিয়ে বললেন, তোমার কাণ্ড দেখে বাপু গা জ্বলে যায়। বাড়িতে জামাই এসচে, একটু পায়েস করবো, আমার 4 সের দুধ চাই। তা এখন দেবে কী করে? তোমার যা হাতের মাপ, ঐ ৪ সের বালতির অর্ধেক কি ঠিক করে দিতে পারবে? রামধন নির্বিকার মুখে বললো, সে আপনি ভাববেন না, মা । এই তিনটে বালতি দিয়েই আপনাকে ঠিক 4 সের দোবো। ঢালা– ঢালিতে কয়েক ফোটা এদিক-ওদিক হতে পারে। কিন্তু সে ধর্তব্যের মধ্যে নয়।

অদ্ভুত রামধনের বুদ্ধি! কী করে ঠিক 4 সের দিলে। বলো তো?

.

13. ভাই ভাই

গণনাথ, হরিশ, পটল, সম্রাট, জোকার আর শিশেবাবু –ছজনেরই পুরনো বই-এর ব্যবসা। সারা ভারত জুড়ে এঁদের লোক লাগানো আছে। কোথায় কোন্ রাজা-রাজড়া বা বড়োমানুষের সংগ্রহ বা পুরনো লাইব্রেরির বই বিক্রি হচ্চে, ঠিক খবর চলে আসে। ব্যস, সঙ্গে সঙ্গে দেখবে হাওড়া স্টেশনে ছ-মূর্তি হাজির। হ্যাঁ, বলতে ভুলে গেচি, এই ছজনের মধ্যে দুজন হচ্চেন র্জাতুতো খুড়তুতো ভাই ।

সেবার বেনারসের গাড়োয়ানতলা লেনে ছ-মূর্তি বই কিনতে গেলেন । যাঁর বই তিনি সাফ বলে দিলেন, দরদস্তুর চলবে না। যা লেনদেন হবে সব পূর্ণ সংখ্যায় । পঞ্চাশ টাকা বললে চল্লিশ টাকা, শেষে চুয়াল্লিশ টাকা তিপান্ন পয়সায় রফা—এসব চলবে না।

ছ-মূর্তি রাজি হলো। গণনাথ কিনলো একটা বই, হরিশ দুটো, পটল তিনটে, সম্রাট চারটে, জোকার পাঁচটা আর শিশেবাবু ছ-টা। এদের মধ্যে যে দুজন র্জাতুতো খুড়তুতো ভাই, তারা প্রত্যেক বই– এর জন্যে সমান দাম দিলো। বাকি চারজনকে প্রত্যেক বইপিছু ঐ দুভাই যা দাম দিয়েছে তার ডবল দাম দিতে হলো। সব মিলিয়ে ছ মূর্তি কিনলো এক হাজার টাকার বই, যদিও সেগুলো তারা বেচবে নিদেনপক্ষে দশ হাজারে।

ধাঁধাটা তাহলে কী? কে কত টাকার বই কিনেচে? আরে না না, সে তো সবাই বলতে পারবে। কথা হল ঐ ছ মূর্তির কোন্ দুজন র্জাতুতো – খুড়তুতো ভাই ?

.

14. ঝিঁঝিপোকার কান্না

প্রথম দিনের খেলা শেষ । থাণ্ডার স্পোর্টিং ক্লাব টসে জিতে– ছিল। টেনিদা পিচ-টিচ দেখে ক্যাবলাকে বললো, মাঠের যা অবস্থা, বল মারাত্মক সুইং করবে। ব্যাট না নেয়াই ভালো । ক্যাবলা প্রতিবাদ করতে যাচ্ছিল, কিন্তু গাঁট্টার কথা ভেবে চেপে গেলো। টেনিদা তো মহা উৎসাহে বল করতে শুরু করলো। হা হতোস্মি। সারাদিন ছোটাছুটি করে, মায় প্যালাকে দিয়ে বল করিয়েও কিছু করা গেলো না। ভ্যাগাবন্ডস ক্লাবের মাত্র তিনটে উইকেট পড়লো। প্রথম দিনের শেষে বিধ্বস্ত টেনিদা আর তার সাঙ্গোপাঙ্গরা বাড়ি ফিরলো।

প্যালার ছোটোকাকার মতো খারাপ লোক আর হয় না । তিনি তাদের অবস্থা দেখে কোথায় সহানুভূতি দ্যাখাবেন, তা না, এক গাল হেসে জিগেস করলেন, কি হে ক্যাবল, ভ্যাগাবন্ডসদের কে সব চেয়ে বেশি রান করলো ? ক্যাবলার এমনিতেই মেজাজ খারাপ হয়ে ছিল । ঘোঁচ মুখ করে বললো:

ওদের ক্যাপটেন আর ভাইস-ক্যাপটেনের রানের যোগফল 109

ওপনারদের রানের যোগফল 114

যে দুজন এখনো খেলচে তাদের রানের যোগফল 108

যে দুজন মনের আনন্দে ক্যাচ তুলে আউট হয়েছে, তাদের রানের যোগফল 115

যে দুজন একই বোলারের বলে আউট হয়েছে, তাদের রানের যোগফল 111

মাত্র দুজন ছক্কা মেরেচে, তাদের রানের যোগফল 110

বল্টুদা আর তার ভাই মিলে রান করেচে 112

আর যে দুটো খেলোয়াড় ওদের টিমে নতুন খেলচে, তারা দুজনে একই রান করেছে। আর ওরাই যে সবচেয়ে কম রান করেচে তা-ও না। এখন বুঝে নিন কে সবচেয়ে বেশি রান করেছে।

ছোটোকাকা তো ঘাবড়ে-মাবড়ে বাড়ির ভেতর চলে গেলেন । এখন তোমরাই একটু হিসেব করে ছোটো কাকাকে তাঁর উত্তরটা দিয়ে দাও ।

.

15. বাঘা দাবাড়ের কাণ্ড

বোড়ে গাঙ্গুলিকে অবশ্য সবাই চেনেন না। কিন্তু অমন একনিষ্ঠ দাবাড়ে বড়ো একটা দেখা যায় না। বিপত্নীক ভদ্রলোক। বাড়িতে আছেন তাঁর এক বোন, এক ছেলে আর এক মেয়ে। চারজনেই বাঘা দাবাড়ে।

বোড়ে গাঙুলি কিন্তু বলেন, আমাদের চারজনের মধ্যেও সেরা খেলোয়াড় ওঁছা খেলোয়াড়ের ব্যাপার আছে। ওঁছা খেলোয়াড় যদি মেয়ে হন তবে সেরা খেলোয়াড়ের যমজ হবেন ছেলে, আর ওঁছা খেলোয়াড় যদি ছেলে হন তবে সেরা খেলোয়াড়ের যমজ হবেন মেয়ে। তবে ভরসার কথা এই যে, সেরা খেলোয়াড় আর ওঁছা খেলোয়াড়ের বয়েস এক। তাহলেই বুঝতে পারছেন, আমাদের মধ্যে সেরা দাবাড়ে কে ।

আমি তো সবজান্তার হাসি হেসে ফিরে এলুম। কিন্তু সেরা দাবাড়েটি তা’লে কে?

.

16. দুধে-জলে

অভ্যেস দূর করা যে কত শক্ত সেটা রামধন গয়লাকে দেখলে বোঝা যায়। দুটো এক আয়তনের বালতি, একটায় রয়েচে এক লিটার দুধ, অন্যটায় এক লিটার জল। ধারে-কাছে কেউ নেই দেখে রামধন চট করে 5 সি. সি. জল নিয়ে দুধের বালতিতে মিশিয়ে দিলো । তারপর মেজোকাকাকে আসতে দেখে সেই জল-মেশানো দুধ থেকে 5 সি. সি. নিয়ে জলের বালতিতে ঢেলে দিলো ।

এখন রামধন ভাবচে জলের বালতিতে দুধের পরিমাণ বেশি, না দুধের বালতিতে জলের পরিমাণ বেশি। পাঠকের কী মত?

17. প্রচ্ছন্ন পাটীগণিত

গোদাবরীর তীরে, সেই বিখ্যাত শাম্মলী তরুর ছায়ায় ধুনি জ্বালিয়ে বসে থাকেন এক মৌনীবাবা। ছটু একদিন তাঁকে জিগেস করলো, আচ্ছা, আপনি কতবার এপার-ওপার করেছেন? মৌনীবাবা কাঠকয়লা দিয়ে লিখে দিলেন:1129. ছটু ভাবলো, বাব্বা, এক হাজার একশ ঊনতিরিশ বার নদী পার হওয়া কি চাট্টিখানি কথা? আসলে কিন্তু মৌনীবাবা লিখেছিলেন: একবারো নয় !

অক্ষরের বদলে সংখ্যা লিখে গোপন খবর পাঠাবার ব্যবস্থা অনেক দিনের পুরনো। এর নাম হলো cryptography বা প্রচ্ছন্ন– লিপি। এরও আবার হাজারো কৌশল আচে। আসল কথা বার করতে এক-একবার এক-এক রকম কায়দা কাজে লাগাতে হয় ।

প্রচ্ছন্ন পাটীগণিত বা cryptarithmetic হলো এরই উলটো। সংখ্যার বদলে অক্ষর লিখে অংক করা ।

ক্রিপ্টেরিথমেটিক নাম দিয়ে ব্যাপারটা চালু করেছিলেন ‘মাইনোস‘ ছদ্মনামের আড়ালে প্রচ্ছন্ন বেঁধেল এম. ভাত্রিক্যাৎ । “স্ফিংক্স” নামে বেলজিঅম-এর এক মজার অংক পত্রিকায় ব্যাপারটা প্রথম বেরোয় ( মে, 1931 ) ।

ব্যাপারটা দাড়ায় এই র’ম : বাবা + সিসি = মাসিমা ।

যোগফলটা মেলাতে গেলে ‘মা‘ হবে 1, কারণ ছু অংকের জুটি রাশির যোগফল যদি তিন অংকের হয় তবে যোগফলের শতকের ঘরের অংকটি 1 ছাড়া আর কিছুই হতে পারে না । ‘বা‘ আর ‘সি‘

0 হতে পারে না । সুতরাং ‘বা আর ‘সি’র যোগফল হবে 11 ; তাহলে ‘বা’+ ‘সি‘ + হাতে 1-এর যোগফল দাঁড়ায় 12. অতএব ‘সি‘ = 2, ‘বা‘ = 9, অর্থাৎ, বাবা + সিসি = মাসিমা মানে 99 +22 = 121.

বলে রাখা ভালো, এর কোনো সূত্র বা ফর্মুলা নেই । বুদ্ধি খাটিয়ে, লেগে থেকে অক্ষর ভেঙে অংক বার করতে হয়। তবে এই পাটীগণিত করতে থাকলে কয়েকটা সাধারণ নিয়ম পাওয়া যাবে। এখন দুটো সমস্যা দেয়া যাক। সমাধান করো:

.

  অ ম ল

  ধ ব ল

জ ল জ ক ল ম

+ ক ম ল                X ক ল ম

_ __________ ________

ঝ ল ম ল হ য ব র ল

.

18. বন্দী পতঙ্গ

রোজ রাত্তিরে এক কাপ হরলিকস খাওয়া টিপুবাবুর অনেক দিনের অভ্যেস। তাঁর ছেলে টিফুর ‘হবি‘ হলো পোকামাকড় জোগাড় করে সেই খালি হরলিকসের বোতলগুলোর ভরে রাখা। একদিন দুটো অদ্ভুত পোকা পেয়ে দুটো খালি বোতলে রাখতে গেলো । হঠাৎ কী ভেবে চোখ বড়ো বড়ো করে দাড়িয়ে রইলো ।

ব্যাপারটা কী ? টিফু বললো, দেখুন, ছটো বোতলই যদি পাল্লায় চাপাই, একই ওজন হবে । এবার দুটোরই ঢাকনা খুলে ঢাকনা দুটো পাল্লাতেই রাখলুম। পোকাদুটো বোতলের গায়ে বা তলায় বসলো না, বোতলের মধ্যেই উড়ে বেড়াতে থাকলো । তখন একটা বোতলের ঢাকনা তুলে সেটা বন্ধ করে দিলুম। অন্যটা যেমন ছিল তেমনিই রইল। এখন দুটো বোতলের ওজনে কিছু কমবেশি হবে কি ?

কী আর করি। আমিও গালে দিয়ে ভাবতে বসে গেলুম।

.

.

19. ঘনরাম দাসের দিনপঞ্জি থেকে

না তথ্য তস্থ্য । ঘনাদার সেই পূর্বপুরুষ, যিনি কর্তেজ-পিজারোর সঙ্গে মেক্সিকো-পেরু ঘুরে বেড়িয়েছিলেন। তাঁরই দিনপঞ্জিতে এই আশ্চর্য ঘটনাটি লেখা আচে। সেটাই ছেপে দিচ্চি:

31 ডিসেম্বর, 1499 – আলমিরান্তে দন ক্রিস্তোবাল কোলোন ( অর্থাৎ ক্রিস্টফার কলম্বাস ) মার্গারিতা দ্বীপে সাতিশয় মাৰ্জ্জিত এক রাজন্যের সহিত মিলিত হইলেন । হিসপানিওলার আদিম মানবগণ তাঁহাকে দর্শন করত যদ্রূপ ধূলিলুণ্ঠিত হইয়া প্রণতি জানাইয়াছিল, এই রাজন্য ও তাঁহার অনুচরবর্গ তদ্রূপ কিছুই করিলেন না। শুদ্ধ ইঙ্গিতে জানাইলেন, তাঁহারা আলমিরান্তের জন্যই অপেক্ষমাণ। আলমিরাতে তাঁহার সহিত এক মহাশৈলের অভ্যন্তরে প্রবিষ্ট হইলেন। কাঞ্চনকামী কোলোন বিমূঢ়। এক সুবৃহৎ নগরী সেই দুরধিগম্য গুহার শোভা, তাহার প্রতিটি ইষ্টক সুবর্ণনিৰ্ম্মিত! সূর্যকিরণ সেই মহাতিমিরে প্রবেশাধিকার লভে নাই । তত্রাচ ঐ হৈমনগরা চিরসন্দীপ্তিমান। অভিভূত আলমিরান্তে প্রশ্ন করিলেন, এই নগরী কত প্রাচীনা? উত্তরে রাজন্য কহিলেন, এই অরুণাদিত্যপুরী মহাকালের অৰ্দ্ধবয়স্ক। অযুত বৎসর পূর্ব্বে এই নগরীর যাহা বয়স ছিল তাহা অদ্য হইতে অযুত বৎসর পর মহাকালের বয়স যাহা হইবে তাহার ত্রি-অষ্টমাংশ। সুতরাং বিবেচনা করুন এই নগরী কত প্রাচীনা । দন ক্রিস্তোবাস বাক্য নিঃসরণ করিতে অপারঙ্গম হইলেন । তাঁহার চেতনা ধীরে? প্ৰলুপ্ত হইল ৷ বহু দণ্ড অতিক্রান্ত হইলে পর সহসা আবিষ্কার করিলেন তিনি বালার্করাগরঞ্জিত বিজন বালুতটে শয়ান। সেই মহাশৈলের কোনো সন্ধান অদ্যাপি মিলে নাই । সকলেই আল– মিরাস্তেকে কিঞ্চিদধিক উপহাস করিতেছে। আমি কিন্তু তাঁহাকে বিশ্বাস করিয়াছি।

ঘনরাম দাস সে মায়াপুরীর খোঁজ পেয়েছিলেন কিনা জানি না । আমাদের সমস্যা হলো : সে শহরের বয়েস এখন তাহলে কত হবে?

.

20. আপত্তিকর চিঠিচাপাটি

আমাদের ‘ধাঁধা‘ পত্রিকার দপ্তরে নানা ধরনের চিঠি আসে ৷ বেশির ভাগই গদ্যে, মাঝে মাঝে পদ্যে । প্রথম-প্রথম পদ্যে চিঠি পেলে ভালোই লাগতো। এই যেমন সেদিন একটা এলো :

‘ধাঁধা‘ অতি খাসা কাগজ

ধাক্কা খেলুম নিম-এর বেলায়

অংক কষার ব্যাপার আছে

তিন-পাঁচ-সাত কাঠির খেলায়!

বার কয়েক তো হেরেই গেলুম,

জেতার এখন উপায়টি কী?

কায়দাটুকু জানার জন্যে

গচ্চা গেলো তিনটি সিকি । ইতি

জগমোহন দাঁ ।

আমাদের সম্পাদক তো রেগে কাঁই। তক্ষুনি খসখস করে লিখে

ফেললেন:

ওহে বাপু জগমোহন

তোমার ঘিলু করলে দোহন,

গাদা খানেক গোবর পাবে,

ধার করা তাও! শুখবে কবে ?

তারপর আমাদের দিকে তাকিয়ে বললেন, কেমন দিলুম ?

আমরা তো হাঁ ! বলে কি ! অমন চমৎকার ছড়ার জবাবে এ র’ম সাংঘাতিক ছররা! সম্পাদক তখন মুখ টমেটো করে বললেন,

আদ্যক্ষরী গালাগাল — অসহ্য !

ব্যাপারটা তখন বোঝা গেলো। চিঠিটার প্রত্যেক চরণের প্রথম অক্ষরগুলো ওপর থেকে নীচে পড়ে যাও—সত্যিই সম্পাদকের চটে যাওয়ার কারণ আছে। তাই বলে দাঁবাবুকে গাধা বলাটা কি উচিত হলো?

আদ্যক্ষরী বা Acrostic ব্যাপারটা কবিতার কারিকুরির ইতিহাসে অনেক দিনের পুরনো। হিব্রু ধর্মগ্রন্থে, বাইবেলের পুরাতন নিয়ম বলে যা চালু, বহু জায়গায়, যেমন, ‘বিলাপগ্রন্থে’র প্রথম চারটি কবিতায়, ‘প্রবাদমালা’র 31নং কবিতায়, রাজা দায়ুদের 19নং গীতে হিব্রু বর্ণমালার আলেফ থেকে তাউ পর্যন্ত বাইশটি বর্ণ ওপর থেকে নীচে সাজানো আছে। ইংরিজিতেও এমন অনেক কবিতা পাওয়া যায়। বিখ্যাত হলো কিট্স-এর Give me your patience, sister, while I frame, যার প্রত্যেকটি চরণের প্রথম অক্ষর জুড়ে কবির বোন জর্জিআনা অগাস্টা কিট্স-এর নাম পাওয়া যায়। “আজব দেশে অ্যালিস”-খ্যাত লিউইস ক্যারল “আয়নার মধ্যে দিয়ে” (Through the Looking Glass ) বইটির শেষ কবিতায় আদ্যক্ষর সাজিয়ে অ্যালিস-এর আসল নামটি লিখে দিয়েছেন।

বাংলাতেও এককালে এর বেশ চর্চা ছিল। ঈশ্বর গুপ্তকে গালা– গাল দিয়ে একটা আদ্যক্ষরী লিখেছিলেন “দুর্জনদমন মহানবমী” পত্রিকা ( বিনয় ঘোষ, “বিদ্যাসাগর ও বাঙালী সমাজ,” কলকাতা : ওরিয়েন্ট লংম্যান, কবিতাটি বেশ সরল ঈশ্বর–

বন্দনা, কিন্তু আদ্যক্ষর ধরে পড়ে চললে বড়োই খারাপ কথা । মধুসূদন যখন হিন্দু কলেজে পড়তেন তখন তিনি কবিতা লিখতেন ইংরিজিতেই, কিন্তু এমন অন্তত একটা বাংলা কবিতা পাওয়া গ্যাছে ( ‘বর্ষাকাল’ ) যার আদ্যক্ষর পড়লে তাঁর বাল্যবন্ধু গৌরদাস বসাকের নাম পাওয়া যায় ( মধুসূদন রচনাবলী, কলকাতা : হরফ প্রকাশনী, নজরুল ইসলামও স্কুলে পড়তে এক মাস্টারমশায়ের বিদায় উপলক্ষ্যে একটা আদ্যক্ষরী লিখেছিলেন। তার কায়দাটা একটু আলাদা । প্রত্যেক স্তবকের প্রথম চরণের প্রথম অক্ষরে নিজের নামের এক-একটা অক্ষর রয়েছে (খান মইনুদ্দীন, “যুগস্রষ্টা নজরুল, ‘ কলকাতা : হরফ প্রকাশনী, 1377 বঙ্গাব্দ, পৃ 13-16 দ্র)।

পরে অবশ্য আদ্যক্ষরী ব্যাপারটা খানিক খাপছাড়া চেহার ! নিয়েছে। আক্রিস্টিক-এর মধ্যে মধ্যাক্ষরী বা অন্তাক্ষরীও ঢুকে গ্যাচে। ওপর-নীচ দুভাবে পড়া যায়—এমন কবিতা লেখা হয়েছে। কবিতা হিসেবে সব সময় যে ভালো হয়েছে তা নয়, তবে কৌশলটাও তো দেখার জিনিস ।

আদ্যক্ষরীর আসল মজাটা কোথায়? কবি তো যা হোক করে অক্ষরগুলো সাজিয়ে, মুখ-টখ মুছে, দিব্যি ভালোমানুষ সেজে বসে থাকলেন। পাঠক এখন সেটা ধরতে পারলো কিনা—-এই হলো সমস্যা। না পারলে অবশ্য খুব ঝামেলা। যেমন আমাদেরই হয়েছিল। এই তো সেদিন একটা চিঠি এলো—

.

আপসে লোকে প্রণাম করবে,

নারাজ লোকও হারাজ হবে ঠিক,

এতই চালক মানুষ ধাঁধাড়ুৱা–

বোকায় মানে খোঁজে চতুর্দিক ।

.

আমাদের সম্পাদক চটে গিয়ে উত্তর পাঠালেন, তোমার মতো নয় ।

আমাদেরই এক বন্ধুকে গ্রাহক হতে বলে পত্রিকার প্রথম সংখ্যাটা উপহার পাঠিয়েছিলুম। বন্ধু চিঠি লিখে জানালো :

ধাঁধার পরের সংখ্যা আবার কবে পাওয়া যাবে?

ধারণা করতে পারবে না, প্রথম সংখ্যা পেয়ে গৃহ

কপোতের মতো আনন্দে বকবকম করে উঠেছিল বন্ধ

বেতালা মনটা। বলছ যখন, নিশ্চয়ই গ্রাহক হব ।

কোথায় নতুন গ্রাহক পেয়ে খুশি হবে, তা না, সম্পাদক চটে উঠে বললেন, লিখে দে, ধাঁধা চলচে — চলবে।

কিন্তু ব্যাপারটা খুব গুরুতর হয়ে দাড়ালো গত তরশু। চিঠি এলো:

ধাঁধা করতে যেই বসেচি কাগজ-কলম সব সাজিয়ে

বাধা পড়লো সঙ্গে সঙ্গে। হাজির হলো বেল বাজিয়ে

সরেস যত পাড়ার ছেলে, বদবুদ্ধি ভর্তি মগজ,

বলে ‘চম্পাহাটী চলুন, কত নেবে টেরিন ছ-গঞ্জ ?‘

কত টাকা দক্ষিণা তার জানব আমি কেমন করে ?

কাপড়-জামা কেনার সময় ঠিক নিয়ে যায় আমায় ধরে।

বলবে ওরা, ‘দর কমাতে আপনি ছাড়া পারবে বা কে ?

কেই বা জানে কোন্ মুলুকে সময়ের দাম পড়তে থাকে ?

কোথায় থাকে হীরু কুণ্ডু, কোথায় লণ্ডী পৈতে কাচার

কোথায় পাব খুব ভালো চা, মুড়ির সঙ্গে তেলের আচার ?

আমার তো ভাই চিরদিনই ধাঁধা করতে দারুণ ইচ্ছে,

কিন্তু সময় পাচ্চি না যে, পাড়ার লোকে বাধা দিচ্চে।

.

সম্পাদক চিঠিটা একবার পড়লেন, দুবার পড়লেন, তারপর হেড অপিসের বড়োবাবুর মতো আঁতকে উঠে নিজেই পড়ে গেলেন। জ্ঞান হারানোর আগের মুহূর্তে শুধু হেঁচকি তুলতে তুলতে বললেন, থানায় খবর দে, লোকটার নাম শেষ লাইনে লেখা আছে। তাঁর এই অবিমৃষ্যকারিতায় আমরা তো কিংকর্তব্যবিমূঢ়।

21. বাটপাড়িয়া হত্যা রহস্য

বিখ্যাত নিরক্ষর ধনকুবের দৌলতরাম বাটপাড়িয়ার মৃত্যু রহস্য শেষ পর্যন্ত রহস্যময়ই রয়ে গেলো ।

তদন্তের কোনো ‘ত্রুটি‘ ছিল না। পায়ের ছাপটা যে মেক্সিকোর কোনো ইনকা-র, তার অকাট্য প্রমাণ ছিল। ঘটনাচক্রে যা ঘটা স্বাভাবিক, অর্থাৎ হত্যাকারীর পকেট থেকে তুলোট কাগজে লেখা এক টুকরো ‘কিপু’ও মৃতদেহের পাশে পড়ে ছিল। আর পুরো ব্যাপারটাই যে একটা বিরাট আন্তর্জাতিক ষড়যন্ত্রের অংশ তা নিয়েও কোনো সন্দেহ বা সংশয় ছিল না।

মুশকিল হয়েছিল অন্য জায়গায় ৷ এ সমস্ত ক্ষেত্রে সচরাচর যা ঘটে থাকে, সেগুলোর কোনোটাই দৌলতবাবুর বেলায় খাটে না। এক নম্বর, হত্যার সময় বাড়িতে চাকর-বাকর ছাড়া আর কোনো জনপ্রাণী না থাকাই নিয়ম ( খুব বেশি হলে একজন অতিবৃদ্ধা কালা পিসি থাকতে পারেন)। কিন্তু দৌলতবাবুর আত্মীয়-স্বজন অতিথি– পরিজন মিলে বাড়িটা ছিল ফোর্ট উইলিঅম-এর মিনি সংস্করণ। তারা সব্বাই রাত দশটায় দৌলতবাবুর আর্তনাদ শুনেচে। কিন্তু দৌলতবাবু আরশোলা দেখলেও ঐ একই রকম চিল-চিৎকার করতেন, তাই কেউ বিশেষ গা করে নি । একমাত্র তাঁর নিজস্ব চাকর সাগর ছুটে গেলো । সে শুধু দৌলতবাবুকে গুলিবিদ্ধ অবস্থায় পড়ে থাকতে দেখেচে, আর কিছু দ্যাখে নি। ফলে দুনম্বর মুশকিল হয়েছে সেই ছোকরাকে নিয়ে। নিহত ব্যক্তির ভৃত্য বহু পুরাতন এবং বিশ্বস্ত হওয়ার কথা। কিন্তু সাগর মাত্র দিনকুড়ি হলো

কাজে ঢুকেছে, আর দিনদশেক বাদেই তার চাকরি চলে যাওয়ার কথা ।

চার নম্বর মুশকিল এইখানেই । এ বাড়ির সকলেই দৌলতবাবুর ওপর চটা ছিল। সকলেই বলছে, সময়-সুযোগ হলে তারাই দৌলত– বাবুকে খতম করতো, শুধু অন্য কে যেন সেটা করে দিয়ে গ্যাছে।

সুতরাং হত্যার উদ্দেশ্য বা মোটিভ ধরে কিছু ঠিক করতে গেলে কাঁকর বাছতে কুলো উজাড় হওয়ার অবস্থা।

গোয়েন্দা টিকেকাশি (ইনি হুঁকোকাশির ভায়রাভাই কল্কেকাশির ভায়রাভাই) অবশ্য ‘কিপু‘ পড়ার জন্যে কিউবা-র কনস্যুলেট অপিসে যেতে চেয়েছিলেন। রামধমক দিয়ে সবাই তাঁকে থামিয়ে দিলো । তিনি কিন্তু বাটপাড়িয়া হত্যা রহস্যের ব্যাপারে লেগে রইলেন। ‘কিপু’র কাগজটা উলটে পালটে দেখে তো তাঁর চক্ষুস্থির। কিপু না ছাই, একটা সংখ্যা-লেখা কাগজ, ওড়িয়ায় লেখা 227187.

প্রথমে মনে হলো নির্ঘাত টাকার হিসেব। একটু ভেবে তিনি এর সংখ্যামূল নির্ণয় করলেন । তারপর ঘাড় দোলাতে দোলাতে বললেন, হুঁ হুঁ । যা ভেবেচি তাই। চারজন মিলে একাজ করেছে। এই সংখ্যামূল থেকেই তো ধরা পড়ে গেলে চাঁদ । এবার হাতকড়া পরালেই হয়। স্পষ্ট বুঝতে পারছি, একজন আগে থাকতে ঘরে ঢুকেছিল, আরেকজন কেশনগর থেকে আরশোলা কিনে এনেছিল, আরো একজন ইনকাম ট্যাক্স অফিসর সেজেছিল, আর ঐ ছোকরা চাকর ছুরিটা সমূলে বসিয়ে দিয়েছে। দৌলতবাবু ঘরে লোক দেখে প্রথমেই চমকে উঠেছিলেন, তার পরেই দেয়ালে আরশোলা দেখে আর্তনাদ, ইনকাম ট্যাক্স ইন্‌সপেক্টরকে দেখে বাকরোধ, আর সাগরও সেই সুযোগে—। নাক দিয়ে একটা আওয়াজ করে টিকেকাশি বললেন, হয়েছে।

কিন্তু প্রমাণ কোথায়? ঘরে কোনো আরশোলা পাওয়া যায় নি । সাগরের প্রধান কাজ ছিল রোজ সকাল-সন্ধে আরশোলা খুঁজে খুঁজে মারা। অবশ্য একটা টিকটিকি ছিল বলে শোনা গ্যাচে। টিকেকাশি বললেন, এলিমেন্টারি, মাই ডিআর। ঐ টিকটিকিটাই আরশোলাটাকে খেয়ে ফেলেচে। বাকি দুজন লোক গেলো কোথায়? টিকেকাশির নিশ্চিত ধারণা, ওরা নিশ্চয়ই বাড়ির ভেতরের লোক, সুতরাং তাদের ঢোকা ও বেরোনোর কোনো অসুবিধেই ছিল না ৷

পুলিস কমিশনার মিস্টার দাশগুপ্ত ঘাড় নেড়ে স্বীকার করলেন, তা সম্ভব । কিন্তু এত কথা টিকেকাশি জানলেন কী করে ?মৌরি হেসে টিকে কাশি ‘কিপু’র কাগজটা বাড়িয়ে দিলেন । কমিশনার ঢোক গিলে বললেন, এতো আমার ফোন নাম্বার মশাই, এর থেকে আবার কী বেরোবে ? উনি বোধহয় আমায় ফোন করেছিলেন। জানেনই তো, আমার ফোন– আওয়ার সকাল পৌনে ন-টা থেকে সোয়া ন-টা।

টিকেকাশি শুকনো মুখে বেরিয়ে এলেন। জীবনে কোনোদিন তাঁর এত অপমান হয় নি। সোজা বাড়ি গিয়ে ঠিক করলেন, আর গোয়েন্দাগিরি নয় । এখন থেকে তিনি সেরেফ অংক করবেন। গোড়া থেকে শুরু করাই ভালো, তাই ভাইঝির কাছ থেকে একটা ধারাপাত চেয়ে নিয়ে ঘরের দরজা বন্ধ করে দিলেন। ঘণ্টা চারেক বাদে তাঁকে আবার উত্তেজিত অবস্থায় কমিশনারের দপ্তরে দেখা গেলো।

কমিশনার অবশ্য ভদ্রতার ত্রুটি করলেন না। চা-টা খাইয়ে টিকেকাশির বক্তব্য শুনে বললেন, কী নাম বলছেন ?

পক্ষ পক্ষ ঋষি চন্দ্র বসু ঋষি ? না মশাই, ও র’ম নামের কোনো কুখ্যাত খুনী বা খুনীগণ আছে বলে মনে হয় না । মানে, ইন্টারপোল-এ থাকতে পারে, আমাদের জানা নেই । তাছাড়া নামতা থেকে নাম পাওয়া যেতে পারে, তাই বলে টেলিফোন নাম্বার থেকে নাম বার করবেন ? টিকেকাশি অনেক করে তাঁকে বোঝালেন, না হলে ঐ কাগজটা পড়ে থাকার কোনো মানে হয় না। কিন্তু মিস্টার সেনগুপ্ত বেল বাজিয়ে পরের লোককে আসতে বললেন ।

কয়েক বছর পরের কথা। টিকেকাশি এখন সেরেফ ভাষাতত্ত্ব চর্চা করেন। হঠাৎ সকালে কাগজ পড়ে লাফিয়ে উঠলেন। সাগর বসু ওরফে ব্রহ্মর্ষি (দেখতে ভিজে বেড়ালটি ছিল বলে বাচ্চা বয়েস থেকেই বন্ধুরা ঐ বলে খ্যাপাতে।) গতকাল সমগ্র অপরাধীজগৎকে চোখের ঐ জলে ভাসিয়ে সাধনোচিত ধামে প্রস্থান করেছেন। সাগর বসু ওরফে ব্রহ্মর্ষি!! টিকেকাশি যেন 440 ভোল্টের শক খেলেন। সাগর মানে সিন্ধু মানে 7, বসু মানে ৪, ব্রহ্ম মানে 1, ঋষি মানেও 7. হায় হায়, তখন যদি ধারাপাত না পড়ে “ভাষার ইতিবৃত্ত”টা পড়তেন! কবিশকাব্দের কায়দায় গৌরববাবু তো খুনীর নামটাই লিখে গেলেন, শুধু একটু ভুলের জন্যে–! সাতে যে ঋষি সাগর দুইই হয়, একে চন্দ্র আর ব্রহ্ম!

ভুল একটা নয় । পুরো গল্পটাই ভুলে ভরা। তথ্য আর বর্ণনায় এ-র’ম কত ভুল আছে, পাঠক কি খুঁজে বার করবে?

22. যাদুবর্গ ও বিযাদুবর্গ

যাদুবর্গ (magic square) ব্যাপারটা এতই চালু যে কাউকে বোঝাতে গেলেই বিরক্ত হবে। 1 থেকে শুরু করে বর্গের মতো সাজানো পূর্ণ সংখ্যা, যার প্রত্যেক সারির ওপরে-নীচে, পাশাপাশি এবং প্রধান দুটি কর্ণ যোগ করলে একই যোগফল পাওয়া যাবে । ব্যাপারটা এতই চমৎকার যে, লোকে লকেট করে যাদুবর্গ গলায় পরে, আংটি করে হাতে রাখে। যাদুবর্গ তৈরির কৌশল নিয়ে এককালে অনেক হৈচৈ হয়েছে, ভল্যুম ভল্যুম বই বেরিয়েছে।

দু ঘরের যাদুবর্গ তো সম্ভব নয়, অন্তত তিন ঘরের হতেই হবে। তিন ঘরের যাদুবর্গের (1 থেকে 9 অবধি ব্যবহার করে) সব দিকের যোগফল হবে 15, চার ঘরের 34. পাঁচ ঘরের বা ছ ঘরের যাদুবর্গের যোগফল তাহলে কত হবে? এর কোনো সাধারণ সূত্র বার করতে পারো?

যাদুবর্গের সংখ্যাগুলো 1 থেকেই শুরু করতে হবে এমন কোনো কথা নেই। 2 বা 3 বা আরো বড়ো সংখ্যা থেকে শুরু করে পরপর আটটা বা পনেরোটা বা চব্বিশটা সংখ্যা নিয়েও যাদুবর্গ সাজানো যায়। এমন কিছু শক্ত ব্যাপার নয়, কিন্তু এখানেও একটা প্রশ্ন আছে। 1 থেকে শুরু না করে যদি অন্য কোনো সংখ্যা দিয়ে শুরু করি, তাহলে তিন ঘরের যাদুবর্গ সাজানোর সাধারণ সূত্রটা কী হবে?

শুধু জোড় বা বিজোড় সংখ্যা দিয়ে চমৎকার যাদুবর্গ সাজানো যায় ৷ প্রথম ন-টি বিজোড় সংখ্যা 1, 3,.., 15, 17 দিয়ে তিন ঘরের বর্গের একটা নমুনা দিচ্চি:

7	5	15
17	9	1
3	13	11

.

যাদুবর্গের খোঁজ সবাই রাখে। কিন্তু বিযাদুবর্গ (anti-magic square)? যাদুবর্গের ঠিক উল্টো হলো বিযাদুবর্গ ।

সংখ্যাগুলো এমন ভাবে সাজাতে হবে যে ওপরে-নীচে, পাশাপাশি আর প্রধান ছুটি কর্ণ যোগ করলে কখনো এক যোগফল হবে না। শুনলে মনে হয়, এ আর এমন কি । সব দিকের যোগফল এক করাটাই সমস্যা। বিষম যোগফল তো হামেশাই বেরোবে। একবার করতে চেষ্টা করো. বুঝবে আটটা আলাদা যোগফল করতেও এলেম লাগে । দু-চারটে যোগফল কেমন যেন বিশ্বাসঘাতকতা করে এক হয়ে যায় ।

একটা বিযাদুবর্গের নমুনা দি:

1 থেকে 9 অবধি সংখ্যাগুলো পরপর সর্পিল (spiral) আকারে সাজানো হয়েছে। দাবা খেলার নৌকোকে 1 থেকে চালাতে শুরু করলে ঠিক আইনমাফিক 9-এ গিয়ে পৌঁছবে। এর যে-কোনো সারির ও প্রধান দুটি কর্ণের (1-9-5, 3-9-7) যোগফল বিষম ।

এ ছাড়া আর কোনো ভাবে তিন ঘরের বিষাদুবর্গ সাজাতে পারো? যাদুবর্গের মতো বিযাদুবর্গের ধরনও নেহাত কম না ৷

একই বিযাদুবর্গকে ঘুরিয়ে বা আয়নার সামনে ধরে যে বর্গ পাওয়া যাবে, সেগুলো কিন্তু আলাদা বলে ধরা হবে না।

.

23. পায়ে ধরে সাধা

গুপ্তধনের নেশা ডিটেকটিভ বইএর চেয়েও মারাত্মক। মৃত্যুঞ্জয় নাকে-কানে খৎ দিয়ে বলেছিল, আর কোনদিন গুপ্তধনের লোভ করবে না। কিন্তু মনটা কেমন যেন খুঁৎ খুঁৎ করতে থাকে। আর কপালও তেমনি। একদিন রাগোধাল গ্রামে পৌঁছে দ্যাখে, সারা গ্রামের লোক গালে হাত দিয়ে বসে আছে। গ্রামের সব জমি আল দিয়ে আলাদা করা, তবে প্রত্যেক জোতই লম্বায়-চওড়ায় সমান । এর কোনো একটা জোতে বিশে ডাকাতের গুপ্তধন পোঁতা আছে— জোতটার তিনটে কোণ থেকে 2, 3 আর 4 মিটার দূরে। এখন কোন্ জোতটা যে বিশে ডাকাতের পছন্দ হয়েছিল, সেইটাই কেউ জানে না। আর হ্যাঁ, বলতে ভুলেই যাচ্ছিলুম, প্রত্যেক জোতই লম্বায়-চওড়ায় সমান, কিন্তু কোনো দুটো জোতই সমান লম্বা নয়।

মৃত্যুঞ্জয় গোটা ব্যাপারটা শুনলো। মুদির কাছ থেকে এক টুকরো খড়ি নিয়ে কী যেন আঁক কষলো। তারপর কোদাল দিয়ে একটা জোত কোপাতে শুরু করলো । সারা গ্রাম, মায় বেড়াল কুকুরগুলোও, নিঃশ্বাস বন্ধ করে দাঁড়িয়ে আছে। মৃত্যুঞ্জয় কপালের ঘাম পুঁছলো। মাটি আর কেঁচো ছাড়া আর কিছুই ওঠে নি। চাপা হাসির আওয়াজের মধ্যে মৃত্যুঞ্জয় সেই জোতেরই আরেক দিকে কোদাল চালালো । খুকখুক আওয়াজ ছাপিয়ে শব্দ উঠলো—ঠং! ঘড়া ঘড়া মোহর: ভাগ্যবানের বোঝা, কথায় বলে, ভগবানে বয় । আটবারের জায়গায় মাত্র দু বার খুঁড়েই গুপ্তধন পাওয়া গেলো । কোন্ জমিতে বিশে ডাকাত মোহর পুঁতেছিল, মৃত্যুঞ্জয় সেটা বুঝলো কী করে?

.

24. দস্তুরমতো দরদস্তুর

সমর ধাড়াকে মনে আছে নিশ্চয়ই। সেই যে সেবার আমাদের সম্পাদকের মুণ্ডু চাই বলে ভয় দেখিয়ে চিঠি দিয়েছিল। ভদ্দরলোককে ( যদি ও-র’ম বিপজ্জনক লোককে আদৌ ভদ্দরলোক বলা যায়!) কেন ছেলেরা বাজার যাওয়ার সময় টানাটানি করে, তা সেদিন স্পষ্ট বুঝতে পারলুম । সেবার সারা পাড়া উজাড় করে সব পিকনিক করতে যাবে, ধাড়া মশায়ের দায়িত্ব পড়লো ডিম কেনার। গলদঘর্ম হয়ে ফেরার পর সবাই তাঁকে ঘিরে বললো, কত সস্তায় কিনলেন দাদা? ধাড়া মশায় ঠাণ্ডা গলায় বললেন, তা শ-এ এক টাকা কমিয়েচি। ব্যাপারটা কেউই বুঝতে পারলো না । ধাড়া মশাইও তেমনি, যেন খুব বুঝিয়ে বলচেন এমন ভাব করে বললেন, তিরিশ টাকার মাল কিনে পাঁচটা বেশি হলে। আর কি।

মাথামুণ্ডু কিছুই বুঝলুম না । তোমরা কিছু বুঝলে?

.

25. খলট অ্যাভিনিউ-এর ডাকপিয়ন

কার্ল গাউস ( 1777–1855 ) তখন পাঠশালায় পড়ে, বয়েস আট । গুরুমশায়ের বোধহয় বাইরে যাবার দরকার ছিল : তিনি বললেন, ছেলেরা শোনো। 1 থেকে 100 অবধি যোগ করে দেখ যোগফল’টা কত হয়। একবার হয়ে গেলে রিভাইস করবে। ছেলেরা তো দুই আর একে তিন, তিন আর তিনে ছয়-এই করে হিসেব করচে। কার্ল মহা ধুরন্ধর ছেলে, তার নজর পড়লো, 1 আর 100, 2 আর 99, 3 আর 98–এই ভাবে যোগ করলে 50 আর 51 পর্যন্ত পৌঁছে সব ক-টারই যোগফল হয় 101. তাহলে যোগফলটা নিশ্চয়ই নিশ্চয়ই হবে 50×101 = 5050. শোনা যায়, গুরুমশাই নিজেও জানতেন না, 1 থেকে 100 যোগ করলে কত হয়। ফলে, তাঁকে আবার যোগ করে দেখতে হলো কার্ল-এর উত্তরটা ঠিক হয়েছে কিনা। গাউস-এর কায়দাটা কী ছিল ? এইভাবে লিখলে বুঝতে আরো সুবিধে হবে।

S= 1+ 2+ 3+…+1০০

S=100+99+98+…+1

2S=100 (101)

S= $\frac{100(1+100)}{2}$

এখন যদি প্রথম সংখ্যাটা a, শেষ সংখ্যাটা, l আর এই শ্রেণীতে মোট যতগুলো সংখ্যা আছে (1 থেকে 100 মানে 100 টা সংখ্যা )

তাকে n ধরি, তাহলে সূত্রটা দাড়ায় : S = $\frac{n(a+l)}{2}$

S=n (a+1)

সূত্রটা যে কেবল স্বাভাবিক সংখ্যা, অর্থাৎ 1, 2, 3, 4, ইত্যাদি, যেখানে প্রত্যেক সংখ্যা তার আগের সংখ্যার চেয়ে 1 বেশি, তার ক্ষেত্রেই খাটবে এমন নয়। 4, 8, 12, 16, 32 এ-র’ম শ্রেণীর যোগফল ও বার করা যাবে । এর বেলায় যোগফল হবে

8(4+32)

2

= 144.

4 আর-8, 8 আর 12, 12 আর 16 – এদের সবার মধ্যেকার তফাৎ হলো 4. তাহলে 32-এর ঠিক আগে, এই শ্রেণীর সপ্তম সংখ্যা তবে 28. আর 32-এর পরেও যদি এই শ্রেণীটা বাড়তে থাকে, তবে নবম সংখ্যা হবে 36. ”-তম সংখ্যা বার করার সহজ উপায় হলো 1 = a + (n-1) d এই সূত্রটি মনে রাখা ।

”-তম (এখানে নরম) সংখ্যা / ধরলে, 1 = 4+ ( 9 – 1 ) 4, d মানে সাধারণ অন্তর বা Common difference. 28 আর 32-এর মধ্যে কোন সংখ্যা আচে ? একটা শ্ৰেণা যদি a, x, b...এই রকম হয়, তবে x হবে a+b যেমন 28+36-3 2=32.

.

এই ধরনের শ্রেণী, যাতে আগের সংখ্যার সঙ্গে একটা নির্দিষ্ট সংখ্যা যোগ করে-করে পরের সংখ্যাগুলো পাওয়া যায়, তাদের বলে সমান্তর প্রগতি (Arithmetical Progression). আর্যভটের বিখ্যাত বইটির দ্বিতীয় অধ্যায়ে (‘গণিতপদ‘) সমান্তর প্রগতির যোগফল (S) এবং পদের সংখ্যা (n) বার করার সূত্রটি একটু অন্য চেহারায় দেয়া আছে। ফরাসি লেখক রোদে তার থেকে অনুমান করেছেন, দ্বিঘাত সমীকরণ (quadratic equation) – এর সমাধানও আর্যভটের জানা ছিল। ব্রহ্মগুপ্তের “ব্রহ্মস্ফুট সিদ্ধান্ত” ও ভাস্করাচার্যের “লীলাবতী”-তেও এ নিয়ে আলোচনা আছে।চীনের পণ্ডিত চ্যাং কিউ কিনও তাঁর বইতে স্কুরিটা দি, প্রগতির কথা লিখেছেন।

এবার তাহলে ধাঁধাটা দেখা যাক । ডাঃ খল্লট অ্যাভিনিউ-এর বাঁদিকের ফুটপাথের বাড়িগুলোর নম্বর জোড়, ডান দিকেরগুলো বিজোড় । এক পিয়ন চিঠি বিলি করতে বেরিয়েছেন। বাঁ ফুটপাথে পা দেয়া মাত্র পাড়ার ছেলেরা এসে ছেকে ধরলো : আমার বন্ধুর দাদার বিয়ের নেমন্তন্নের চিঠি এসচে? আমার ‘ধাঁধা‘ কোথায়? – এর’ম হাজার প্রশ্ন । পিয়নটি তাদের হাত এড়িয়ে 12 নম্বর বাড়ির সামনে দাঁড়িয়ে দ্যাখেন, তাঁর বাঁহাতের বাড়িগুলোর নম্বর যোগ করলে ডান দিকের দুটো বাড়ির নম্বরের যোগফলের সমান হয়। অর্থাৎ তাঁর বাঁদিকে রয়েছে 2, 4, 6, 8 আর 10 নম্বর বাড়ি, আর ডান দিকে রয়েচে 14 আর 16 নম্বর বাড়ি। 70 নম্বর বাড়ির সামনে পৌঁছে দ্যাখেন, ব্যাপারটা আবার তাই হয়েছে। তবে ডান দিকের বাড়ির সংখ্যা স্বভাবতই বেড়ে চোদ্দো হয়ে গ্যাচে। চিঠি বিলি করতে করতে পিয়নটি অনেক দূর চলে গেলেন । এখন একটা বাড়ির সামনে দাঁড়িয়ে দেখলেন, এবারে বাঁদিকে যতগুলো বাড়ি আচে তাদের নম্বরের যোগফল ডানদিকের সব ক-টা বাড়ির নম্বরের যোগফলের সমান । তাহলে বাঁ ফুটপাথে মোট ক-টা বাড়ি ছিল ?

আর, পিয়নটি যখন বিজোড় নম্বরওলা ফুটপাথে যাবেন তখনই বা কোন্ কোন্ বাড়ির তলায় দাড়িয়ে তিনি ঐ রকম বাঁ হাত-ডান হাতের হিসেব মেলাতে পারবেন?

.

26. দুঃসাহসিক ভ্রমণকাহিনী

পৃথিবীর সবচেয়ে আনাড়ি গাড়োয়ানের সঙ্গে চলেছি। গন্তব্য কাটাছেঁড়া থেকে ফাটাজোড়া। ছইএর ভেতর বসে থেকে বাতের চিকিচ্ছে হয়ে যাচ্ছে। শুধু দুঃখ একটাই, আমার বাত নেই । গলা তুলে বলও গাড়োয়ান সাব, তোমার গরুদুটো কি, আর জোর দমে চলতে জানে না ? গাড়োয়ান বললেন, কেন জানবে না কত্তা তবে আরেকটু আস্তে যাবে এই আর কি। ওরে বাবা, তাহলে আর আজকে পৌঁছতে হবে না।

দূরে একটা গ্রাম দেখে প্রায় পেটের দায়েই জিগেস করলুম, কত্তা, ওই গাঁয়ের নামটা যেন কী ? গাড়োয়ান বললেন, ডাবের ছড়াছড়ি ও গাঁয়ে, নাম কানাখোঁড়া। ঘড়িতে দেখলুম, কাটাছেড়া থেকে পনেরো মিনিট আগে বেরিয়েচি। জিগেস করলুম, কানাখোঁড়া আর কদ্দূর ? গাড়োয়ান বললেন, তা কত্তা যদুর এয়েচেন তাথেকে তিনগুণ দূর হবে । কানাখোড়ায় ডাব – টাব খেয়ে আবার তো চললুম । মোট তেরশ গজ যাবার পর কাতর হয়ে বললুম, ফাটাজোড়া আর কদ্দুর বাবা ! আর তো পারি না ! গাড়োয়ানকে তখন কানাখোড়ায় পেয়েছে।বললেন, আজ্ঞে, কানাখোঁড়া থেকে যদ্দুর এয়েচি তাঁর মাত্তর তিনগুণ দূরে ।কোনো রকমে পৈতৃক প্রাণটুকু বাঁচিয়ে, পঁয়তাল্লিশ মিনিট বাদে কোমরে হাত দিয়ে শেষে ফাটাজোড়ায় এসে নাবলুন। মানে গাড়োয়ানই চ্যাংদোলা করে নাবিয়ে দিলো। কতটা পথ পার হলুম বলো তো ?

27. জন্মদিনের কেক

ছেলের হাতে ছুরিটা তুলে দিয়ে ব্যারন মুনচাউসেন বললেন, পাউল, চারটের বেশি কোপ মারবে না, এটাকে যত বেশি পারো টুকরো করে ফ্যালো ।

পাউলের আজ জন্মদিন। পেল্লায় একখানা গোল কেক রয়েছে। এক ফুঁয়ে পাউল ন-টা মোমবাতিই নিবিয়ে দিয়েছে। তারপরেই ব্যারনের এই অদ্ভুত আবদার ।

ছেলেটা বোকা হলে কি হবে, বুদ্ধি আচে। ছুরিটা দিয়ে ঘ্যাচ ঘ্যাচ করে চারটে কোপ মারলো ! ব্যারন টুকরোগুলো গুনে বললেন, ঠিক আছে। পাউলের মাস্টারমশাই গম্ভীর গলায় বললেন, ছুরিটা রাখো। এবার কেকের দিকে না-তাকিয়ে বলো, পাঁচটা, ছটা, সাতটা কোপে সবচেয়ে বেশি কতগুলো টুকরো পাওয়া সম্ভব ? পাউল এটার কোনো উত্তর দিতে পারলো না । কিন্তু, বুদ্ধিমান পাঠক, তুমি কি বলতে পারে। পাউল কী ভাবে কেকটা কেটেছিল, আর মাস্টারমশায়ের প্রশ্নের উত্তরটাই বা কী হবে ? অর্থাৎ, 12- সংখ্যক কোপে সব চেয়ে বেশি কতগুলো টুকরো পাওয়া যায় ?

.

28. হবুচন্দ্র রাজার গোলটেবিল

হবুচন্দ্র রাজার গোলটেবিল বৈঠকে প্রত্যেক লোকের হাতেই কোনো-না-কোনো প্রস্তাব লেখা কাগজ আছে।হবুচন্দ্র রাজার ডানদিকে আছেন গবুচন্দ্র মন্ত্রী। তাঁর হাতের কাগজের সংখ্যা রাজার তুলনায় একটা কম, যদিও তাঁর ডানদিকে বসা কোতোয়ালের তুলনায় একটা বেশি। তাঁর পরের প্রত্যেকের অবস্থাই অবশ্য তাই : বাঁ হাতের লোকের চেয়ে একটা কম প্রস্তাব. ডান হাতের চেয়ে একটা বেশি।হবুচন্দ্র তাঁর প্রস্তাবগুলোর মধ্যে থেকে একটা গবুচন্দ্রকে দিলেন । গবুচন্দ্র সেটা দেখে নিয়ে পাশের কোতোয়ালকে দিলেন, সেই সঙ্গে নিজের একটা প্রস্তাবও গুঁজে দিলেন। কোতোয়াল আবার ঐ প্রস্তাব দুটো আর নিজের একটা, অর্থাৎ তিনটে প্রস্তাব দিলেন তাঁর ডান দিকে বসা বিদূষককে । যতক্ষণ পর্যন্ত না কারুর হাত খালি হছে , ততক্ষণ এইভাবে কাগজ দেয়া-নেয়া চলতে থাকলো । একজনের হাত খালি হতেই কাগজ চালাচালি বন্ধ তখন হিসেব করে দেখা গেলো, গোলটেবিলে উপস্থিত একজনের হাতের কাগজের সংখ্যা তাঁর পাশের লোকের তুলনায় চারগুণ ।

এখন বলো, মোট ক-টা প্রস্তাব ছিল ? আর, বৈঠকীই বা ক-জন ?

.

29. বিভাজ্যতা

এন্‌ট্রান্সে সত্যেন বোস অংক-য় একশ-র মধ্যে একশ পেলেন না কেন? “পরীক্ষার খাতা জমা দিয়া সত্যেন্দ্রনাথ আসিলেন হিন্দু স্কুলে,বক্সী মহাশয় [ স্কুলের বিজ্ঞান পাগল গণিতশিক্ষক‘ উপেন্দ্রলাল বক্সী ] তার অপেক্ষায় আছেন । প্রশ্নপত্র হাতে রাখিয়া দুজনে মুখে মুখে অঙ্কগুলি কষিয়া যাইতে লাগিলেন। হঠাৎ দেখা গেল একটি অঙ্কে সত্যেন্দ্রনাথ 117কে আর ভাঙেন নাই, অবিভাজ্য ভাবিয়া। বক্সী মহাশয় বলিলেন—ন তেরম্ ? দু-জনেরই মুখ অন্ধকার হইয়া গেল।”

তাহলে বিভাজ্যতা ব্যাপারটা খুবই দরকারি ।

7কে 2 দিয়ে ভাগ করলে পড়ে থাকে পেন্সিল, মানে 1. 6কে 2 দিয়ে ভাগ করলে কোনো ভাগশেষ থাকবে না। অর্থাৎ 6 দিব্যি 2 দিয়ে বিভাজ্য । সংক্ষেপে 2।6.

এখন, কোনো সংখ্যা যে অন্য একটি সংখ্যা দিয়ে বিভাজ্য সেটা এক নজরে বলব কী করে? ভাগ করে ? অদ্ভুত ! ভাগ করে দেখে বলব, ভাগ করা যায় কিনা? ডিমটা ভেঙে তবে বলব পচা না ভালো! তোমার মা-কে অত ঝামেলা করতে হয় না, এক নজরে বুঝে নেন। তেমনি, কোনো সংখ্যা (ধরা যাক 1235813 ) 2, 3, 4, 5, 9 দিয়ে বিভাজ্য কিনা জিগেস করলে সব ক-টা ভাগ

করে বলতে কত সময় লাগবে ? অবশ্য সোমেশ বস্তু বা শকুন্তলা দেবী হলে অন্য কথা ৷

বিভাজ্যতার সমস্যা সমাধানের জন্যে কয়েকটা সহজ নিয়ম আচে, ইংরিজিতে যাকে বলে rule of thumb. যেমন :

1. সব সংখ্যাই, বলাই বাহুল্য, 1 দিয়ে বিভাজ্য ।

2. যদি কোনো সংখ্যার শেষ অংকটা জোড় হয়, তবে সেটি 2 দিয়ে বিভাজ্য। মনে রেখো, শূন্যও জোড় সংখ্যা।

3. যদি কোনো সংখ্যার সংখ্যামূল 3, 6 বা 9 হয়, তবে সেটি 3 দিয়ে বিভাজ্য। যদি কোনো সংখ্যার সংখ্যামূল 5 হয়, তবে সংখ্যাটিকে 3 দিয়ে ভাগ করলে ভাগশেষ হবে 2.

4. কোনো সংখ্যার শেষ দুটো অংক যদি 4-এর নামতার আওতায় পড়ে, তবে সেটি 4 দিয়ে বিভাজ্য।

5. কোন সংখ্যার শেষে 5 বা 0 থাকলে সেটি 5 দিয়ে বিভাজ্য ।

6. কোনো সংখ্যা যদি জোড় হয়, আর তার সংখ্যামূল যদি 3 দিয়ে বিভাজ্য হয়, তবে সেটি 6 দিয়ে বিভাজ্য। বুঝতেই পারছ, 6 মানে 2×3, সুতরাং 2 আর 3-এর বিভাজ্যতার নিয়ম এক সঙ্গে খাটালেই হলো।

7. এটা একটু ঝামেলার । তবে ছ-অংকগুলা সংখ্যার (যেমন, 873378 ) বেলায় সংখ্যাটাকে 873873 থেকে বিয়োগ করো । বিয়োগফল যদি 7 দিয়ে বিভাজ্য হয়, তবে সংখ্যাটাও 7 দিয়ে বিভাজ্য হবে । যদি না হয়, হবে না । ( হঠাৎ 873873 নিলুম কেন বলতে পারো ? )

8. কোনো সংখ্যার শেষ তিনটি অংক যদি ৪-এর নামতার আওতায় আসে, তবে সেটি ৪ দিয়ে বিভাজ্য ।

9. কোনো সংখ্যার সংখ্যামূল যদি 9 দিয়ে বিভাজ্য হয়, তবে সংখ্যাটিও 9 দিয়ে বিভাজ্য ।

10. 10-এর নিয়মটাও কি বলতে হবে ? সংখ্যাটার শেষে ০ থাকলেই দশের দশা ।

7, 11 আর 13-র বেলায় আরো সুন্দর একটা নিয়ম আছে। সংখ্যাটা যদি ছ-অংকের বেশি ( বা কমও ) হয় তাহলেও দিব্যি বিভাজ্যতা বার করা যাবে। ডান দিকের তিনটে করে সংখ্যার একটা দল নিয়ে একবার বিয়োগ আরেকবার যোগ করে চলো। এবার দ্যাখো উত্তরটা 7 বা 11 বা 13 দিয়ে বিভাজ্য কিনা ।

ধরো 78362494. 494 – 362 + 78 = 210, এটি 7 দিয়ে বিভাজ্য (10 দিয়েও), 11 বা 13 দিয়ে নয়। সুতরাং মূল সংখ্যাটাও 7 দিয়ে বিভাজ্য, 11 বা 13 দিয়ে নয়। বিয়োগফল যদি 0 হয়, তাহলে মূল সংখ্যাটা 7, 11, 13  ক তিনটে দিয়েই বিভাজ্য ।

11-র ক্ষেত্রে আরেকটা কৌশল আছে। প্রত্যেকটা অংককে বিয়োগ-যোগ করে চলো : উত্তরটা যেই 11-র নামতার আওতায় পড়লো, সংখ্যাটাও 11 দিয়ে বিভাজ্য। 647152 কে লেখা হবে 6-4+7-1+5-2-11, কাজেই এটা কেন হয় বলতে পারো ? আর বলো তো, 0 আর 1 দিয়ে তৈরি সব চেয়ে ছোটো কোন্ সংখ্যা 72 দিয়ে বিভাজ্য ?

.

30. উড়নচণ্ডীতলা হাউসিং এস্টেট

উড়নচণ্ডীতলায় নতুন হাউসিং এস্টেট নিয়ে সে যে কী ঝামেলা কী ঝঞ্ঝাট কী বলব । খবরের কাগজে চিঠি লেখালেখি, কর্তাদের মুণ্ডুপাত (অবশ্য কথায়), বিধানসভায় লোকসভায় জোর প্রশ্নোত্তর– কিছু বাদ যায় নি। এখনো বোধহয় সুপ্রিম কোর্টে মামলা ঝুলচে।

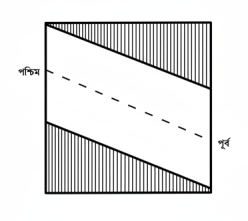
ব্যাপারটা হয়েছিল এই : উড়নচণ্ডীতলায় জমিটা ছিল চতুষ্কোণ, প্রত্যেকটা দিক পৌনে এক মাইল লম্বা। বাড়ি ঘর তৈরি হবে কেবল কালো দাগকাটা দুটো ত্রিকোণ এলাকায় । মধ্যের পুরো এলাকায় থাকবে বারোয়ারি ক্ষেত। আলু পটল উচ্ছে টাঁড়িসের চাষ হবে, আর তার ঠিক মধ্যে দিয়ে পূর্ব থেকে পশ্চিমে চলে যাবে একটা পাকা রাস্তা । ক্ষেতের জন্যে এতটা জমি বরাদ্দ করা নিয়েই অত হল্লা হয়েছিল । ক্ষেতের এলাকাটা সত্যিই নেহাত কম ছিল না, পুরো এস্টেটের এলাকার সাতের বারো ভাগ! মধ্যের রাস্তাটার দৈর্ঘ্য তাহলে কত ছিল?

.

31. বাজার করার হাজার ঠ্যালা

অলাকবাবু সেদিন ওল্ড মার্কেটে গিয়ে কিছু কমলালেবু কিনলেন । একটা দুটো নয়, কমলালেবুর সংখ্যা 1000 থেকে 9999 এর মধ্যে । প্রত্যেকটা লেবুর দাম : কয়েক আনা, কয়েক পাই ( 1 আনা = 12 পাই ) । তারপর তিনি কিছু আপেলও কিনলেন। আপেলের সংখ্যা হলো কমলালেবুর সংখ্যার সহস্রের অংকটা বাদ দিলে যত হয় তত। আবার, একটা আপেলের দাম হলো লেবুর দামের ঠিক উল্টো। অর্থাৎ কমলালেবুর দাম যত আনা, আপেলের দাম তত পাই, ওটার যত পাই, এটার তত আনা । বুঝতে অসুবিধে হচ্চে? আচ্ছা । কমলালেবুর দাম x আনা y পাই হলে, আপেলের দাম y আনা x পাই । কিন্তু কীলে আশ্চর্য! অলীকবাবু অবাক হয়ে দেখলেন, মোট কমলালেবুর দাম আপেলগুলোর দামের সমান। কমলালেবুই বা ক-টা ছিল, আর এক-একটা কমলানেবুর দামই বা কত ছিল ?

.

32. টোপোলজি

ক্যোনিসবার্গ, প্রুশিয়া – প্রেগেল নদীর তীরে, বেঞ্চিতে বসে গালে হাত দিয়ে ভাবছিলেন হের ক্লুগ।

নদীটা বয়ে যাবার পথে দু-ভাগ হয়ে একটা দ্বীপ তৈরি করেছে। পারাপারের জন্যে রয়েচে সাতটা সেতু। হের ক্লুগ ভাবছিলেন:কোনোটার ওপর দিয়ে দুবার না গিয়ে সাতটা সেতুই কি পার হওয়া সম্ভব?

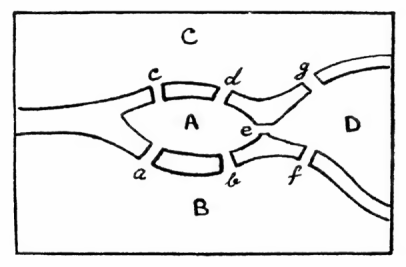
ক্লুগ অনেক ভাবলেন । কোনো সুরাহা হলো না। হঠাৎ মনে পড়লো লেওনহার্ড অয়লার-এর কথা।

অয়লার তাঁর বন্ধু, বাঘা অংকবিদ। দ্যাখা যাক এ ব্যাপারটায় কিছু করতে পারে কিনা। সমস্তটা শুনে এক টিপ নস্যি নিয়ে অয়লার বললেন, হু । তারপর খসখস করে নদীর পথ, দ্বীপ ও সেতুগুলোর নকশা এঁকে ফেললেন । নিজের মনেই তিনি বললেন, ধরা যাক, নদী দিয়ে ভাগ করা চারটে স্থলভূমি হলো A,B,C,D ; আর সেতুগুলোর নাম a, b, c, d, e, f g A থেকে B তে a অথবা b সেতু দিয়ে যাওয়া যাবে । এই যাওয়ার পথের নাম দেয়া যাক AB B থেকে D-তে যেতে হলে f সেতু, তার নাম তাহলে BD. আর এই পথে A থেকে B, B থেকে D-তে যাওয়ার পথের নাম হবে ABD. সেখান থেকে আবার C-তে গেলে ABCD, কেমন তো? ক্লুগ আগেই ভেবেছিলেন যে এই পথে যেতে হলে তিনটে সেতু পার হতেই হবে, আর তা লিখতে চারটে অক্ষর লাগবে। সুতরাং সাতটা সেতু একবার ঘুরে এলে পথটা লিখতে হবে আটটা অক্ষরে । তিনি চুপচাপ ঘাড়

নাড়লেন ।

অয়লার বলে চললেন, কিন্তু যাওয়া-আসার সেতুর দিকে একদম নজর দেয়া হয় নি। A ও B-র মধ্যে দুটো সেতু আছে, সুতরাং AB ( বা BA ), AC ( বা CA ) — দুবার, BD আর DC একবার থাকবে। হঠাৎ তাঁর কী খেয়াল হলো, বললেন, আচ্ছা, ধরা যাক A এমন একটা জায়গা যেখান থেকে বেরোবার অনেক সেতু, যেমন a, b, c, d ইত্যাদি, আচে । শুধু a পার হলে বুঝতে হবে হয় আমি A-তে ছিলুম, নয় a পার হয়ে সদ্য A-তে এসে পৌঁছেচি । সুতরাং

.

a পার হলে শুধু A লেখাই যথেষ্ট। যদি A-তে আসা-যাওয়ার তিনটে সেতু থাকে এবং আমি তিনটেই পার হই তবে যাওয়ার পথ দ্যাখাতে হলে দুবার A লিখতে হয়, সে A থেকেই শুরু করি আর A-তে এসেই পৌঁছই । A থেকে যাওয়া-আসার জন্যে পাঁচটা সেতু থাকলে তিনবার A লিখতে হবে। তাহলে, একগাল হেসে অয়লার বললেন, সেতুর সংখ্যা যদি বিজোড় হয়, তবে তার সঙ্গে এক যোগ করে দুই দিয়ে ভাগ করলে যাওয়ার পথে A কবার লিখতে হবে জানা যাবে। আর আমাদের প্রেগেল নদীর ব্যাপারটা দাঁড়ালো এইঃ A-র সঙ্গে পাঁচটা সেতুর যোগাযোগ, সুতরাং A লিখতে হবে তিনবার। সেরকম B, C, D থাকবে দুবার । তা’লেই বুঝলে, সাতটা সেতু একবার করে পার হতে ন-টা অক্ষর লাগচে । সুতরাং বৃথা চেষ্টা, এক ঢিলে সাতটা পাখি মারা যায় না ক্লুগ আপত্তি করতে যাচ্ছিলেন।হাত নেড়ে তাকে থামিয়ে অয়লার বললেন, দেখো, যদি A থেকে শুরু না করো তবে A একবারই লিখতে হবে । কিন্তু A থেকে শুরু করলে দুবার। আর সেতুর সংখ্যা জোড় হলে A লিখতে হতো সেতুর সংখ্যার আদ্ধেকবার, বিজোড় হলে তার সঙ্গে এক যোগ করে তার অর্ধেক।

এই ব্যাঁকাচোরা পথে যাতায়াতের সমস্যা নিয়েই টোপোলজির জন্ম। টোপোলজি মানে ব্যাঁকাচোরার জ্যামিতি ! এখন এই দুটো সমস্যা দেখো :

.

.

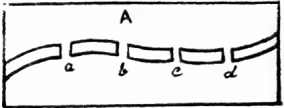
আর্যাবর্ত আর দাক্ষিণাত্যের কয়েকটা শহর আর তাদের মধ্যেকার রেলপথের ছবি দেয়া আছে। প্রত্যেক পথে একবার মাত্র গিয়ে সব ক-টা শহর ঘুরে আসতে পারবে ? যে-কোনো শহর থেকে শুরু করে যে-কোনো শহরে এসে থামতে পারো

.

33. পৃথিবীর সূত্রবলয়

বিশ্বামিত্র একবার রেগে গিয়ে ব্রহ্মার সঙ্গে পাল্লা দিয়ে নতুন জগৎ তৈরি করতে নাবলেন। প্রথমেই তাঁর লক্ষ্য হলো একটা ‘আগাপাসতলা নতুন পৃথিবী তৈরি করা। বিরাট লম্বা এক দড়ি নিয়ে লাগলেন মাপজোক করতে। বিষুবরেখা বরাবর দড়িটা পেঁচিয়ে যখন দুটো মুখ এক করতে গ্যাছেন – দ্যাখেন মহা মুশকিল । পুরোটা বেড় দিয়ে দড়িটার একটা মুখ একগজ বাড়তি রয়ে গ্যাছে ।দড়ির দুটো মুখ এক করে তখন তিনি বিষুবরেখার সঙ্গে সমান্তরাল এক সূত্রবলয় তৈরি করলেন দূর থেকে দেখলে মনে হবে যেন দ্বিতীয় শনি গ্রহ ।

পাশে দাঁড়িয়ে সমস্ত ব্যাপারটা দেখছিল ময়দানব। বিশ্বামিত্র এক ধমক মেরে বললেন, ফ্যাচফ্যাচ করে হাসছিস্ যে বড়ো ? বলতো, পৃথিবী থেকে আমার এই সূত্র বলয়ের ব্যবধান কত? ময়দানব শুক্রাচার্যের কাছে অংক শিখেছিল। উত্তর দিতে তার সময় লাগলো মাত্তর তিন অনুপল ।

তোমাদেরো তার বেশি সময় লাগার কারণ নেই।

.

34. নোন্তার বুদ্ধি

আমাদের পাড়ার শ্রীমান্ নোন্তা সবে সাত পুরে আটে পড়েছে, কিন্তু বুদ্ধিতে ব্যাটা বৃহস্পতি। সেদিন ইস্কুল থেকে ফিরে মাঠে গ্যাছে ঢেঁকুচকুচ চড়তে। কিন্তু মাঠে একটা ছেলে নেই যাকে অন্যদিকে বসাবে। ঢেঁকুচকুচটার একটা দিক আবার গেছে ভেঙে। কিন্তু দমে যাবার ছেলে নোন্তা নয়। এদিক-ওদিক তাকিয়ে দ্যাখে, মাঠের ধারেই একটা নতুন বাড়ি তৈরি হচ্চে। এক পাজা ইট রয়েছে। দেখে শুনে নোন্তা আঠারোটা ইট নিয়ে এলো। যখন সেগুলোকে ঢেঁকুচকুচের ভাঙা দিকটায় রাখে তখন ব্যালেন্স করার জন্যে সব ক-টাই দরকার ৷ লম্বা দিকটাতে অবশ্য আটটা রাখাই যথেষ্ট। একটা ইটের ওজন যদি পৌনে একটা ইট আর পৌনে এক কে.জি-র আদ্ধেকের সমান হয় তবে নোন্তার

ওজন কত?

.

35. হ য ব র ল-র বিচারসভা

আসামী ন্যাড়ার পিঠে মোটা বইটা দিয়ে থাবড়া মারতে মারতে শেয়াল বললো, দাঁড়াও, জেরার চোটে সব ফাঁস করে দিচ্ছি। বলে কনস্টেবল খরগোশকে বললে, তুমি বলছ যখন তুমি ছুটতে আরম্ভ করলে আসামী তখন তোমার থেকে সাতাশ পা দূরে ছিল?

— হ্যাঁ।

–এবং তুমি শপথ করে বলতে রাজি আছ যে তুমি পাঁচ পা গেলে সে আট পা যায়?

–ঠিক তাই ।

—তাহলে তুমি তাকে ধরলে কী করে? এয়ার্কির জায়গা পাওনি!

—দেখুন, ব্যাপারটা বুঝছেন না। আমার লাফগুলো ওর থেকে লম্বা । আমার দু পা যাওয়া মানে আসামীর ছোটায় পাঁচ পা । এখন একটু খেয়াল করলেই বুঝবেন, ক-পা গেলে ঠিক যে জায়গায় আসামীকে পাকড়েচি সেখানে পৌঁছনো যায় ।

হাকিম প্যাঁচা চোখটা খুলে একটু হিসেব করে নিয়ে বললো, ঠিক আছে। আসামীর তিনমাস জেল আর সাতদিন ফাঁসির হুকুম হলো।

খরগোশ কি সত্যিকথা বলেছিল?

.

36. স্বল্পতম দূরত্ব

সরলরেখায় বয়ে চলেচে বিশীর্ণা নদী । তীর থেকে 3 গজ দূরে A বিন্দুতে বসেছিলেন ভাস্করাচার্য (জুনিয়র) । হঠাৎ নজরে পড়লো তীর থেকে 6 গজ দূরে B বিন্দুতে একটা বাড়িতে আগুন লেগেছে । A থেকে B-র দূরত্ব সোজাসুজি 5 গজ। ভাগ্য ভালো, হাতের কাছেই বালতি ছিল। সোজা ছুটলেন নদী থেকে জল নিয়ে। অংকটা জানতেন বলে রক্ষে, স্বল্পতম দূরত্বটুকু মনে-মনে কষে তাড়াতাড়ি পৌঁছে জল ঢালতে লেগে গেলেন ।

ভাস্করাচার্য (জুনিয়র) কতটা ছুটেছিলেন?

.

37. পাঁচে বহুতল ছয়ে গ্রহ

খ্রীষ্টপূর্ব পঞ্চম শতাব্দীর গ্রীক দার্শনিক প্লাতোন ( ইংরেজরা যাকে প্লেটো বলে) ভেবেছিলেন, ঈশ্বর হলেন পয়লা নম্বরের জ্যামিতিবিদ। ফলে তাঁর সৃষ্টির পথে ছড়ানো রয়েচে শুধু সুষমা আর সামঞ্জস্য। কোপার্নিকাস, গালিলিও আর নিউটন এর মধ্যে যিনি সাক্ষাৎ হাওড়া ব্রিজ, সেই ইওহানেস কেপলার ( 1571-1630 ) এ-ব্যাপারটা এতই বিশ্বাস করতেন যে প্লাতোন-এর “তিমায়েউস”-এ যে পাঁচটি সুষম বহুতলের ( regular polyhedra ) কথা আছে, তাদের সঙ্গে সৌর মণ্ডলের ছ-টি গ্রহের ( ইউরেনস, নেপচুন আর প্লুতোর তখনো অবধি হদিশ মেলে নি ) আয়তনের তিনি একটা সম্পর্ক খুঁজে বার করলেন। শনির গোলকটা যদি একটা লুডোর ছক্কার চারধারে পরিলিখিত (circumscribed) হয়, যার ভেতরে রয়েছে বৃহস্পতির গোলক, আর বৃহস্পতির গোলকের ঠিক ভেতরে যদি একটা পিরামিড থাকে, যার মধ্যে অন্তর্লিখিত ( inscribed) রয়েছে মঙ্গলের গোলক, এবং এইভাবে আর তিনটি বহুতলের ভেতরে ও বাইরে আর তিনটি গ্রহের গোলক থাকে, তবে গ্রহগুলির আয়তন সম্পর্কে কোপার্নিকাস-এর হিসেব ঠিক বলে প্রমাণ করা যাবে । এই জন্যেই গ্রহের সংখ্যা ছয়, আর সেগুলো পরের পর ঐ ভাবে সাজানো আছে। “ব্রহ্মাণ্ডের রহস্য”তে একথা বলার কুড়ি বছর বাদে, “জগতের সামঞ্জস্য” বইটিতে তাঁর বিখ্যাত তৃতীয় সূত্রটি বলার সময়েও কেপলার একটু ঘুরিয়ে এই বিচিত্র প্রমাণ (?)-টি দিয়েছিলেন। বুঝতেই পারছ, কত গভীর ছিল সুষম বহুতলের টান :

সুষম বহুতল জিনিসটা কী? লুডোর ছক্কাটার কথাই ভাবো। এর প্রত্যেকটা পিঠই একটা করে বর্গক্ষেত্র, ছ-টি পিঠে বর্গক্ষেত্র রয়েছে, যার অন্তঃকোণগুলি সমান । সুষম বহুতল তাকেই বলা হবে যার প্রত্যেকটি পিঠে সমান সংখ্যক বাহু ও শীর্ষ রয়েছে। অন্য কথায়, সমান দৈর্ঘ্য ও প্রস্থের সরল রেখা দিয়ে দু-মাত্রায় যেমন সুষম বহুভুজ আঁকা যায়, তেমনি তিনমাত্রায় সুষম বহুতলও তৈরি করা যায় ।

এখন মজাটা হলো, সুষম বহুভুজের সংখ্যার কোনো সীমা-পরিসীমা নেই। সমবাহু ত্রিভুজ, বর্গক্ষেত্র, সুষম পঞ্চভুজ, অষ্টভুজ, বিংশভুজ, সহস্রভুজ আঁকা সম্ভব। কিন্তু সুষম বহুতল বা সমঘন (regular solids)-এর সংখ্যা বড়োই কম। কেপলার-এর আমল পর্যন্ত লোকে পাঁচটার কথা জানতো। সেগুলো হলো:

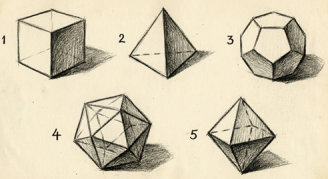
1. ষট তল (Hexahedron বা cube)

2. চতুস্তল (Tetrahedron বা pyramid)

3. দ্বাদশতল (Dodecahedron)

4. বিংশতল (Icosahedron)

5. অষ্টতল (Octahedron)

ফরাসি দার্শনিক-অংকবিদ দেকার্ত এদের শীর্ষ (vertex), ধার (edge) ও পিঠ (face) গুলির মধ্যে একটা সম্পর্ক প্রথম লক্ষ করেন, পরে লেওনহার্ড, অয়লার তার প্রমাণটাও দ্যান। ব্যাপারটা হলো এই যে, পাঁচটা বহুতলের শীর্ষ ও পিঠের সংখ্যা ধারের সংখ্যার চেয়ে দুই বেশি। অর্থাৎ V + F = E + 2. নিচের হিসেবটা দ্যাখো:

.

নাম	শীর্ষের সংখ্যা (V)	ধারের সংখ্যা (E)	পিঠের সংখ্যা (F)	V+F	E+2
চতুস্তল	4	6	4	8	8
ষটতল	8	12	6	14	14
অষ্টতল	6	12	8	14	14
বিংশতল	12	30	20	32	32
দ্বাদশতল	20	30	12	32	32

.

এই ফাঁকে একটা কথা বলে নি । এই পাঁচটা সুষম বহুতলের সঙ্গে কেপলার আরো দুটো যোগ করেছিলেন : তারার মতো দেখতে দুটি দ্বাদশতম ( ছোটোটির F = 12, V = 12, E= 30, বড়োটির F = 12, V = 20, E= 30 ) । পরে পোআঁসো ( 1777-1859 ) আরো দুটো সুষম বহুতলের কথা বললেন : বৃহৎ বিংশতল ( F = 20, V = 12, E = 30 ) আর বৃহৎ দ্বাদশতল ( F = 12, V = 12, E = 30 )। এই নতুন চারটের মধ্যে দুটি অয়লার-এর উপপাদ্যের সঙ্গে মেলে, দুটি মেলে না। ক্যাণ্ডি ও রলেট-এর “ম্যাথামেটিক্যাল মডেল্স্ ” ( অক্সফোর্ড, 1964 ) বইটিতে এই সব কটার ছবিই দেখতে পাবে ।

সুষম বহুতলের সংখ্যা তাহলে দাঁড়ানো 9, আর আমাদের সৌরজগতের ন-টা গ্রহ ঘুরে চলেছে। গ্রহগুলির আয়তন সম্পর্কে কেপলার যে-হিসেবটা করেছিলেন, সেটার মধ্যে কুসংস্কারের ছাপ ছিল ঠিকই। কিন্তু শেষ পর্যন্ত সংখ্যার সামঞ্জস্যটা রয়েই গেলো, আর কেপলারই তার গোড়াপত্তন করে গেলেন!

এত জ্ঞানের কথা কেন বললুম ? সহজ কথা, কাগজ দিয়ে সুষম বহুতল তৈরি করব বলে । সহজ জিনিস দিয়েই শুরু করা যাক । একটা চতুস্তল বা পিরামিড খাড়া করা যাক ।

একটা খাম জোগাড় করো। তার দুপিঠেই দুটো সমবাহু ত্রিভুজ এঁকে নাও। তারপর ছবিতে যেমন দ্যাখানো আছে তেমনি ভাবে স্ট্যাম্প-মারা অংশটুকু ছিড়ে নাও। ব্যস, এবার দুটো কোণ (A আর B) বাহু বরাবর এক করো, সুন্দর পিরামিড পেয়ে যাবে । ছেঁড়া দিকটা আঠা বা পিন বা সেলোটেপ দিয়ে আটকে দাও।

.

.

আরেকটা ব্যাপার একটু চেষ্টা করে দ্যাখো। একটা চতুষ্কোণ ( বর্গক্ষেত্র ) কাগজ নাও, তাতে দুটো ভাঁজ দিয়ে একবার কেটে তার থেকে একটা চতুস্তল বানাও তো।

.

লুড়োর ছক্কা হিসাবে ষটতলের ব্যবহার হয়ে থাকে (অবশ্য পাঁচটি সুষম বহুতলই কোনো-না-কোনো খেলায় লাগানো হয়েছে)। এখন একটা 1 ইঞ্চি চওড়া যত ইচ্ছে লম্বা কাগজ ভাঁজ করে যদি ছক্কা বানাতে হয় তবে কাগজটাকে কমপক্ষে ক-টা বর্গক্ষেত্রে ভাগ করবে? এটা ঠিক করতে পারলে ছক্কা তৈরি করতে আর কোনো ঝামেলা হবে না।

.

38. কাটাকুটি

বাঙালীর ছেলেকে কাটাকুটি খেলা শেখাতে হয় না। বলা যায়, জন্ম থেকেই খেলাটা তার জানা। একটা বয়েস পর্যন্ত, ধরা থাক বারো বছর, সব ছেলেই এ খেলাটা অগাধ উৎসাহে খেলে চলে। তারপর আস্তে আস্তে মজা চলে যায় । একটু ঠাণ্ডা মাথায় খেললে আর হারজিৎ থাকে না, শুধুই ড্র হয়।

কাটাকুটিকে ইংরিজিতে বলে Ticktacktoe. তবে এ খেলা অনেক দিনের পুরনো। যিশুখ্রীস্টের জন্মের অনেক শ বছর আগে থেকেই চীন, গ্রীস, রোমে এ-খেলা চালু ছিল, যদিও তার কায়দা ছিল আলাদা। প্রত্যেক খেলোয়াড় তিনটে করে ঘুটি নিয়ে বসতো। এক-একবার এক-একজন এক-এক ঘরে একটা করে ঘুঁটি বা পয়সা বসাবে। যেই কেউ এক লাইনে লম্বালম্বি, আড়াআড়ি বা কোণাকুণি তার ঘুঁটি বসাতে পারবে, তার জিৎ। যদি কেউই তা না-করতেপারে,

1	2	2
1	.	.
2	1	.

  1 প্রথম খেলোয়াড়ের খুঁটি, 2 দ্বিতীয় খেলোয়াড়ের

তাতেও কিছু এসে যায় না। খেলাটা চলতেই থাকবে, গায়ে লাগাফাঁকা ঘরে খুঁটি সরিয়ে এক লাইনে আনার চেষ্টা করতে হবে। তবে কোণাকুণি খুঁটি সরানো চলবে না, শুধু পাশাপাশি ঘরে খুঁটি সরানো যাবে ৷ মজা করার জন্যে উল্টো-কাটাকুটি বা অ্যান্টিটিকট্যাকটো-ও খেলতে পারে।। যেই কারুর তিনটে খুঁটি এক লাইনে চলে আসবে তার হার ।

কবি ওআর্ডওঅর্থ বাচ্চা বয়েসে বিস্তর কাটাকুটি খেলেছিলেন, বড়ো হয়ে সে-কথা স্বীকার করলেও লজ্জায় আর খেলাটির নাম বলেন নি– -too humble to be named in verse (The Prelude, Book I, পংক্তি 507-13) । কিন্তু ভাবো তো, এত সহজ একটা খেলা, যাতে কোথাও ভাগ্য ভালো বা খারাপ হওয়ার কোনো ‘চানস‘ নেই, দুপক্ষ একটু চোখ খুলে খেললে ড্র যেখানে বাঁধা, সেই খেলাটা এত হাজার বছর ধরে এত জনপ্রিয় রইল কী করে! এ-খেলায় জেতার একমাত্র গ্যারান্টি হলে। দুর্বল অর্থাৎ চূড়ান্ত অন্যমনস্ক এবং / অথবা ভীষণ বোকা এবং / অথবা একেবারেই অবোধ শিশুকে প্রতিপক্ষ বেছে নিয়ে তাকে দো-ফাঁদে ফ্যালা । মধ্যের ঘরটা প্রথম চালেই আটকে রাখলে সেটা করাও খুব সোজা। যে প্রথম চালবে, তার চাল থাকে পাঁচটা। সুতরাং জেতার সম্ভাবনাও তারই বেশি ।

খেলাটা যে এত জনপ্রিয় তার একটা কারণ হলো প্রথম পাঁচটা চাল আলাদা-আলাদা ভাবে মোট 15120 রকম ভাবে দেয়া সম্ভব (কেন বলো তো?) । সুতরাং যতই চাল বদলাও, ‘এবার আরেক রকমে খেলি‘ বলার সুযোগ থাকবেই। সাধারণত যে হেরে যায়, সে-ই উত্তেজিত হয়ে আরেক কায়দায় খেলতে যায়। এবং প্রায়ই আবার হারে।

কাগজে বা শ্লেটে (দু মাত্রায় ) তিন ঘরের কাটাকুটি খেলতে এখন হয়তো আর সকলের ভালো লাগবে না । কিন্তু চার ঘর বা পাঁচ ঘরের কাটাকুটিটা জমবে ভালো। অন্তত মনোযোগের পরীক্ষাটা ভালোই হবে । তিন ঘরের খেলাও একটু নতুন করে খেলতে পারো। তুমি ও তোমার প্রতিপক্ষ যখন ইচ্ছে কাটা ( x ) বা গোল্লা (0) দিতে পারো। তুমি যে-সারিতে কাটা দিলে, সে-ও সেই সারিতেও কাটা দিলো। তুমি এবার তৃতীয় সারিতে কাটা দাও, তোমার জিৎ। আর সে যদি দ্বিতীয় ঘরে গোল্লা দেয়, তখন কী করবে ? অর্থাৎ প্রশ্ন হলো, কার জেতার সম্ভাবনা বেশি, যে প্রথম দাগ মারবে, না যে তার পরে মারবে ?

শেষ কথা : দু মাত্রায় তিন ঘরের কাটাকুটিতে জেতার সম্ভাবনা থাকে মোট আটটা সারিতে ( লম্বালম্বি, আড়াআড়ি, কোণাকুণি ) । চার ঘর বা পাঁচ ঘরের খেলায় মোট ক-টা সারিতে জেতা যাবে? মাত্রা এবং ঘর—দু-এর সংখ্যাই যদি আরো বাড়ানো হয়, তবে তার ক্ষেত্রে সাধারণ সূত্রটা কী হবে?

39. বাসাবদল

একটা 2 8′′×3′ 8″ কাঠ বা পিচবোর্ডের টুকরো জোগাড় করা খুব শক্ত নয়। 1 ইঞ্চি বর্গ আকারের পাঁচটা পিচবোর্ডের টুকরো বসিয়ে নাও (ছবিতে যে-র’ম আচে)। 1 আর 3-এর মধ্যে কিছু নেই। এখন বুদ্ধি করে মোট সতেরো চালে 3 নম্বরের ঘুটিটাকে 6 নম্বরে আর 6 নম্বরেরটাকে 3 নম্বরে পাঠিয়ে দাও। কাজের সুবিধের জন্যে 3 নম্বরটা কালো আর 6 নম্বরটা লাল রং করে নিতে পারো।

.

1	ফাঁকা	3
4	5	6

.

.

40. একটি খুচরো সমস্যা

ছবিতে পাঁচটা মুদ্রা সাজানো আছে—-তিনটে পঁচিশ পয়সার, দুটো দু পয়সার । এখন, একসঙ্গে দুটো করে গায়ে লাগা পয়সা ( একটা পঁচিশ আরেকটা দুই ) সরিয়ে আবার অন্য একটা পয়সার গায়ে লাগিয়ে বসাতে হবে। মধ্যে যে ফাঁক হবে, পাশের পয়সাটা ঠেলে সরিয়ে সেটা ম্যানেজ করা যাবে না। আবার জোড়ে একটা পঁচিশ আরেকটা দুই সেখানে এনে বসাতে হবে। কোনো পয়সা ঘুরিয়ে উল্টো করা চলবে না। এতগুলো না-র বেড়া পার হয়ে কমপক্ষে কত চালে ( সরানো– বসানো মিলিয়ে এক চাল ) পয়সা– গুলোকে এমন করে সাজাতে পারো, যাতে একদিকে তিনটে পঁচিশ আর অন্যদিকে দুটো দুই পাশাপাশি থাকবে ?

আর মুদ্রার সংখ্যা যদি দুই করে বাড়িয়ে চলা হয় ( চারটে পঁচিশ তিনটে দুই, পাঁচটা পঁচিশ চারটে দুই ইত্যাদি ইত্যাদি ) তাহলেই বা ঐ কায়দায় দু ধরনের পয়সা দুদিকে বসাতে কমপক্ষে ক-টা চাল লাগবে ? এর কোনো সাধারণ সুত্র বার করতে পারে?

.

41. ঘড়ি ভাগ

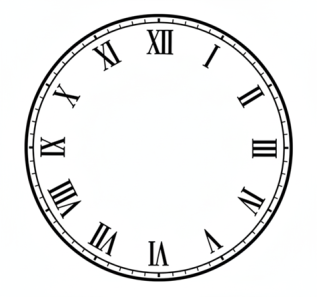
নিচে একটা ঘড়ির ডায়ালের ছবি রয়েচে। I থেকে XII অবধি লেখা এই বৃত্তটাকে এমন চার ভাগে ভাগ করো যাতে প্রত্যেক ভাগের সংখ্যাগুলোর যোগফল 20 হয় ।

.

.

42. দ্যাখার ভুল

পরশু রাতে পষ্ট চোখে দেখনু বিনা চশমাতে

পান্তভূতের জ্যান্ত ছানা করছে খেলা জোছনাতে।

বলেছিলেন ‘আবোল-তাবোলে’র কবি। অবশ্যই এতে আপত্তির কোনো কারণ থাকতে পারে না । দেখতে চাইলে কত কী দ্যাখা যায়। তোমার দু হাতের বকবার আঙুল দুটো ( সংস্কৃত-য় যাকে বলে তর্জনী ) এক করে, বাকি আঙুলগুলো মুড়ে, চোখের লেভেল-এ তুলে, সামনের কোনো সাদা দেয়ালের দিকে তাকিয়ে থাকো (খবরদার! আঙুলগুলোর দিকে নয় ! ) । খানিক বাদে আঙুল দুটো একটু ফাঁক করো, পষ্ট দেখবে আরেকটা আঙুল, একটু ছোটো মতো দেখতে, দিব্যি পুলিপিঠের মতো চোখের সামনে শূন্যে ভাসচে। এবার ভালো করে আঙুল দুটোর দিকে তাকাও। ব্যস, পিঠে নিরুদ্দেশ।

একটা কাচের গেলাস, মানে যাতে আমরা জল-টল খাই আব

কি, কতটা লম্বা ? হাতের তেলোটা সোজা করে বলো তো, মধ্যমার ডগা থেকে কতখানি হবে ? কব্জি পর্যন্ত ? এবার মেপে দ্যাখো, সব ক–টা কররেখাও পার হয় নি। দ্যাখো দিকি, তোমার নিজের চোখদুটো তোমার সঙ্গেই কী র’ম বিশ্বাসঘাতকতা করচে।

এখন এই লাইনদুটোর দিকে তাকাও। কোনটা বেশি লম্বা?

তলারটা তো? আবার তোমার চোখ বিশ্বাসঘাতকতা করেছে । দুটো লাইনই সমান । আসলে চোখদুটোকে দোষ দিয়েও খুব লাভ নেই। যখনই আমরা কোনো কিছু দেখি, তখন তো আর সবাই অর্জুন হয়ে যাই না। পাখির চোখ ছাড়াও চারধারের আরো অনেক কিছু দেখি। দ্রোণাচার্য বৃথাই কুরুপাণ্ডবদের ধমকেছিলেন । এক চোখ না–বুজে লক্ষ্যস্থির করাও বড়ো সহজ কাজ নয়। ঐ লাইন দুটোর ব্যাপারে তোমার ভুলটা হয়েচে পাশের <>আর >< চিহ্ন গুলোর জন্যে ।

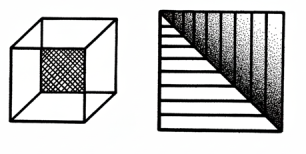
তারপর ধরো মাথার মধ্যে এমন সব ছবি আগে থাকতে তৈরি হয়ে থাকে যে, অনেক সময় অদ্ভুত অদ্ভুত কথা বলে ফেলি। 55″ একটা ছেলেকে দেখলে বলবে, মাঝারি গোছের লম্বা। আর ঐ একই 55” লম্বা একটা মেয়েকে দেখে বলবে, বাব্বা, কী ঢ্যাঙা ! এবার তলার ছবি দুটো দ্যাখো। ছবিটা দেখতে–দেখতে চড়াক করে কেমন যেন ঘুরে যায় !

.

.

.

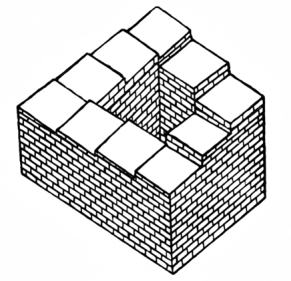
এবারে এই অদ্ভুত পাঁচিলটা। এর যে-কোনো একটা ধাপ থেকে উঠতে শুরু করো, উঠতে উঠতে আবার সেই ধাপেই এসে থামবে। আবার ঐ ধাপ থেকেই নীচে নাবতে থাকো, সেই ধাপেই নেবে থামবে ! আরো পরখ করে দেখতে চাও দ্যাখো – হয় উঠেই চলেচে, নয় নেবেই চলেচে। ব্যাপারটাই ঐ রকম !

.

43. রাজার খেলা দাবা

আউটডোর খেলার রাজা হলো ক্রিকেট, ইনডোরের দাবা । চৌষট্টিটা সাদা-কালো ঘর, সাদা-কালো রাজা, মন্ত্রী, গজ, ঘোড়া, নৌকা, বোড়ে—এই নিয়ে রাজায় রাজায় লড়াই । প্রত্যেকের চাল আলাদা আলাদা । বোড়ে যায় প্রথমে দু পা (ইচ্ছে করলে এক পা), তারপর মাত্র এক পা, শুধু খাওয়ার সময় কোণাকুণি । নৌকো আটটা ঘরেই সোজাসুজি চলতে পারে। গজ ছোটে কোণাকুণি । মন্ত্রী একই সঙ্গে নৌকো ও গজ—দু-এর মতোই চলতে পারে। রাজা বেচারা এক ঘরের বেশি চলতে পারে না। এ-খেলা যে জানে তার জন্যে অবশ্য এ-সব বলা বাহুল্য । যে জানে না তারও কোনো সমস্যা নেই, ছবিটা দেখলেই বুঝতে পারবে মন্ত্রীর চলাচল কোন পথে ।

.

.

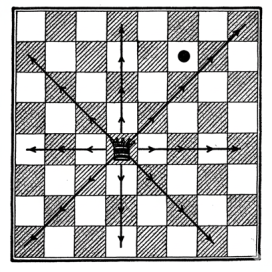
এখন মন্ত্রীকে মন্ত্রণা দিতে হবে কী করে তিনি ওপর থেকে দু– নম্বর সারির ডান দিকের তিন নম্বর ঘর থেকে ( দাবা খেলায় যার নাম K B 7 বা f 7 ) যাত্রা শুরু করে সোজা পথে ( অর্থাৎ নৌকোর মতো) মাত্র পনেরোটা চালে বোর্ডের সব ক-টা ঘর ঘুরে আসতে পারেন। অবশ্যই মন্ত্রীমশাই কোনো ঘরে দুবার যাবেন না, তবে যে-কোনো ঘরে এসে থামতে পারেন ।

দ্বিতীয় কথা, আটটা সারিতে মন্ত্রী এমন ভাবে বসাতে পারো যে, কেউ কাউকে খেতে পারবে না ?

.

44. টোপোলজির খেলা

তিন ফালি কাগজ নিয়ে দুটো মুখ আঠা দিয়ে জুড়ে নাও। তারপর ছবিতে যেমন দ্যাখানো হয়েছে তেমনি প্রথমটাকে সোজা রেখে, যে কোনো একটা মুখ ধরে দ্বিতীয়টাকে 180° আর তৃতীয়টাকে 360° পাক খাওয়াও। এবার ভেতরের দাগ বরাবর কাঁচি দিয়ে কেটে

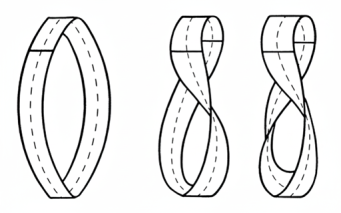
চললে প্রথমটা থেকে দুটো আলাদা ফালি বেরিয়ে আসবে। দ্বিতীয় আর তৃতীয়টার চেহারা কী র’ম দাড়াবে? দুটো আলাদা ফালি পাবো, নাকি অন্য কিছু হবে? আগে ভাবার চেষ্টা করো, তারপর কাটো।

45. তাসের দেশ

একটা প্যাকেটে ক-টা তাস থাকে? বাহান্নটা । এক বছরে ক-টা হপ্তা? বাহান্ন। টেক্কাকে ইংরিজিতে বলে ACE, এই Ace থেকে Two, Three,…King পর্যন্ত তাসগুলোর নাম লিখে সব ক-টা অক্ষর যোগ করো, যোগফল বাহান্ন । সব ক-টা তাসে যতগুলো ফোটা আচে, যোগ করো (গোলামকে 11, বিবিকে 12 আর সায়েবকে 13 ধরে) – যোগফল 364, একটা জোকার আছে, তাহলে + 1, মানে 365, অতিবর্ষ বা লিপ ইআর-এর জন্যে আরেকটা জোকার তোলা রইল।

3+6+5=14, দিব্যি 7 দিয়ে বিভাজ্য ।

7 কেন ? 52-র 5+2= 7, ব্যাপারটা কী র’ম হলো?

এখন নিচে যে ষোলোটা তাস সাজানো আছে, সেইভাবে তুমিও সাজাও। তারপর বন্ধু-বান্ধবদের বলো, যার য-টা ইচ্ছে তাস উল্টে রাখুক। তুমি তখন পাশের ঘরে বসে রেডিও শুনতে পারো । আরো মজা দ্যাখাতে চাও তো কাউকে বলো একটা ইয়া মোটা কাপড় দিয়ে তোমার চোখ বেঁধে দিতে। সকলের তাস ওলটানো শেষ হলে ঘরে ঢুকে বা চোখের বাঁধন খুলে একবার তাকাও—তার– পর পটাপট বলে দাও কোন্ কোন্ তাস ওল্টানো হয়েছে ।

কী করে বলবে? দ্যাখো, প্রত্যেকটা তাসের মাঝের ফোটাগুলো ওপর দিকে মুখ করে রয়েচে। উলটে দিলে চেহারা তো পাল্টাবেই। তাহলে আর বুঝতে অসুবিধে কী!

সব তাসে কিন্তু এ-খেলা দ্যাখানো যাবে না । ওপরের ষোলোটা তাস ছাড়া আর মাত্র ছ-টা তাসের এ গুণ আচে। সেগুলো কী কী ?

.

46. ব্রহ্মগুপ্তের সমস্যা

তিন সারিতে যে ন-টা বিন্দু রয়েচে তার সব ক-টাকে চারটে সরল রেখা দিয়ে জুড়তে পারবে ? মনে রেখো, কাগজ থেকে পেন্সিল তোলা যাবে না । এটা ওরিগামি নয়, সুতরাং এ-পার ও-ধার ভাঁজ করার কৌশল করতে যেও না যেন!

. . .

. . .

. . .

                        

47. ঘরে-বাইরে

দুটো কাচের গেলাস (পলিথিনেরও নিতে পারো) নিয়ে একটাকে আরেকটার মধ্যে ঢুকিয়ে দিয়ে একটু আলগা করে রাখো । এখন

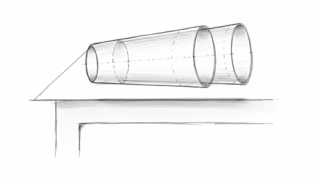
হাত পা দাঁত কিছু ব্যবহার না করে, সাঁড়াশি বা ক্লিপ বা কাঠি না-ঠেকিয়ে ভেতরের গেলাসটাকে বার করে আনতে পারবে ? টেবিলের ওপর দড়াম দড়াম করে ঘুষি মেরো না যেন!

.

48. হাতি-গলা ফাঁক

হলফ করে বলতে পারি, এ-র’ম সার্কাস তোমরা জীবনে দ্যাখোনি। একটা বেঁটেখাটো চেহারার লোক, ভীড় দেখে হাঁটুতে রীতিমতো কত্তাল বাজছে, সে কিনা আমাদের বেকুব বানিয়ে দিলো !

লোকটা পকেট-টকেট হাতড়ে একটা কাগজ বার করলো, স্কেল দিয়ে মেপে দ্যাখালো – 6″x6″, মাইকে ঘোষণা শোনা গেলো, লোকটা ঐ কাগজের মধ্যে দিয়ে নাকি সার্কাসের বিশাল হাতিটাকে গলিয়ে দেবে। লোকটা একটা কাঁচি দিয়ে কাগজটা কাটতে শুরু করলো। কাগজের গর্তটা যত বড়ো হয় আমাদের চোখও তত বড়ো হতে থাকে। কোনো আঠা আলপিনের ব্যাপার নেই, সেরেফ কাঁচি দিয়ে কাগজটা কেটে ট্র্যাপিজের তারে ঝুলিয়ে দিলো। আর হাতিটাও দিব্যি গজেন্দ্রগমনে তার ফাঁক দিয়ে গলে গেলো । তুমুল হাততালির মধ্যে লোকটা আরো নার্ভাস হয়ে নিজেও ঐ ফাঁকের মধ্যে দিয়ে গলে ভেতরে চলে গেলো ।

বাড়িতে গিয়ে দেখলুম, কাগজ কেটে হাতি-গলা ফাঁক আমিও করতে পারি । আশা করি তোমরাও পারবে।

.

49. লীলাময়বাবুর লীলাখেলা

বরযাত্রী গিয়ে এ কি দুর্দশা! তিরিশজন বরযাত্রী সেজেগুজে সেণ্ট– টেণ্ট মেখে (ছবি উঠবে তো!) বিকেল পাঁচটায় বাড়ি থেকে বেরিয়েছে। পাছে খিদে মরে যায় এই ভয়ে বিকেলের জলখাবার পর্যন্ত খায় নি। আর এখন রাত দশটা বাজতে চললো, খাবারের সাড়াশব্দ নেই। কনের মেসো লীলাময়বাবু ব্যস্তসমস্ত হয়ে সব যোগাড়-যস্তর করে দিচ্ছিলেন। কনের বাবার রাগ পড়লো তাঁর ওপর। তাঁর জন্যেই তো এই অনর্থ ঘটেচে। মাছ এসচে আটটার সময় । দই-মিষ্টি কবে আসবে কে জানে। লীলাময়বাবু কিন্তু নির্বিকার । ‘আর তো মিনিট পনেরোর ব্যাপার । ওটুকু সময় আমিই ম্যানেজ করে দিচ্চি। এমন খেলা দ্যাখাবো না, সব রাগ জল হয়ে যাবে ।” বলে একটা আস্ত দেশলাই বাক্স নিয়ে নিচে চলে গেলেন ।

বরযাত্রীদের দিকে দু হাত তুলে লীলাময়বাবু বললেন, ‘নমস্কার, দাদুরা । আমি হচ্চি কনের মেসো, আমার জন্যেই আপনাদের এত দুর্ভোগ। আমি আবার পুরনো দিনের চার্টার্ড অ্যাকাউন্টান্ট। হিসেবের গরমিল একদম সহ্য করতে পারি না। এই হিসেবের বাতিকের জন্য সমীকরণ ব্যাপারটা আমার খুব প্রিয়। অসমান জিনিস আমি একদম বরদাস্ত করি না। যেমন ধরুন, বলে পাখাটা নিভিয়ে, ফরাসের ওপর বসে, দেশলাই বাক্সটা খুলে কয়েকটা কাঠি সাজালেন ।

‘দেখতেই পাচ্ছেন’, লীলাময়বাবু প্রায় যাদুকরের মত হাত নেড়ে বললেন, ‘দুটো দিক সমান নয়। একটা কাঠি যে-কোনো দিক থেকে সরিয়ে যে-কোনো দিকে বসিয়ে দুটোদিক সমান করতে হবে । না হলে আমি সাবা রাত বিছানায় ছটফট করবো।’ সবাই খুব উৎসাহ

নিয়ে ঝুঁকে পড়লো, কিন্তু কারুরই মাথায় এলো না কী করে $\frac{XXII}{VIII}$ আর II-এর সমীকরণ করা যায়। লীলাময়বাবু এক মিনিট অপেক্ষা করে VIII-এর একটা কাঠি তুলে II-এর মাথায় বসিয়ে দিলেন। নিতবর পিন্টু, আনন্দে হাততালি দিয়ে উঠলো। ঠিক পরশুদিন ত্রিকোণমিতির ক্লাশে সে শিখেচে π –এর মান $\frac{22}{7}$ সে ধরে বসলো আরো খেলা দ্যাখাতে হবে।

বরের পিসে অবশ্য খুব একটা মজা পেয়েছেন বলে মনে হলো না।

ঘোৎ ঘোঁৎ করে তিনি বললেন, π = $\frac{22}{7}$ এটা কি সমীকরণ হলো ?

লীলাময়বাবু ব্যস্ত হয়ে বললেন, ‘না-না, এ একটা উদা’রণ দিলুম। এবার এইগুলো দেখুন তো। সব ঠিকঠাক আছে তো? বলে কাঠিগুলো তিনটে সারিতে সাজিয়ে বললেন, ‘একটা করে কাঠি সরিয়ে, আবার বসিয়ে দুটোদিক সমান করে দিন তো।’

.

.

.

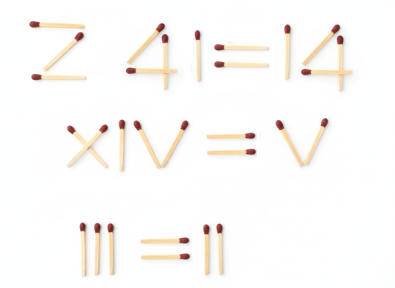
প্রথমটা পিন্টু, দ্বিতীয়টা বর, আর তৃতীয়টা বরের পিসে নিজেই করে দিলেন।

আশা করি তোমরাও এগুলো পারবে।

.

50. ভূতুড়ে গেঁট

একটা বড়ো রুমালের দুটো মুখ কোণাকুণি ধরো । এবার কোনো দিকের আঙুল না-ছেড়ে রুমালটার মধ্যেখানে একটা গেরো দিতে পারবে ? ধরার সময় যে-ভাবে ইচ্ছে ধরতে পারো, কিন্তু গেঁট দেয়ার সময় কোনো দিকের আঙুল ছাড়া চলবে না ।

.

51.সাংখ্যদর্শন

মানুষ কী করে গুনতে শিখলো বলা শক্ত । তবে প্রথম দফায় আমি আর তুমি, অর্থাৎ 1 আর 2-এর বেশি গোনা তার পক্ষে সম্ভব ছিল না। ‘অনেক‘ বা ‘প্রচুর‘ বোঝাতে তারা বলতো, “আমি-তুমি আমি-তুমি আমি-তুমি..‘। দুই হাঙ্গেরিয়ান বড়োমানুষের মধ্যে একবার বাজি হলো—কে সবচেয়ে বড়ো সংখ্যার নাম করতে পারে। প্রথমজন বললো, তিন। দ্বিতীয়জন বিস্তর মাথা চুলকেও তার চেয়ে বড়ো সংখ্যা বলতে পারলো না । শূন্য (0) আবিষ্কার করতে অনেক সময় লেগেচে । ভারত থেকেই আরবদের মারফৎ এটি ইওরোপে পৌঁছয়। সব মিলিয়ে সংখ্যার অসংখ্য বিন্যাস কিন্তু খুবই মজার।

123456789   987654321

12345678      87654321

1234567        7654321

123456           654321

12345              54321

1234                4321

123                   321

12                     21

1                       1

.

বলো তো, কোন্ দিকের যোগফলটা বড়ো হবে। সময় : পাঁচ সেকেণ্ড ।

এতে আর কী মজা! তাহলে ঘাথো: 123456789 × 8 +9 = 987654321. আর গুণই যদি করতে হয়:

0×9+1   = 1

1×9+2   = 11

12×9+3   = 111

123×9+4     = 1111

1234×9+5   = 11111

12345×9+6  = 111111

চললো অদ্বৈতের লীলা ।

বিয়োগ করলেও ঐ ব্যাপার।

9 8 7 6 5 4 3 2 1

1 2 3 4 5 6 7 8 9

___________________

8 6 4 1 9 7 5 3 2

1 থেকে 9 অবধি ঘুরে ফিরে সবাই আছে।

আবার গুণেই ফেরা যাক। শুধু ৪-টা বাদ দিয়েছি।

12345679×9=111111111

তেমনি   12345679

        999999999

_________________

12345678987654321

9-এর গুণিতক দিয়ে :

987654321 × 9=8888888889

            ×18=17777777778

            ×27=26666666667

            ×36=35555555556

            ×45=44444444445

            ×54=53333333334

           ×63=62222222223

            ×72=71111111112

            ×81=80000000001

আবার ভাগফল:

1÷9=0.1111111…

সাংখ্যদর্শন

2÷9=0.222222.

3÷9=0.333333…

8÷9=0.888888……

এবার ধাঁধায় আসা যাক। তিনটে 9 দিয়ে 10 লেখা খুবই সোজা । 9 + $\frac{9}{9}$ = 10. কিন্তু তিনটে 9 দিয়ে 20 লেখা যায় কী করে ? সব রকম পাটীগণিতচিহ্ন, অর্থাৎ যোগ-বিয়োগ-গুণ-ভাগ–দশমিক-পৌনঃ-পুনিক দশমিক-বর্গমূল-ঘনমূল-বন্ধনী সবই ব্যবহার করতে পারো ।

খুব শক্ত মনে হচ্ছে ? আচ্ছা। চারটে 4 দিয়ে 64 লেখা যায় কী করে? অতি সোজা কাজ:(4+4) × (4+4) । তিনটে 4 দিয়ে তো আরো সোজা, প্রায় জল: 4×4×4. কিন্তু যদি বলি দুটো 4 দিয়ে 64?

চারটে 4 দিয়ে 1, 2, 3, 4, 20 অবধি খুব সহজেই লেখা যায়, অবশ্য সব রকম পাটীগণিতচিহ্ন ব্যবহার করে । চারটে 2 দিয়ে 1 থেকে 20 অবধি লেখা যায় কী করে?

$\frac{22}{22}=1$ ; $\frac{2}{2}+\frac{2}{2}=2$ ; 2 + 2 – $\frac{2}{2}$ = 3; 2×2 + $\frac{2}{2}=5$ ; 2 × 2 + 2 + 2 = 8

এ তো করাই যায়।কিন্তু চারটে 2 দিয়ে 7, 17, 19 ? চেষ্টা করে দেখ। আর হ্যা, চারটে 2 দিয়ে বৃহত্তম সংখ্যা কী লেখা যায়— কোনো সংকেতচিহ্ন ব্যবহার না করে। 2222 নিশ্চয়ই নয়। তবে কি?

এ-র’ম আরো কতকগুলো দ্যাখো। পাটীগণিতের সব চিহ্ন ব্যবহার করতে পারো।

এক ৷৷ চারটে 1 দিয়ে 7

দুই ৷৷ দুটো 2 দিয়ে 32

তিন৷৷ তিনটে 3 দিয়ে 24

চার ৷৷ দুটো 5 দিয়ে 125

পাঁচ ৷৷ দশটা 6 দিয়ে 1000

ছয় ৷৷ পাঁচটা 7 দিয়ে 700

সাত ৷৷ দুটো ৪ দিয়ে 3

আর তিনটে প্রশ্নের উত্তর দাও:

আট৷৷ $4^{4^4}$ মোট ক-অংকের সংখ্যা?

নয় ৷৷ 1 থেকে 100-র মধ্যে ক-টা 9 আছে?

দশ ৷৷ 1000! (অর্থাৎ 1 × 2 × 3 ×…× 999 × 1000) —

সংখ্যাটার শেষে কতগুলো শূন্য থাকবে?

সংখ্যার আরো কিছু সমস্যা:

এগারো ৷৷ 60 থেকে 70 এর মধ্যে একটা সংখ্যা বলো, যাকে চার ভাগ করে প্রথম ভাগের সঙ্গে 3 যোগ করলে, দ্বিতীয় ভাগ থেকে 3 বিয়োগ দিলে, তৃতীয় ভাগকে 3 দিয়ে গুণ করলে ও চতুর্থ ভাগকে 3 দিয়ে ভাগ করলে একই ফল পাবে?

বারো৷৷ তিন সেকেণ্ডে মনে মনে গুণ করে।: 85×85 (এর একটা অতি সহজ কৌশল আছে)

তেরো৷৷ কাকেশ্বর কুচকুচের প্রশ্ন : 20-র $\frac{1}{4}$ যদি 6 হয়, তবে 10-এর $\frac{1}{3}$ কত হবে?

আবার 1 থেকে 9-এর মধ্যেই ঢোকা যাক ।

চোদ্দো৷৷ 1,3,5,7 আর 9—এই ক-টি বিজোড় সংখ্যা যোগ করলে যোগফল হয় 25, আর 2, 4, 6 আর ৪ – এদের যোগফল 20 এখন এই ক-টি সংখ্যাকে এমন ভাবে সাজিয়ে যোগ করো যাতে জোড় এবং বিজোড় সংখ্যার একই যোগফল হবে। জটিল বা বিদ্যুটে ভগ্নাংশ বা পৌনঃপুনিক দশমিক ব্যবহার করা চলবে না।

পনেরো ৷৷ 1 থেকে 9 অবধি সব ক-টা অংককে বাড়তি দিকে অর্থাৎ ascending order-এ লিখে যোগ করলে যোগফল হয় 45. এখন, ঐ ক-টি অংককে ঐ বাড়তির দিকে লিখে 45-এর নামতা সাজাতে পারো?

ষোলো ৷৷ খুঁজে পেতে এমন একটা সংখ্যা বার করতে পারো, যার বর্গ হবে ন-অংকের একটা সংখ্যা, যাতে 1 থেকে 9 অবধি সব ক-টা সংখ্যা একবার করে বসবে ?

সতেরো ৷৷ 1 থেকে 9 এই ন-টি অংককে যোগ করে যোগফল 100 করতে পারবে ? ( দশমিক ও পৌনঃপুনিক দশমিক ব্যবহার করা চলবে) ।

এবার 9-এর সঙ্গে আরেকটা অংক যোগ করা যাক–0.

আঠারো ৷৷ 1 থেকে 0 অবধি দশটি অংককে এমন দুটি ভগ্নাংশে সাজাও যার যোগফল হলে 1. কোনো অংক দুবার ব্যবহার করা চলবে না ।

ঊনিশ ৷৷ এবার ঐ দশটা অংককেই এমনভাবে দশমিকে সাজাও যার যোগফল হবে 1 (পৌনঃপুনিক চলতে পারে, কিন্তু কোনো অংক একবারের বেশি বসবে না) ।

কুড়ি ৷৷ 1 থেকে O-কে জোড়া করে করে সাজাও যাতে পাঁচটি জোড়ের প্রত্যেকটিই প্রথম জোড় দিয়ে বিভাজ্য হয় (যেমন,   14,28 ইত্যাদি। উত্তরটি কিন্তু অনন্য অর্থাৎ unique. কোনো অংক দুবার বসবে না)।

আদর্শ সংখ্যা বা Perfect number কাকে বলে জানো? যে– সংখ্যার গুণিতকগুলোর যোগফল সেই সংখ্যার সমান, আর গুণিতক– গুলোর বিপরীত বা reciprocal-এর (মূল সংখ্যাটির বিপরীত সুদ্ধ) যোগফল সর্বদাই 2, তাদেরই বলে আদর্শ সংখ্যা ।সবচেয়ে ছোট আদর্শ সংখ্যা 6 (1+2+3=6, $\frac{1}{1}$ + $\frac{1}{2}$ + $\frac{1}{3}$ + $\frac{1}{6}$ = $\frac{12}{6}$ = 2) | তার ঠিক পরেই আদর্শ সংখ্যা কোন্‌টা?

একুশ ৷৷ 1 থেকে 9 অবধি সব ক-টা অংক এমন ভাবে ভগ্নাংশে লেখো যার ভাগফল 9 হবে। কোনো অংক দুবার বসানো চলবে না।

বাইশ ৷৷ 1 থেকে 9 দিয়ে চারটে বর্গ সংখ্যা তৈরি করো, একই অংক দুবার ব্যবহার না-করে ।

তেইশ ৷৷ পাঁচটা বিজোড় অংক বা figure যোগ করে যোগফল 14 করতে পারো?

চব্বিশ ৷৷ সবচেয়ে ছোটো কোন্ সংখ্যার কথা ভাবতে পারো যাকে 10 দিয়ে ভাগ করলে 9, 9 দিয়ে ভাগ করলে 8, 2 দিয়ে ভাগ করলে 1 ভাগশেষ থাকবে?

.

চারটে 5 দিয়ে 100 লেখা খুব সোজা: (5+5) × (5+5). চারটে 9 দিয়েও শক্ত নয়: 99+$\frac{9}{9}$

কিন্তু চারটে 7 দিয়ে 100 পাটীগণিতের সব চিহ্ন ব্যবহার করতে পারো ।

পঁচিশ ৷৷ 48 সংখ্যাটা খুব অদ্ভুত । এর সঙ্গে 1 যোগ করে 49, অর্থাৎ 7-এর বর্গ । তেমনি 48-এর আদ্ধেক 24, তার সঙ্গে 1 যোগ করলেও আরেকটা বর্গ সংখ্যা পাওয়া যাচ্ছে। এ-র’ম অদ্ভুত সংখ্যার অবশ্য কোনো শেষ নেই। কিন্তু 48- এর ঠিক পরেই কোন্ সংখ্যার এই গুণ আছে, বলতে

পারো?

ছাব্বিশ ৷৷ এবার একটা শূন্যস্থান পূরণের ব্যাপার ।

123456789 = 100.1 আর 2, 2 আর 3… 8 আর 9-এর মধ্যে যে-ফাঁকগুলো আছে, সেখানে স্রেফ যোগচিহ্ন (+) আর সেটাকে 45° ঘোরালে যা হয়, অর্থাৎ গুণচিহ্ন (×) বসিয়ে সমীকরণটা মিলিয়ে দাও। এটা যদি পারো তা’লে এবার যোগচিহ্ন, বিয়োগচিহ্ন আর প্রথম বন্ধনী দিয়ে শূন্যস্থান পূরণ করো। দেখো, সমীকরণটা যেন মেলে ৷

.

52. ধাঁধালি

১। এক ভদ্রলোক খুব ক্লান্ত হয়ে রাত দশটায় ঘুমোতে গেলেন।পাছে বেশি ঘুমিয়ে পড়েন তার জন্যে পরের দিন এগারোটায় অ্যালার্ম দিয়ে ঘড়িটা খাটের পাশে রাখলেন। অ্যালার্মের আওয়াজে তাঁর ঘুম ভাঙলো। ভদ্রলোক ক-ঘণ্টা ঘুমিয়েছেন?

২। ইন্টারভিউ দিতে গ্যাচে দুই ভাই। দ্যাখা গেলো, তাদের বয়েস এক, বিকম পাশ করেছে একই বছরে, বাবা-মার নাম এক, বাড়ির ঠিকানা এক। জিগেস করা হলো: আপনারা কি যমজ? দুজনেই বলল, না স্যার। তাহলে তাদের সম্পর্কটা কী?

৩৷ অন্ধকার ঘরে ঢুকলুম। লোড শেডিং। জানি, ঘরের মধ্যে একটা হ্যারিকেন, একটা লম্ফ, যার একটা মোমবাতি আছে। পকেট হাতড়ে দেখি দেশলাই বাক্সে একটাই মাত্র কাঠি রয়েছে। আগে কোন্‌টা জ্বালবো?

৪। কোন, কথাটা সব মাস্টারমশাই ভুল উচ্চারণ করেন?

৫। অংকে লেখো : ন হাজার নশ নিরানব্বই, বারো হাজার বারোশ বারো

৬। বছরের ক-টা মাসে তিরিশ দিন আছে?

৭। সব খেলায় প্রথমে এলে ফার্স্ট হয়। কোন্ খেলায় ফার্স্ট হবে সবার শেষে এলে ?

৮। কাটলে একটা, না কাটলে দুটো। জিনিসটা কী ?

৯। 50-কে 1⁄2 দিয়ে ভাগ করে 3 যোগ করলে কত হয় ?

১০। একটা দড়ির দৈর্ঘ্য কত ?

১১। টেলিফোনে কোন নম্বর ডায়াল করলে সর্বদাই পিপ, পিপ্‌ পিপ্‌ অর্থাৎ এনগেজড টোন পাবেই?

১২। একটা অ্যাকুয়ারিঅম-এ তেরোটা মাছ ছিল। তার চারটে গেলো মরে। কটা রইল ?

১৩। শূন্যস্থান পূরণ করোঃ বাবর হুমায়ুনের বাবা,বাবর হুমায়ুনের বাবার……।

১৪। 10’ × 10’ × 10’ গর্ত খুঁড়তে যদি 10 টাকা মজুরি হয়, 5′ × 5‘ × 5′ গর্ত খুঁড়লে কত মজুরি হবে?

১৫। তিনটে বেড়ালের তিনটে ইঁদুর খেতে যদি তিন সেকেণ্ড সময় লাগে, তবে একশটা বেড়ালের একশটা ইঁদুর খেতে কত সময় লাগছে?

১৬। দেশ আছে মাটি নেই, শহর আছে মানুষ নেই, সাগর আছে জল নেই—ব্যাপারটা কী ?

১৭। সেদিন একটা দোকানে অদ্ভুত প্রশ্নোত্তর শুনলুম।

–একটার দাম কত?

–কুঁড়ি পয়সা।

–বাইশটা?

–চল্লিশ পয়সা ।

আমি দুশ তেইশটা নোবো। কত পড়বে?

–ষাট পয়সা ।

দোকানটায় কী বিক্রি হয়?

১৮। যুধিষ্ঠিরের উদ্দেশ্যে বকরূপী যক্ষ তথা ধর্মের অপ্রকাশিত

প্রশ্নঃ ষণ্ড কখন হর্যক্ষের মাংস ভক্ষণ করে?

১৯। 25–এই সংখ্যাটি থেকে ক-বার 1 বিয়োগ করা যায়?

২০। দুটো ঘড়ি, একটা রোজ পাঁচ মিনিট শ্লো যায়, অন্যটা একদম চলেই না। কোন্ টা ভালো সময় দেবে?

২১৷ দুটো মুরগী দুদিনে দুটো ডিম পাড়লে, ছ-টা মুরগী ছ-দিনে ক-টা ডিম পাড়বে?

২২৷ আমার পোলট্রিতে ছিল সতেরোটা হাঁস ৷ ন-টা বাদে সব ক-টাই শেয়ালে নিয়ে গেলো। ক-টা হাঁস রইল?

২৩। অমাবস্যা তিথি। আপাদমস্তক কালো র‍্যাপার মুড়ি দিয়ে একটা লোক রাস্তা পার হচ্চে। এমন সময় একটা কালো অ্যাম্বাসাডার তীর বেগে তার দিকে ছুটে এলো। রাস্তায় কোনো ল্যাম্পপোস্ট নেই । গাড়ির হেডলাইটও নেভানো। গাড়িটা ঠিক তাকে পাশ কাটিয়ে বেরিয়ে গেলো। ড্রাইভার নাকি লোকটাকে দেখতে পেয়েছিল। কী করে দেখলো?

২৪। ডিলাক সিং এক মাইল ছোটে 5:17 মিনিটে, রিলাক সিং 5.17 মাইল ছোটে এক ঘণ্টায় ৷ কে বেশি জোরে ছোটে?

২৫। লিলি পাখি বসে ছিল সারা ছাদ জুড়ে

ডড পাখি ফস্ করে চলে গেলো উড়ে।

কত পাখি সেই ছাদে রয়ে গেলো পড়ে?

২৬। একটা সিংহ বনের মধ্যে কতদূর ঢুকতে পারে?

২৭। হাতের বুড়ো আঙুল আর কড়ে আঙুলের মধ্যে কতখানি তফাৎ?

২৮। যদ্দিন বেকার ছিলুম, ছিলুম। এখন এক সঙ্গে দুটো চাকরি পেয়েছি। একটার মাইনে বছরে 1000 টাকা, বছরের শেষে 200 টাকা ইনক্রিমেন্ট। অন্যটার মাইনে ছ মাসে 500 টাকা, আর ছ মাস অন্তর 50 টাকা ইনক্রিমেন্ট। কোনটা নি, বলো তো?

২৯। গজু বাড়ির দরজায় দাঁড়িয়ে এক মনে গুনচে তাদের গলি দিয়ে কত লোক যায়। ভজুও তাই করছে, রাস্তায় পায়চারি করতে করতে। কে বেশি লোক গুনবে ?

৩০। রাস্তায় প্যাচপ্যাচে কাদা। তুলসী দুপা এগোয় তো তিন পা পেছোয় । ও এখন ইস্কুলে পৌছবে কী করে?

৩১। চায়ের দোকানে তিন ভদ্রলোক বসে তিনটি ডবল হাফ চায়ের অর্ডার দিলেন। তিনজনকেই চিনি। একজন বিবাহিত, একজন বিপত্নীক, আরেকজন বিয়েই করেন নি। চা এলো । প্রথম ভদ্রলোক দেখি ঘড়ির কাঁটা মাফিক (clockwise), দ্বিতীয়জন তার উল্টো কায়দায় (anti-clockwise) আর তৃতীয়জন এলোমেলো ভাবে কাপের মধ্যে চামচ নাড়ছেন । কেন?

৩২। একটা হাঁসের সামনে দুটো হাঁস, দুটো হাঁসের পেছনে একটা হাঁস, আর মধ্যেখানে একটা—কমপক্ষে ক-টা হাঁস থাকলে এটা হতে পারে ।

৩৩। টানলে সাধারণত সব জিনিস হয় বাড়ে, নয় যেমন ছিল তেমনি থাকে। টানলে ছোটো হয় কোন জিনিস?

৩৪। চা-এর কাপের হাতল কোন দিকে থাকে?

৩৫। হাইপো-বোটানিক্যাল গার্ডেনে চড়ুইভাতি।দুটো এক চেহারার কাপে সমান পরিমাণ জল রয়েছে। একটায় তাপ 4 সেন্টিগ্রেড, অন্যটায় 4 ফারেনহাইট। একই সঙ্গে একই ওজনের দুটো ডিম একই উচ্চতা থেকে দুটো কাপেই ফ্যালা হলো।কোন্ কাপের ডিমটা আগে তলায় পড়বে?

৩৬। ইংরিজিতে মোট পাঁচটা স্বরবর্ণঃ a, e, i, o, u. এদের কেউ-না-কেউ না-থাকলে কোনো শব্দ উচ্চারণ করাই শক্ত। একই শব্দে এঁদের দু-তিনজনও হাজির থাকেন । এমন পাঁচটা শব্দ বলতে পারো যাতে এঁরা পাঁচজনেই একবার করে উপস্থিত আছেন?

৩৭। কাটলে সাধারণত সব জিনিসই আকারে ছোটো হয়ে যায়, কিন্তু সংখ্যায় বাড়ে। কাটলে আকারে বাড়ে কিন্তু সংখ্যায় কমে না কোন জিনিস?

৩৮। কলকাতার কোন রাস্তায় 120 নম্বর বাস চলে?

৩৯। একটা গোল টিনে 50টা সিগারেট ধরে। এখন টিনের ব্যাসটা যদি বাড়িয়ে ছগুণ করা হয়, কত সিগারেট ধরবে?