সামান্তরিক উপপাদ্য
(Parallelogram Theorem)
উপপাদ্য 20 (Theorem 20)
বিবৃতি (Statement):
সামান্তরিকের বিপরীত বাহুগুলি সমান, বিপরীত কোণগুলি সমান এবং প্রত্যেক কর্ণ সামান্তরিককে দুইটি সর্বসম ত্রিভুজে বিভক্ত করে।[The opposite sides and angles of a parallelogram are equal, and each diagonal divides the parallelogram into two congruent triangles. Euc. I. 34. ]
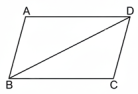
ABCD একটি সামান্তরিক BD একটি কর্ণ।
প্রমাণ করিতে হইবে যে,
(1) AD=BC, AB=DC; (2) ∠BAD=∠BCD
(3) ∠ABC=∠ADC এবং (4) △BAD ≅ △BCD।
প্রমাণ। AD ও BC সমান্তরাল এবং BD উহাদের সহিত মিলিত হইয়াছে।
∴ ∠ADB = একান্তর ∠DBC।
আবার, AB ও DC সমান্তরাল এবং BD উহাদের সহিত মিলিত হইয়াছে,
∴ ∠ABD = একান্তর ∠BDC।
অতএব, △BAD ও △BCD ত্রিভুজ দুইটির
∠ADB=∠DBC, ∠ABD=∠BDC এবং BD=BD;
∴ ত্রিভুজ দুইটি সর্বসম। . . . (4) (স্বতঃ 6)
∴ AD=BC, AB=DC . . . (1)
∠BAD=∠BCD . . . (2)
আবার, ∠ABD=∠BDC এবং ∠DBC=∠ADB; (প্রমাণিত)
∴ সমগ্র ∠ABC=সমগ্র ∠ADC। . . . (3)
উপপাদ্য 21 (Theorem 21)
বিবৃতি (Statement):
সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে।
[The diagonals of a parallelogram bisect one another.]
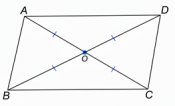
ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করিয়াছে।
প্রমাণ করিতে হইবে যে, OA = OC এবং OD = OB।
প্রমাণ। AD ও BC সমান্তরাল এবং BD উহাদের সহিত মিলিত হইয়াছে,
∴ ∠ODA = একান্তর ∠OBC (উপ. 3)
আবার, AD ও BC সমান্তরাল এবং AC উহাদের সহিত মিলিত হইয়াছে,
∴ ∠OAD = একান্তর ∠OCB (উপ. 3)
অতএব △AOD ও △BOC ত্রিভুজ দুইটির
∠ODA = ∠OBC, ∠OAD = ∠OCB এবং AD = BC;
∴ ত্রিভুজ দুইটি সর্বসম। (স্বতঃ 6)
∴ OA = OC এবং OD = OB।
অনুসিদ্ধান্ত : রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।[The diagonals of a rhombus bisect one another at right angles.]
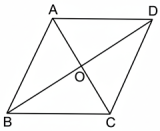
ABCD রম্বসের কর্ণদ্বয় O বিন্দুতে ছেদ করিয়াছে।
প্রমাণ। △AOD ≅ △BOC (স্বতঃ 6)
∴OA = OC এবং OD = OB।
আবার, △ABO ≅ △ADO (উপ. 11)
∴ ∠AOB = ∠AOD। কিন্তু উহারা সন্নিহিত কোণ বলিয়া প্রত্যেকে সমকোণ;
∴ AC ও BD পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
উপপাদ্য 22 (Theorem 22)
বিবৃতি (Statement):
যে চতুর্ভুজের বিপরীত বাহুগুলি সমান, তাহা একটি সামান্তরিক।
[A quadrilateral is a parallelogram if both pairs of its opposite sides are equal.]
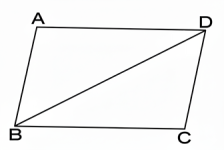
ABCD চতুর্ভুজ-এর AB = CD এবং AD = BC।
প্রমাণ করিতে হইবে যে, ABCD একটি সামান্তরিক।
BD যোগ কর
প্রমাণ। BAD ও BCD ত্রিভুজ দুইটির
AB = CD,
AD = BC (কল্পনা)
এবং BD = BD;
∴ ত্রিভুজ দুইটি সর্বসম। (উপ. 11)
∴ ∠ABD = ∠BDC;
কিন্তু ইহারা একান্তর কোণ; …(i)
∴ AB ও CD সমান্তরাল (উপ. 2)
এবং ∠ADB = ∠DBC;
কিন্তু ইহারা একান্তর কোণ;
∴ AD ও BC সমান্তরাল। (উপ. 2)
অতএব ABCD চতুর্ভুজ-এর
AB || CD এবং AD || BC;
∴ ABCD একটি সামান্তরিক।
উপপাদ্য 23 (Theorem 23)
বিবৃতি (Statement):
যে চতুর্ভুজ-এর বিপরীত কোণগুলি সমান, তাহা একটি সামান্তরিক।
[A quadrilateral is a parallelogram if both pairs of its opposite angles are equal.]
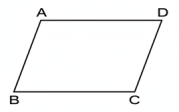
ABCD চতুর্ভুজ-এর ∠A = ∠C এবং ∠B = ∠D।
প্রমাণ করিতে হইবে যে, ABCD একটি সামান্তরিক।
প্রমাণ। যেহেতু, ∠A = ∠C এবং ∠B = ∠D; (কল্পনা)
∴ ∠A + ∠B = ∠C + ∠D,
∴ ∠A + ∠B = 12 (∠A + ∠B + ∠C + ∠D)
= 12 × 4 সমকোণ = 2 সমকোণ।
কিন্তু ∠A ও ∠B, AB-এর একই পার্শ্বস্থ অন্তঃস্থকোণ;
∴ AD এবং BC সমান্তরাল। (উপ. 2)
আবার, ∵ ∠A = ∠C এবং ∠D = ∠B,
∴ ∠A + ∠D = ∠C + ∠B,
∴ ∠A + ∠D = 12 (∠A + ∠D + ∠C + ∠B)
= 12 × 4 সমকোণ = 2 সমকোণ;
কিন্তু ∠A ও ∠D, AD-এর একই পার্শ্বস্থ অন্তঃস্থকোণ;
∴ AB এবং DC সমান্তরাল। (উপ. 2)
অতএব, ABCD চতুর্ভুজের
AD || BC এবং AB || DC;
∴ ABCD একটি সামান্তরিক।
উপপাদ্য 24 (Theorem 24)
বিবৃতি (Statement):
যে চতুর্ভুজ-এর দুইটি বিপরীত বাহু সমান ও সমান্তরাল, তাহা একটি সামান্তরিক।
[A quadrilateral is a parallelogram if one pair of its opposite sides are equal and parallel.]
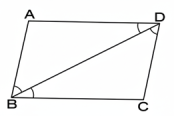
ABCD চতুর্ভুজ-এর AD ও BC সমান ও সমান্তরাল।
প্রমাণ করিতে হইবে যে, ABCD একটি সামান্তরিক।
BD যোগ কর।
প্রমাণ। AD ও BC সমান্তরাল এবং BD উহাদের সহিত মিলিত হইয়াছে,
∴ ∠ADB = একান্তর ∠CBD। (উপ. 3)
অতএব, ADB ও CBD ত্রিভুজ দুইটির
AD = BC, (কল্পনা)
BD = BD
এবং অন্তর্গত ∠ADB = অন্তর্গত ∠CBD;
∴ ত্রিভুজ দুইটি সর্বসম। (স্বতঃ 5)
∴ ∠ABD = ∠CDB। কিন্তু ইহারা একান্তর কোণ,
∴ AB ও DC সমান্তরাল। (উপ. 2)
অতএব, ABCD চতুর্ভুজ-এর AD || BC এবং AB || DC,
∴ ABCD একটি সামান্তরিক।
অনুসিদ্ধান্ত।দুইটি সরলরেখা সমান ও সমান্তরাল হইলে, উহাদের একই পার্শ্বস্থ দুই প্রান্তবিন্দু সংযোগকারী সরলরেখা অপর দুই প্রান্তবিন্দু সংযোগকারী সরলরেখার সমান ও সমান্তরাল হইবে।
[ কারণ, উপরের চিত্রে দেওয়া ছিল, AD ও BC সমান ও সমান্তরাল এবং প্রমাণিত হইয়াছে AB || DC এবং △ADB ≅ △CBD বলিয়া AB = DC। ]
উপপাদ্য 25
বিবৃতি (Statement):
যে চতুর্ভুজ-এর কর্ণদ্বয় পরস্পরকে সমদ্বিখণ্ডিত করে, তাহা একটি সামান্তরিক।
[A quadrilateral is a parallelogram if its diagonals bisect one another.]
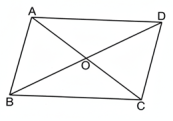
ABCD চতুর্ভুজ-এর AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে সমদ্বিখণ্ডিত করিয়াছে।
প্রমাণ করিতে হইবে যে, ABCD একটি সামান্তরিক।
প্রমাণ।AOD ও BOC ত্রিভুজ দুইটির
OA = OC, OD = OB (কল্পনা)
এবং ∠AOD = বিপ্রতীপ ∠COB (স্বতঃ 5)
∴ ত্রিভুজ দুইটি সর্বসম।
∴ AD = BC, এবং ∠OAD = ∠OCB,
কিন্তু ইহারা একান্তর কোণ, ∴ AD || BC; (উপ. 2)
∴ AD ও BC সমান ও সমান্তরাল;
∴ ABCD একটি সামান্তরিক (উপ. 24)
অনুশীলনী 57
(উপ. 20-25 বিষয়ক)
1. সামান্তরিকের একটি কোণ সমকোণ হইলে উহার সকল কোণই সমকোণ হইবে; অর্থাৎ আয়তক্ষেত্রের সকল কোণ
2. আয়তের দুইটি সন্নিহিত বাহু সমান হইলে, উহার সকল বাহু সমান হইবে।
3. বর্গক্ষেত্রের সকল কোণ সমকোণ এবং সকল বাহু সমান।
4. রম্বস একটি সামান্তরিক। রম্বসের বিপরীত কোণগুলি সমান।
5. একই ভূমির বিপরীত পার্শ্বে অবস্থিত দুইটি সামান্তরিকের ক্ষেত্রফল তুল্য, তাহা একটি সামান্তরিক উপর অঙ্কিত।
6. সামান্তরিকের যে কোন বাহুসংলগ্ন কোণদ্বয়ের সমদ্বিখণ্ডক সম্পূর্ণ উপরে করে।
7. কোন আয়তক্ষেত্রের বাহুগুলির মধ্যবিন্দু যোগ করিলে যে চতুর্ভুজ উৎপন্ন হয়, তাহা একটি রম্বস।
8. ABCD সামান্তরিকের AC কর্ণ যদি ∠A কে সমদ্বিখণ্ডিত করে, তবে উহা ∠C কেও সমদ্বিখণ্ডিত করিবে এবং সামান্তরিকটি একটি রম্বস হইবে।
9. রম্বসের কর্ণ যে দুইটি কোণের মধ্য দিয়া গমন করে, তাহাদিগের সমদ্বিখণ্ডিত করে।
10. কোন সামান্তরিকের কর্ণদ্বয় যদি সমান হয়, তবে উহার সকল কোণই সমকোণ এবং উহা একটি আয়ত।
11. দুইটি সমান্তরাল সরলরেখার ব্যবধান সর্বত্র সমান।
[ ইঙ্গিত : একটি রেখার যে কোন দুই বিন্দু হইতে অপরটির উপর লম্ব টান। এখন দেখাও যে, ওই লম্বদ্বয় একটি সামান্তরিকের বিপরীত বাহু ]
12. বর্গক্ষেত্রের কর্ণদ্বয় পরস্পর সমান।
13. আয়তক্ষেত্রের কর্ণদ্বয় পরস্পর সমান।
14. বর্গক্ষেত্রের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে।
15. কোন সামান্তরিকের একটি কর্ণের মধ্যবিন্দু দিয়া উহার দুইটি বিপরীত বাহু পর্যন্ত অঙ্কিত সরলরেখা ঐ মধ্যবিন্দুতে সমদ্বিখণ্ডিত হইবে।
[ কারণ, উৎপন্ন ত্রিভুজ দুইটি সর্বসম ]
16. রম্বসের কর্ণদ্বয় রম্বসকে চারিটি সর্বসম ত্রিভুজে বিভক্ত করে।
17. কোন সামান্তরিকের কর্ণদ্বয় বিপরীত দুই দুই বাহুর মধ্যবিন্দু যোগ করিলে যে চারিটি চতুর্ভুজ উৎপন্ন হয়, তাহাদের প্রত্যেক একটি একটি সামান্তরিক।
18. সামান্তরিকের কোণগুলির সমদ্বিখণ্ডকগুলি একটি আয়তক্ষেত্র উৎপন্ন করে।
[ প্রশ্ন 6 এর সাহায্যে প্রমাণ কর ]
19. ABCD একটি সামান্তরিক এবং L ও M যথাক্রমে AB ও CD-র মধ্যবিন্দু। প্রমাণ কর যে, ALMD একটি সামান্তরিক।
20. ABCD একটি সামান্তরিক। P ও Q যথাক্রমে AB ও CD-র উপর দুইটি বিন্দু। যদি AP = CQ হয়, তবে BPDQ একটি সামান্তরিক।
21. ABC ও XYZ ত্রিভুজদ্বয়ের AB ও BC যথাক্রমে XY ও YZ এর সমান ও সমান্তরাল। প্রমাণ কর যে, AO ও XZ পরস্পর সমান ও সমান্তরাল।
[ ইঙ্গিত :
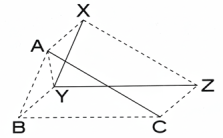
AX, BY, CZ যোগ কর ।
এখন, AB ও XY সমান ও সমান্তরাল,
∴ AX ও BY সমান ও সমান্তরাল।
আবার, BC ও YZ সমান ও সমান্তরাল
∴ BY ও CZ সমান ও সমান্তরাল।
∴ AX ও CZ সমান ও সমান্তরাল।
∴ AC ও XZ সমান ও সমান্তরাল।]
22. ABCD সামান্তরিকের E, F, G ও H যথাক্রমে AB, BC, CD ও DA-র উপর অবস্থিত বিন্দু। যদি AE = CG এবং AH = FC হয়, তবে EFGH একটি সামান্তরিক।
[ ইঙ্গিত :
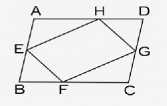
△AEH ≅ △CGF (স্বতঃ 5)
∴ EH = FG।
এইরূপ, EF = HG; ইত্যাদি ]
23. ABCD সামান্তরিকের অন্তর্ভুক্ত O যে কোন বিন্দু। OAEB, OBFC, OCGD ও ODHA সামান্তরিকগুলি অঙ্কিত করিয়া প্রমাণ কর যে, EFGH একটি সামান্তরিক।
[ ইঙ্গিত:
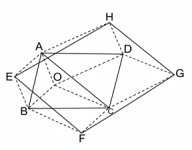
AC যোগ কর।
এখন, AH ও CG, OD-র সমান ও সমান্তরাল।
∴ HG, AC-র সমান ও সমান্তরাল।
এইরূপ, EF, AC-র সমান ও সমান্তরাল।
∴ HG ও EF সমান ও সমান্তরাল।
∴ EFGH একটি সামান্তরিক।]
24. ABCD ও ABEF সামান্তরিকদ্বয়ের AB সাধারণ বাহু। প্রমাণ কর যে, CDFE একটি সামান্তরিক।
[ কারণ, DC ও FE, AB-র সমান ও সমান্তরাল ]
25. কোন ত্রিভুজ-এর ভূমিসংলগ্ন কোণদ্বয়ের সমদ্বিখণ্ডকদ্বয় সমান হইলে ত্রিভুজটি সমদ্বিবাহু হইবে।
[If the bisectors of the base angles of a triangle are equal, then the triangle is isosceles.]
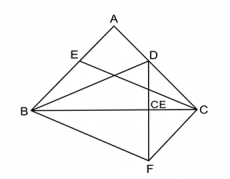
ABC ত্রিভুজ-এর B ও C কোণের সমদ্বিখণ্ডক
BD = CE
প্রমাণ করিতে হইবে যে, AB = AC।
B হইতে EC-র সহিত সমান ও সমান্তরাল করিয়া BF টান। DF ও CF যোগ কর।
প্রমাণ। যদি AB = AC না হয়, তবে মনে
করি AB > AC। তাহা হইলে ∠C > ∠B।
∵ ∠BEC = ∠A + 12 ∠C
এবং ∠BDC = ∠A + 12∠B,
∴ ∠BEC > ∠BDC।
কিন্তু ∠BEC = ∠BFC [ ∵ ▱ BECF এর বিপরীত কোণ ]
∴ ∠BFC > ∠BDC …(1)
আবার, BF = EC = BD,
∴ ∠BFD = ∠BDF … (2)
∴ (1) হইতে (2) বাদ দিয়া, ∠CFD > ∠CDF,
∴ CD > CF; অর্থাৎ CD > BE।
এখন, DBC ও ECB ত্রিভুজদ্বয়ের
BD = CE, BC = BC এবং CD > BE (উপ. 18)
∴ ∠DBC > ∠ECB
∴ ∠ABC > ∠ACB, ∴ AC > AB; কিন্তু ইহা কল্পনাবিরুদ্ধ।
∴ AB ও AC অসমান নহে; অর্থাৎ AB = AC।
