ক্ষেত্রফল
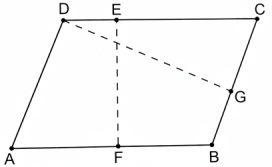
113. সামান্তরিকের যে কোন বাহুকে ভূমি বলিয়া ধরা যায়। সামান্তরিকের ভূমির বিপরিত বাহুর যে কোন বিন্দু হইতে ভুমির উপর অঙ্কিত লম্বকে উহার উন্নাতি বা উচ্চতা (Altitude or height) বলে।
পার্শ্বস্থ চিত্রে, ABCD সামান্তরিকের AB কে ভূমি ধরিলে EF লম্ব উহার উচ্চতা এবং BC কে ভূমি ধরিলে DG লম্ব উহার উচ্চতা।
114. (a) যে সকল ত্রিভুজ বা সামান্তরিক একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত, তাহাদের উচ্চতা পরস্পর সমান।
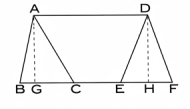
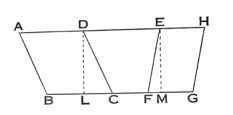
প্রথম চিত্র দ্বিতীয় চিত্র
প্রথম চিত্রে, ABC ও DEF ত্রিভুজদ্বয় AD ও BF সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত। এস্থলে AD || BF এবং AG ও DH যথাক্রমে A ও D হইতে BF এর উপর লম্ব। ∴ AGHD একটি আয়তক্ষেত্র; ∴ AG = DH
দ্বিতীয় চিত্রে, ABCD ও EFGH সামান্তরিকদ্বয় AH ও BG সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত এবং DL ও EM, BGর উপর লম্ব। এস্থলে DLME একটি আয়তক্ষেত্র; ∴ DL = EM
(b) যে সকল ত্রিভুজ বা সামান্তরিক উচ্চতা সমান,তাহাদিগকে দুইটি সরলরেখাদ্বয়ের মধ্যে স্থাপিত করা যায়।
প্রথম চিত্রে, মনে কর যেন AG = DH। উহারা BF এর উপর লম্ব বলিয়া পরস্পর সমান্তরালও বটে।
∴ AD || GH, অর্থাৎ AD || BF। (উপ. 24)
দ্বিতীয় চিত্রে, মনে কর যেন DL = EM। উহারা BGর উপর লম্ব বলিয়া পরস্পর সমান্তরালও বটে।
∴ DE || LM, অর্থাৎ AH || BG। (উপ. 24)
115. একই ভূমির উপর এবং একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত (অথবা, একই উচ্চতাবিষ্ট) সামান্তরিকসমূহের ক্ষেত্রফলের পরস্পর সম্বন্ধ নির্ণয়।
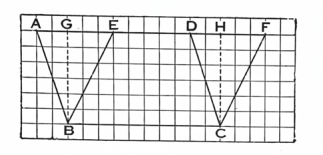
ছক–কাগজে চিত্রর ন্যায় একই ভূমি BCর উপর এবং একই BC ও AF সমান্তরাল সরলরেখাদ্বয়ের মধ্যে ABCD ও EBCF সামান্তরিকদ্বয় আঁক। উহারা একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত বলিয়া উহারা একই উচ্চতাবিষ্ট [অনু. 114 (a) দেখ]।
BGHC আয়তটি আঁক।
চিত্র , ▱ ABCD = △AGB + ▭ BGHC – △DHC … (1)
এখন, দেখ, △AGB = ½BG.AG = ½ × .6 × .2 ব. ই. = ।06 ব. ই., (অনু. 79)
▭ BGHC = BC.BG = 1 × 6 ব. এ. = 6 ব. ই., (অনু. 74)
এবং △DHC = ½CH.DH = ½ × 6 × 2 ব. ই., = 06 ব. ই., (অনু. 79)
(1) হইতে, □ABCD = (06 + 6 – 06) ব. ই., = 6 ব. ই.,
আবার চিত্র দেখ, △EBCF = △FHC + ▭ CHGB – △EGB … (2)
এখন দেখ, △FHC = ½CH.FH = ½ × .6 × .3 ব. ই., = 09 ব. ই.,
▭ CHGB = BC.CH = 1 × .6 ব. ই., = .6 ব. ই.,
এবং △EGB = ½BG.EG = ½ × 6 × 3 ব. ই., = 09 ব. ই.,
∴ (2) হইতে, ▭ EBCF = (.09 + .6 – .09) ব. ই., = 6 ব. ই.,
তাহা হইলে ABCD ও EBCF সামান্তরিকদ্বয়ের ক্ষেত্রফল সমান হইল।
অতএব সিদ্ধান্ত হইল:
সিদ্ধান্ত। একই ভূমির উপর এবং একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত (অথবা, একই উচ্চতাবিষ্ট) সামান্তরিকসমূহের ক্ষেত্রফল পরস্পর সমান।
মন্তব্য। 79 অনুচ্ছেদে প্রদত্ত দ্বিতীয় প্রণালী অনুসারে ছোট বর্গক্ষেত্রগুলি গণিয়া ত্রিভুজগুলীর ক্ষেত্রফল নির্ণয় করা চলিত কিন্তু তাহাতে উহাদের ক্ষেত্রফল সঠিকভাবে নির্ণয় করা দুরূহ হইত।
প্রশ্ন। ভূমি যথাক্রমে 1″.2″, 1″.4″, 1″.5″, 1″.8″ ও 2″ এবং উচ্চতা যথাক্রমে 6″, 8″, 1″, 1″.2″ ও 1″.5″ লইয়া ছক–কাগজে দুইটি করিয়া সামান্তরিক আঁক। প্রত্যেক স্থলে সামান্তরিকদ্বয়ের ক্ষেত্রফল সমান কিনা পরীক্ষা করিয়া দেখ।
উপপাদ্য 29
একই ভূমির উপর এবং একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত সামান্তরিকগুলির ক্ষেত্রফল পরস্পর সমান।[ Parallelograms on the same base and between the same parallels are equal in area. Euc. I. 35. ]
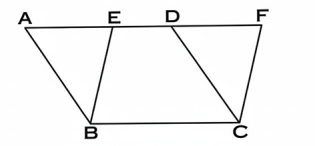
ABCD ও EBCF সামান্তরিকদ্বয় একই ভূমি BCর উপর এবং একই BC ও AF সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত।
প্রমাণ করিতে হইবে যে, ▱ ABCD ক্ষেত্রফল = ▱ EBCF এর ক্ষেত্রফল।
প্রমাণ। EAB ও FDC ত্রিভুজদ্বয়ের
∠EAB = অনুরূপ ∠FDC (∵ AB || DC)
∠AEB = অনুরূপ ∠DFC (∴ EB || FC)
AB=DC (∵ ▱ ABCDর বিপরীত বাহুদ্বয়)
∴ △EAB = △FDC। (স্বতঃ 6)
∴ চতুর্ভুজ ABCF – △FDC = চতুর্ভুজ ABCF – △EAB;
∴ ▱ ABCDর ক্ষেত্রফল = ▱ EBCF এর ক্ষেত্রফল।
অনুসিদ্ধান্ত 1. একই ভূমি ও সমান সমান উচ্চতাবিষ্ট সামান্তরিকের ক্ষেত্রফল পরস্পর সমান।
[ Parallelograms on the same base and of equal altitudes are equal in area.
[ সমান সমান উচ্চতাবিষ্ট বলিয়া সামান্তরিকগুলি একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত ] এখন, উপপাদ্য 29 এর ন্যায় প্রমাণ কর।]
অনুসিদ্ধান্ত 2. সমান সমান ভূমির উপর একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত সামান্তরিকের ক্ষেত্রফল পরস্পর সমান।
[ Parallelograms on equal bases and between the same parallels are equal in area.]
[ উপরিপাতন দ্বারা দুইটি সামান্তরিককে একই ভূমিবিশিষ্ট করিয়া উপপাদ্য 29 এর ন্যায় প্রমাণ কর। ]
অনুসিদ্ধান্ত 3. সমান সমান ভূমি ও সমান সমান উচ্চতাবিষ্ট সামান্তরিকের ক্ষেত্রফল পরস্পর সমান।
[ Parallelograms on equal bases and of equal altitudes are equal in area. ]
[ উপরিপাতন দ্বারা দুইটি সামান্তরিককে একই ভূমিবিশিষ্ট কর। উচ্চতা সমান বলিয়া উহারা একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত [অনু.114 (b)]। এখন, উপপাদ্য 29 এর ন্যায় প্রমাণ কর। ]
116. সামান্তরিকের ক্ষেত্রফল।
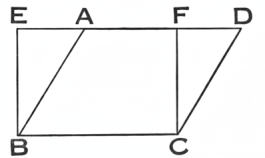
ABCD একটি সামান্তরিক; উহার ক্ষেত্রফল নির্ণয় করিতে হইবে।BCর উপর BE ও CF লম্ব টান। উহারা যেন যথাক্রমে বর্ধিত DAর সহিত E বিন্দুতে এবং ADর সহিত F বিন্দুতে মিলিত হইল।
এখন, ABCD সামান্তরিক এবং EBCF আয়ত একই ভূমি BCর উপর এবং একই BC ও ED সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত।
∴ ABCD সামান্তরিকের ক্ষেত্রফল = EBCF আয়তের ক্ষেত্রফল
= BC × CF ;
∴ সামান্তরিকের ক্ষেত্রফল = ভূমি × উন্নতি
∴ সামান্তরিকের ক্ষেত্রফল ÷ ভূমি = উন্নাতি এবং সামান্তরিকের ক্ষেত্রফল ÷ উচ্চতা = ভূমি।
অনুশীলনী 59
1. একটি সামান্তরিকের ভূমি 4.5 সেমি এবং উচ্চতা 3.2 সেমি; উহার ক্ষেত্রফল কত?
2. একটি সামান্তরিকের ক্ষেত্রফল 14 বর্গইঞ্চি এবং ভূমি 5.6ইঞ্চি; উহার উচ্চতা কত?
3. একটি আয়তক্ষেত্রের দৈর্ঘ্য 7.2সেমি এবং প্রস্থ সেমি; উহার সমান ক্ষেত্রফলবিশিষ্ট বর্গক্ষেত্রের বাহুর পরিমাপ কত?
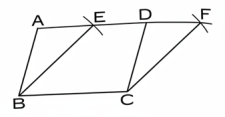4. একটি নির্দিষ্ট সামান্তরিকের সমান ক্ষেত্রফলবিশিষ্ট করিয়া একই ভূমির উপর একটি রম্বস আঁক। কিরূপ স্থলে অঙ্কন–কার্য অসম্ভব হইবে?
ABCD যেন নির্দিষ্ট সামান্তরিক। B ও C কে কেন্দ্র করিয়া এবং ভূমি BC কে ব্যাসার্ধ লইয়া দুইটি চাপ আঁক, যাহারা AD ও বর্ধিত AD কে যথাক্রমে E ও F বিন্দুতে কাটিল।EBCF উদ্দিষ্ট রম্বস হইবে। ক্ষুদ্রতর বাহুকে ভূমি ধরিলে অঙ্কন–কার্য অসম্ভব হইবে।
5. একটি নির্দিষ্ট আয়তের সমান ক্ষেত্রফলবিশিষ্ট করিয়া একই ভূমির উপর একটি রম্বস অঙ্কন কর।
[ প্রশ্ন 4 এর অঙ্কন–প্রণালী গ্রহণ কর। ]
6. কোন সরলরেখার উপর অঙ্কিত বর্গক্ষেত্রের সরলরেখাটির অর্ধেকের উপর অঙ্কিত বর্গক্ষেত্রের চারি গুণ।
[ The square on a straight line is four times the square on half the straight line. ]
7. কোন সরলরেখার উপর অঙ্কিত বর্গক্ষেত্রের সরলরেখাটির এক–তৃতীয়াংশের উপর অঙ্কিত বর্গক্ষেত্রের নয় গুণ।
8. একই ভূমি এবং সমান উচ্চতাবিষ্ট সামান্তরিকগুলির মধ্যে আয়তক্ষেত্রটির পরিসীমা ক্ষুদ্রতম।
[ Of the parallelograms on the same base and of equal altitudes, the rectangle has the least perimeter.]
[ ইঙ্গিত: সমকোণী ত্রিভুজের অতিভুজ অপেক্ষা অপর প্রত্যেক বাহু ক্ষুদ্রতর। ]
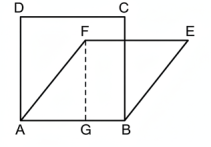9. একই ভূমির উপর অবস্থিত একটি বর্গক্ষেত্র ও একটি রম্বসের মধ্যে কোনটির ক্ষেত্রফল বৃহত্তর?
AB ভূমির উপর অবস্থিত ABCD একটি বর্গক্ষেত্র এবং ABEF একটি রম্বস। FG, রম্বসটির উচ্চতা।
প্রমাণ। ABCD বর্গক্ষেত্র = AB.AD
= AB.AF
এবং ABEF রম্বস = AB.FG;
কিন্তু AFG সমকোণী ত্রিভুজের অতিভুজ AF > FG,
∴ ABCD বর্গক্ষেত্র > ABEF রম্বস।
117. একটি ত্রিভুজ ও একটি আয়ত একই ভূমির উপর এবং একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত থাকিলে, উহাদের ক্ষেত্রফলের পরস্পর সম্বন্ধ নির্ণয়।
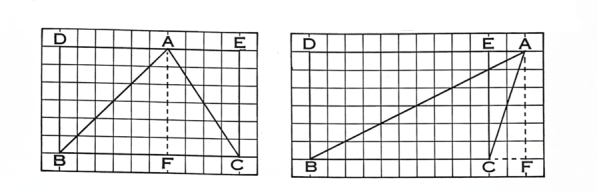
প্রথম চিত্র দ্বিতীয় চিত্র
ছক–কাগজে চিত্রর ন্যায় একই ভূমি BCর উপর এবং একই BC ও DE সমান্তরাল সরলরেখাদ্বয়ের মধ্যে ABC ত্রিভুজ এবং DBCE আয়ত আঁক। একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত বলিয়া উহারা একই উচ্চতাবিষ্ট। BC বা বর্ধিত BCর উপর AF লম্ব টান। তাহা হইলে, AF উভয়য়ের একই উচ্চতা।
প্রথম চিত্রে △ABC = △ABF + △AFC
= ½BF.AF + ½FC.AF
= ½ × .6 × .6 ব. ই. + ½ × .4 × .6 ব. ই.
= ½ × .6 (.6 + .4) ব. ই. = .3 ব. ই.
দ্বিতীয় চিত্রে △ABC = △ABF – △AFC = ½BF.AF – ½CF.AF
= ½ × 1.2 × .6 ব. ই. – ½ × .2 × .6 ব. ই.
= ½ × .6 (1.2 – .2) ব. ই. = .3 ব. ই.
উভয় চিত্রে ▭DBCE = BC.AF = 1 × .6 ব. ই. = .6 ব. ই.
ABC ত্রিভুজের ক্ষেত্রফল উভয় চিত্রেই DBCE আয়তের অর্ধেক হইল। অতএব সিদ্ধান্ত হইল:
সিদ্ধান্ত। একটি ত্রিভুজ ও একটি আয়ত একই ভূমির উপর এবং একই সমান্তরাল সরলরেখাদ্বয়ের মধ্যে অবস্থিত (অথবা একই উচ্চতাবিষ্ট) হইলে ত্রিভুজটির ক্ষেত্রফল আয়তটির ক্ষেত্রফলের অর্ধেক।
প্রশ্ন। ভূমি যথাক্রমে 8″, 11″, 13″, 1.5″ ও 1.6″ এবং উচ্চতা যথাক্রমে 7″, 9″, 1″.2″ ও 1″.5″ লইয়া ছক–কাগজে একটি করিয়া ত্রিভুজ ও আয়ত আঁক। প্রত্যেক স্থলে ত্রিভুজটির ক্ষেত্রফল আয়তটির ক্ষেত্রফলের অর্ধেক কিনা পরীক্ষা করিয়া দেখ।
